Содержание
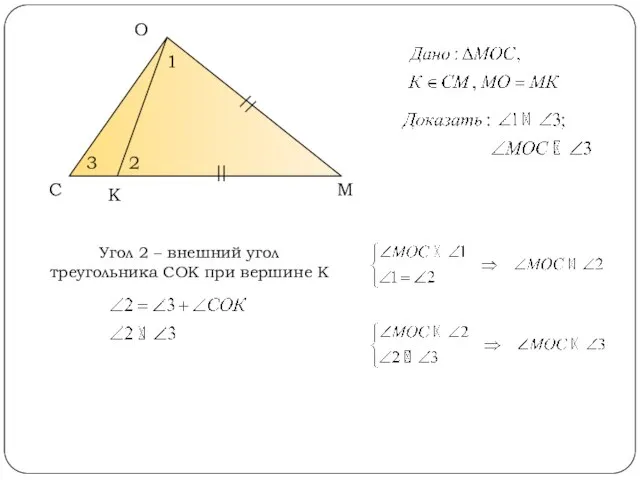
- 2. С О М К 3 2 1 Угол 2 – внешний угол треугольника СОК при вершине
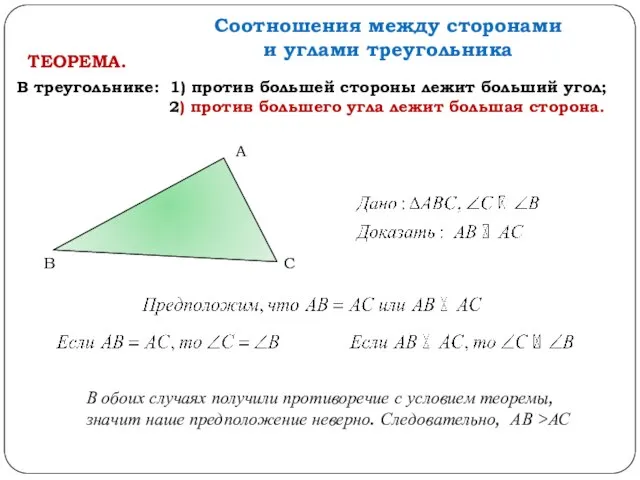
- 3. Соотношения между сторонами и углами треугольника В треугольнике: 1) против большей стороны лежит больший угол; 2)
- 4. Соотношения между сторонами и углами треугольника В треугольнике: 1) против большей стороны лежит больший угол; 2)
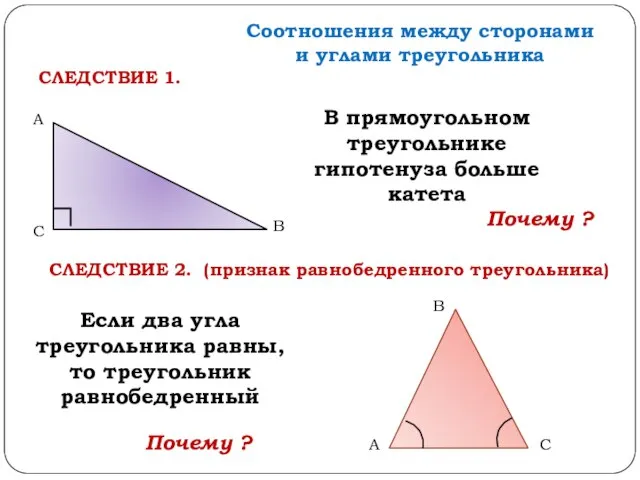
- 5. Соотношения между сторонами и углами треугольника В прямоугольном треугольнике гипотенуза больше катета СЛЕДСТВИЕ 1. В С
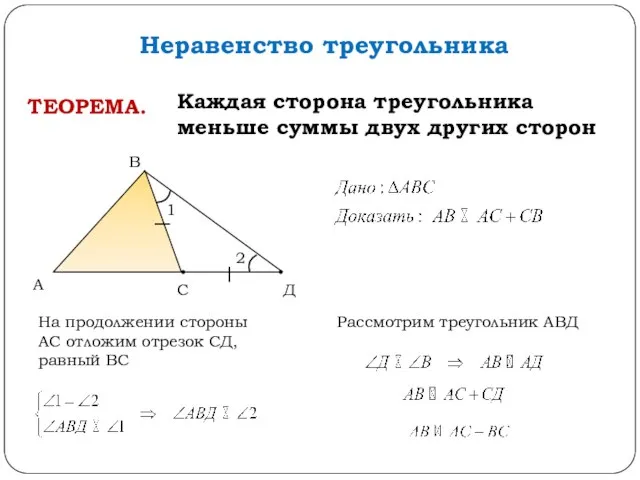
- 6. Неравенство треугольника ТЕОРЕМА. Каждая сторона треугольника меньше суммы двух других сторон С А В Д На
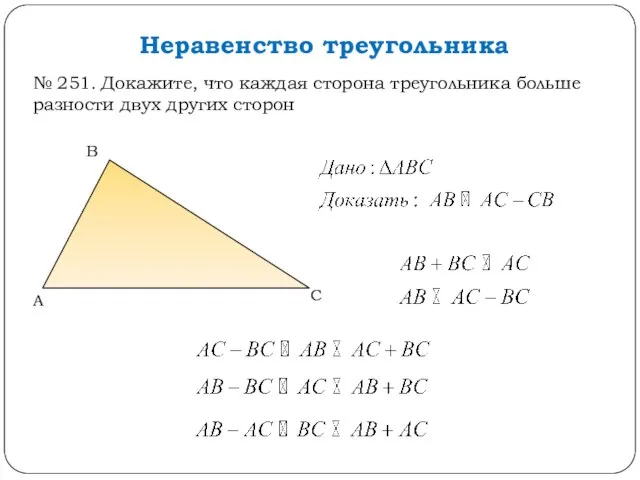
- 7. Неравенство треугольника № 251. Докажите, что каждая сторона треугольника больше разности двух других сторон С А
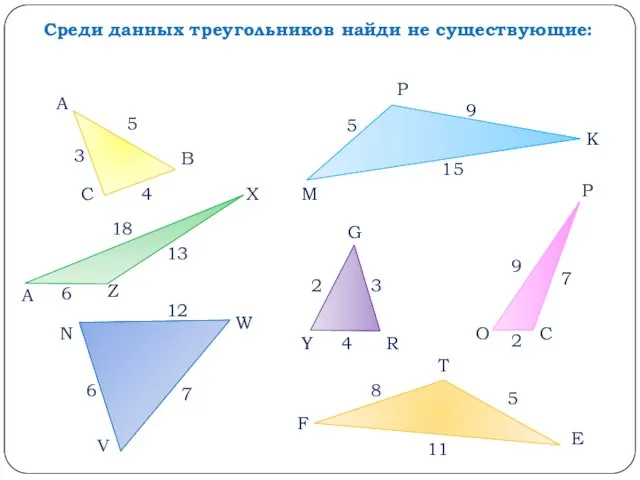
- 8. Среди данных треугольников найди не существующие: А В С М Р К Р С О G
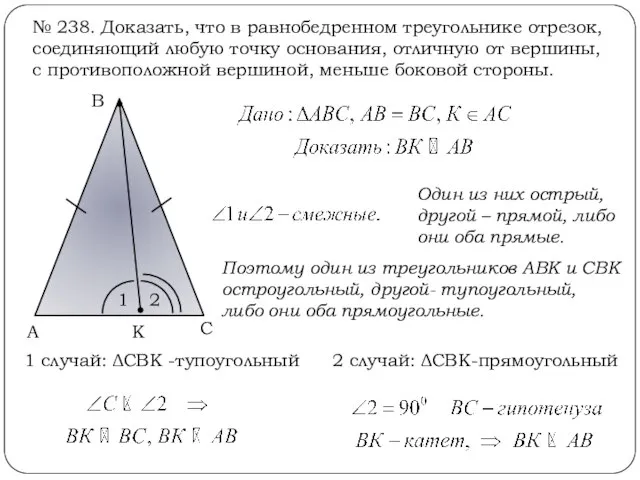
- 9. № 238. Доказать, что в равнобедренном треугольнике отрезок, соединяющий любую точку основания, отличную от вершины, с
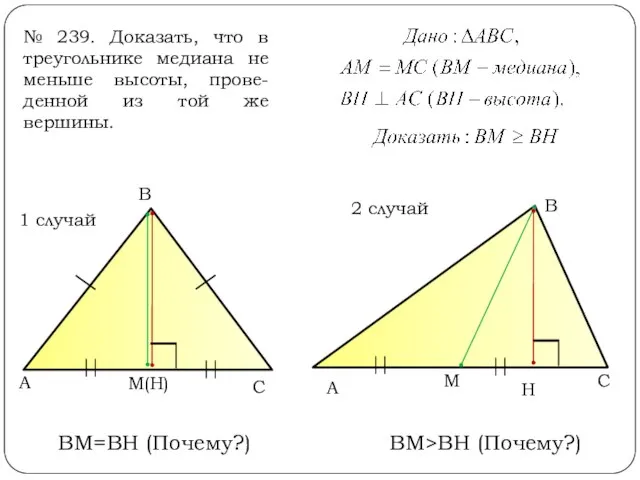
- 10. № 239. Доказать, что в треугольнике медиана не меньше высоты, прове-денной из той же вершины. А
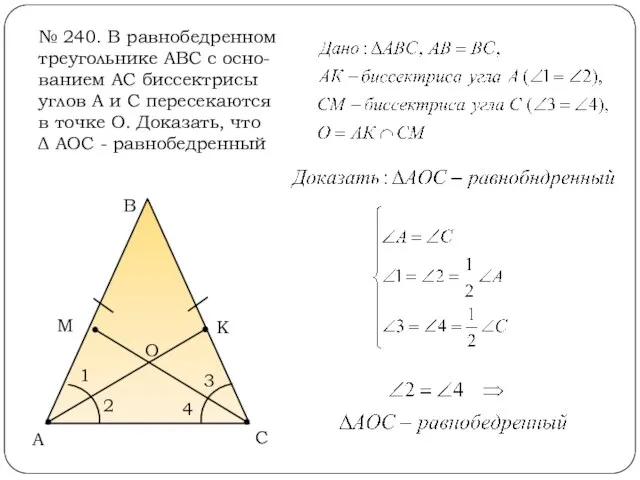
- 11. № 240. В равнобедренном треугольнике АВС с осно-ванием АС биссектрисы углов А и С пересекаются в
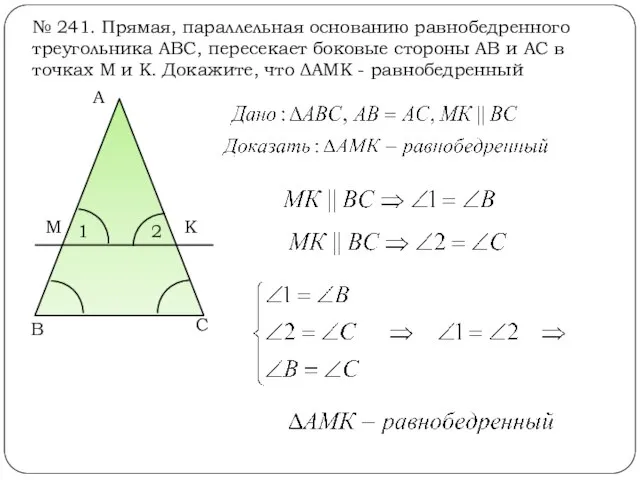
- 12. № 241. Прямая, параллельная основанию равнобедренного треугольника АВС, пересекает боковые стороны АВ и АС в точках
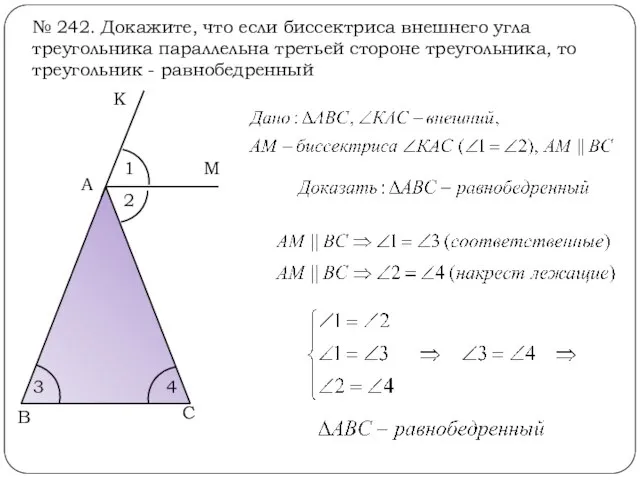
- 13. № 242. Докажите, что если биссектриса внешнего угла треугольника параллельна третьей стороне треугольника, то треугольник -
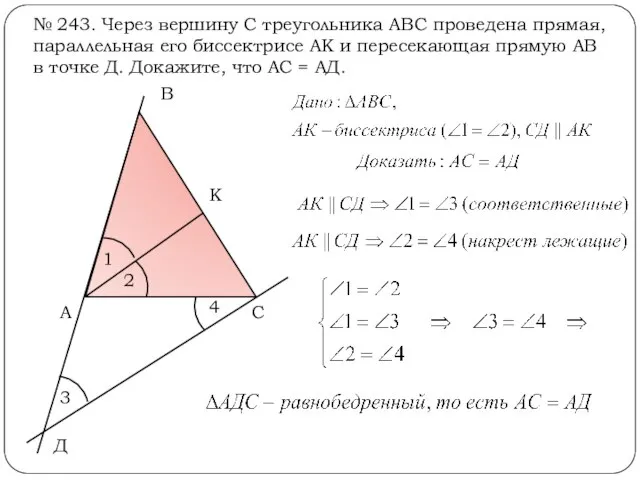
- 14. № 243. Через вершину С треугольника АВС проведена прямая, параллельная его биссектрисе АК и пересекающая прямую
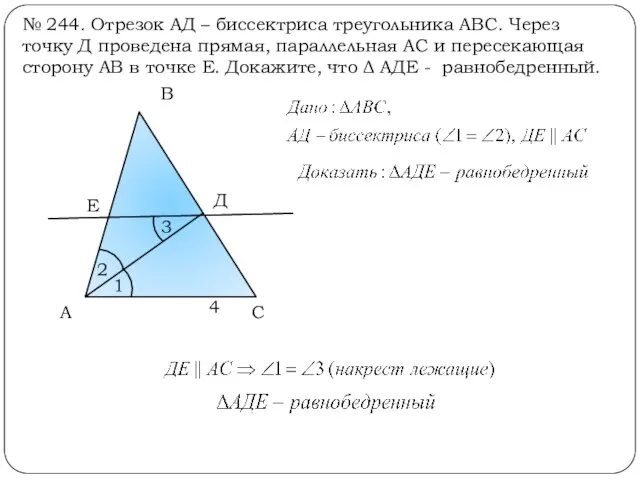
- 15. № 244. Отрезок АД – биссектриса треугольника АВС. Через точку Д проведена прямая, параллельная АС и
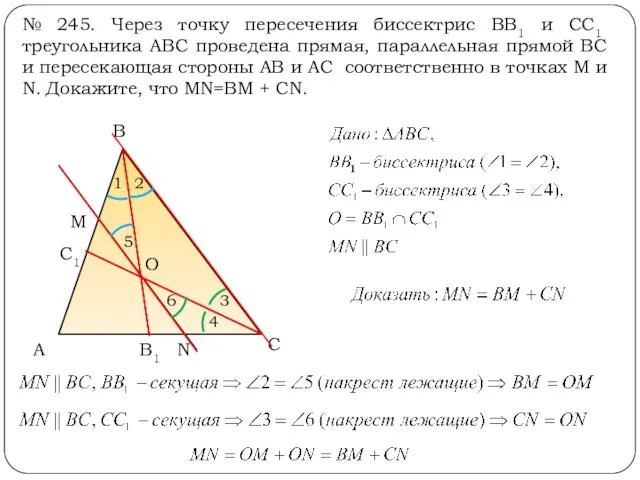
- 16. № 245. Через точку пересечения биссектрис ВB1 и СC1 треугольника АВС проведена прямая, параллельная прямой ВС
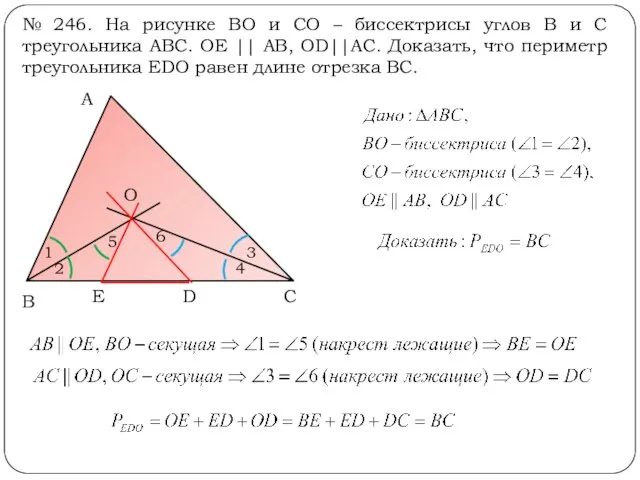
- 17. № 246. На рисунке ВО и СО – биссектрисы углов В и С треугольника АВС. OE
- 19. Скачать презентацию

 Презентация на тему Деление многозначного числа на однозначное
Презентация на тему Деление многозначного числа на однозначное  Графическое представление газовых законов
Графическое представление газовых законов Решение целых уравнений. 9 класс
Решение целых уравнений. 9 класс Построение графиков функций при решении квадратных уравнений
Построение графиков функций при решении квадратных уравнений Взаимное расположение прямых и плоскостей
Взаимное расположение прямых и плоскостей Тренажёр. Табличное умножение
Тренажёр. Табличное умножение Сфера и шар
Сфера и шар Граф – набор точек, некоторые из которых соединены линиями
Граф – набор точек, некоторые из которых соединены линиями Спин и расширенное супервремя
Спин и расширенное супервремя Значение степени возведение в степень
Значение степени возведение в степень Анализ геометрической формы предмета
Анализ геометрической формы предмета Эндогенность. Инструментальные переменные
Эндогенность. Инструментальные переменные Свойства функций . 9 класс
Свойства функций . 9 класс Решение задач на проценты
Решение задач на проценты Уравнение. Правила решения уравнения
Уравнение. Правила решения уравнения Стереометрия 1. ЕГЭ
Стереометрия 1. ЕГЭ Знакомая незнакомка. Парабола
Знакомая незнакомка. Парабола Сложение и вычитание в пределах 100
Сложение и вычитание в пределах 100 Степенная функция. Определение
Степенная функция. Определение Сумма углов треугольника
Сумма углов треугольника Уравнение прямой
Уравнение прямой Основные правила построения сечений
Основные правила построения сечений Графики степенных функций
Графики степенных функций Степенная функция
Степенная функция Неопределённый интеграл. Элементы интегрального исчисления
Неопределённый интеграл. Элементы интегрального исчисления Решение систем линейных уравнений при помощи компьютерных технологий
Решение систем линейных уравнений при помощи компьютерных технологий Тренировка интеллекта
Тренировка интеллекта Презентация на тему Степень с рациональным показателем (9 класс)
Презентация на тему Степень с рациональным показателем (9 класс)