Понятие функции и ее графика

Понятие функции и ее графика.

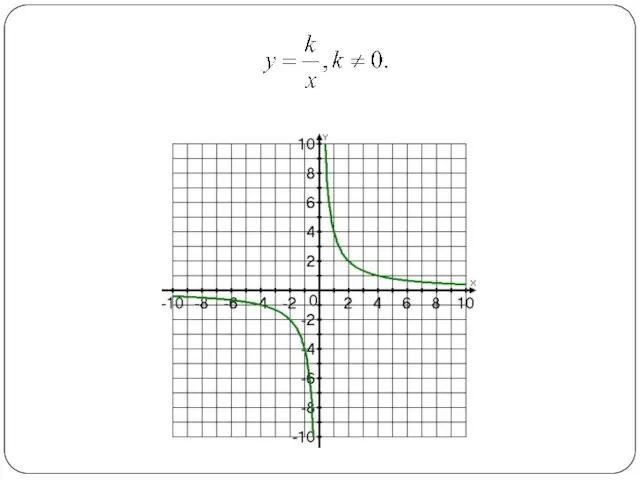
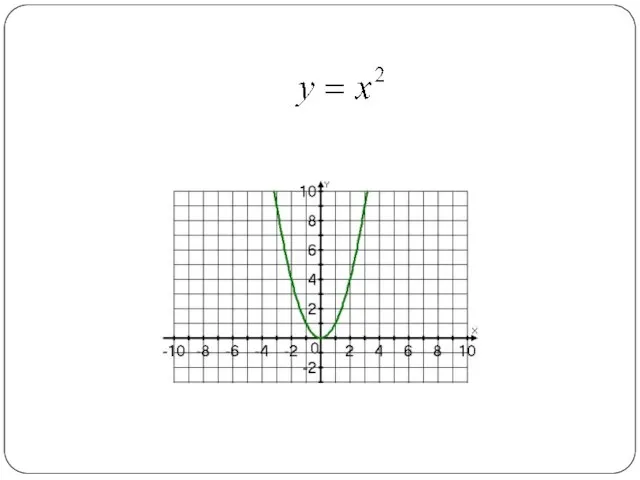
Сопоставьте графики функций и задающих их формул.

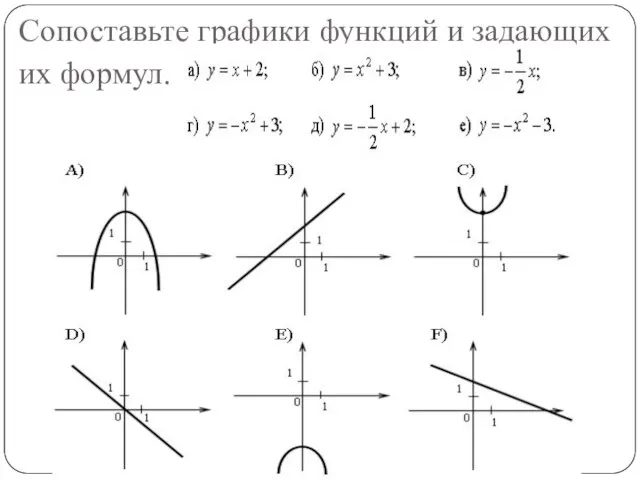
Определение
Функцией называют такую зависимость переменной y от переменной x, при которой каждому значению переменной x соответствует единственное значение переменной y.

Основные понятия
Переменную x называют независимой переменной или аргументом.
Переменную y называют зависимой переменной.
Переменная y является функцией от переменной x.
Значения зависимой переменной называют значениями функции.

Определение.
Все значения независимой переменной образуют область определения функции.
Все значения, которые принимает зависимая переменная, образуют область значений функции.

Определение
Если зависимость переменной y от переменной x является функцией, то коротко это записываю так:
y = f(x).

Определение.
Пусть дано некоторое множество Х и пусть в силу некоторого вполне определенного закона (f) каждому числу х из множества Х ставиться в соответствие одно вполне определенное число у, тогда говорят, что на Х задана функция y = f(x)
Множество Х называют областью определения функции y = f(x). Обозначают D (f).
Множество всех значений зависимой переменной у называют областью изменения функции y = f(x). Обозначают Е (f).

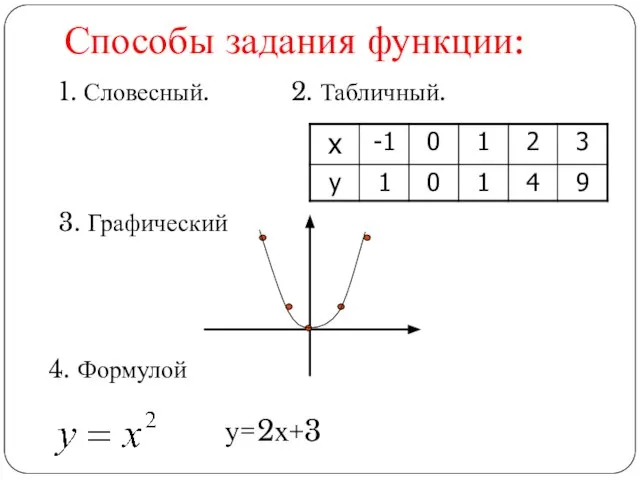
Способы задания функции:
1. Словесный.
2. Табличный.
3. Графический
4. Формулой
у=2х+3

Графиком функции y = f (x) называют множество всех точек координатной плоскости хОу вида (х; f(x)), где х – любое число из области определения функции.

Если график функции y = f(x) на некотором промежутке есть непрерывная линия, то функцию называют непрерывной на этом промежутке.
** функцию называют непрерывной на промежутке, если она определена в каждой точке этого промежутка и малому значению аргумента соответствует малое значение функции