Элементы математической логики

Высказывания
Предложение, о котором имеет смысл говорить, что оно является истинным или ложным, называют высказыванием.
Являются ли высказываниями предложения?
Волга впадает в Черное море.
2+2=4
Который час?
Мойте руки перед едой!
Земля – единственная обитаемая планета во Вселенной.

Значение истинности высказывания

Элементарные и сложные высказывания
Если никакая часть высказывания сама по себе не является высказыванием, то высказывание называют элементарным или исходным.
Сложным называют высказывание, допускающее разделение его на другие высказывания.

Операции над высказываниями
1. Инверсия ( логическое отрицание)
2. Дизъюнкция (логическое сложение)
3. Конъюнкция (логическое умножение)
4. Импликация (логическое следствие)
5. Эквивалентность (логическое равенство)

Обозначения и значение

Основные законы логики
1. Закон тождества
2. Закон непротиворечия
3. Закон исключения третьего
4. Закон отрицания отрицания

Закон тождества
Всякое высказывание тождественно са­мому себе:
А = А

Закон непротиворечия

Закон исключения третьего

Закон отрицания отрицания

Пример задачи
Трое подозреваемых в преступлении Иванов, Петров и Сидоров дали следующие показания:
Иванов сказал: «Если виновен Сидоров, то и Петров тоже виновен».
Петров сказал: «Виновен либо Иванов, либо Сидоров, но не оба».
Сидоров сказал: «Я не виновен, а виновен Петров».

Построить таблицу истинности каждого высказывания и по ней определить:
а) Кто виновен, если все говорят правду?
б) Кто виновен, если все лгут? в) Кто лжет, если все виновны?
г) Кто лжет, если все невиновны?
д) Кто виновен, если виновные лгут, а невиновные говорят правду?

Введем простые высказывания: А={виновен Иванов};
В={виновен Петров};
С={виновен Сидоров}.

Составляем таблицу истинности каждого высказывания:

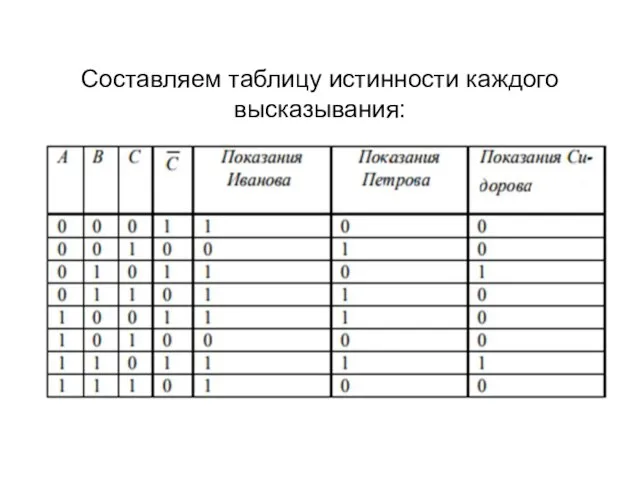
а) Если все говорят правду, то в показаниях (последние три столбца) должны быть три единицы. Такому условию соответствует предпоследняя строка, из которой по значениям в первых трех столбцах (1,1,0) делаем вывод, что Иванов и Петров виновны, а Сидоров нет.

б) Если все лгут, то в показаниях должны быть три нуля. Такому условию соответствует шестая строка, из которой по значениям в первых трех столбцах делаем вывод, что Иванов и Сидоров виновны, а Петров нет.

в) Условию того, что все виновны, соответствует последняя строка, у которой в первых трех столбцах все единицы. По значениям показаний (последние три столбца) видно, что Иванов говорит правду, а Петров и Сидоров лгут

г) Условию того, что все невиновны, соответствует первая строка, у которой в первых трех столбцах все нули. По значениям показаний видно, что Иванов говорит правду, а Петров и Сидоров лгут.