Содержание
- 2. ─ матрица коэффициентов ─ столбец неизвестных ─ столбец свободных членов ─ расширенная матрица коэффициентов
- 3. ─ матричная форма записи системы ─ операторная форма записи системы
- 4. Решением системы называется совокупность n чисел при подстановке которых все уравнения системы обращаются в верные равенства.
- 5. Теорема 1 (Кронекера-Капелли). Система линейных уравнений совместна тогда и только тогда, Система линейных уравнений совместна тогда
- 6. Теорема 2. Если ранг матрицы коэффициентов совместной системы равен количеству неизвестных, Теорема 3. Если ранг матрицы
- 7. Пример. Найти количество решений системы Решение. Значит, т.е. система не имеет решений.
- 8. п.2. Решение СЛУ. Рассмотрим систему Пусть
- 9. (1) Решение системы по формуле (1) называют матричным способом. Так как , то существует обратная матрица
- 10. Пример. Решение.
- 12. Правило Крамера Используя формулу для нахождения обратной матрицы формулу (1) перепишем в виде: или
- 13. Значит, Рассмотрим определитель Применив теорему Лапласа, разложим его по элементам первого столбца: Тогда
- 14. Аналогично, Формулы называются формулами Крамера.
- 15. Пример.
- 17. Метод Гаусса Рассмотрим систему Процесс решения состоит из двух этапов: 1) прямой ход; 2) обратный ход.
- 18. 1) Прямой ход. Задача: привести систему к ступенчатому виду 1-й шаг. Пусть в системе (2) (иначе
- 19. Умножим 1-е уравнение на и сложим со 2-м. Умножим 1-е уравнение на и сложим с 3-м
- 20. Получим систему Аналогично исключим неизвестную из всех уравнений кроме 1-го и 2-го. Продолжая таким образом, получим
- 21. Замечание 1. Если в прямом методе получается уравнение вида то его отбрасываем. Замечание 2. Если в
- 22. Замечание 3. Если в ступенчатой системе то система имеет единственное решение (см. теорему 2). Замечание 4.
- 23. 2) Обратный ход. Из последнего уравнения находим (или выражаем через остальные неизвестные). Подставляем в предпоследнее уравнение
- 24. Пример.
- 25. Прямой ход
- 27. Скачать презентацию























 Нулевой угловой коэффицент
Нулевой угловой коэффицент В стране математики
В стране математики Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Площади. Формула Пика
Площади. Формула Пика Функции многих переменных: частные производные, дифференциалы. Лекция 2
Функции многих переменных: частные производные, дифференциалы. Лекция 2 Первые уроки в 5 кассе
Первые уроки в 5 кассе Решение задач с помощью рациональных уравнений. 8 класс
Решение задач с помощью рациональных уравнений. 8 класс Таблица сложения
Таблица сложения Подготовка к ЕГЭ (профильный уровень). Теория вероятности
Подготовка к ЕГЭ (профильный уровень). Теория вероятности Элементы теории вероятности
Элементы теории вероятности График функции. Урок применения знаний и умений. Класс: 8
График функции. Урок применения знаний и умений. Класс: 8 Иррациональные уравнения
Иррациональные уравнения Смежные углы
Смежные углы Определение арифметического корня п-ой степени
Определение арифметического корня п-ой степени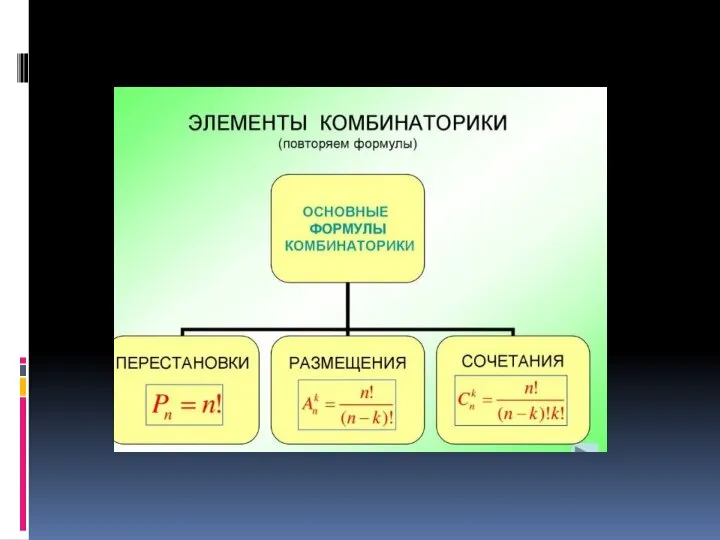 Основные понятия комбинаторики
Основные понятия комбинаторики Презентация на тему Буквенные выражения (2 класс)
Презентация на тему Буквенные выражения (2 класс) 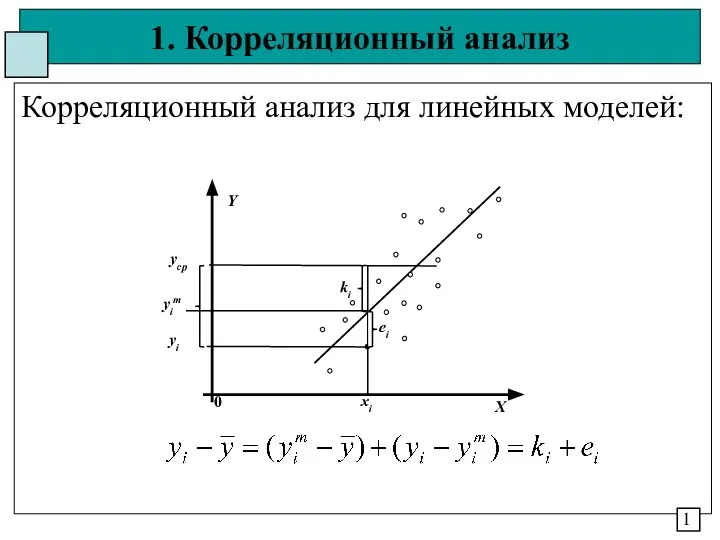 Корреляционный анализ для линейных моделей
Корреляционный анализ для линейных моделей Введение таблицы умножения (Школа XXI века. Рудницкая В.Н )
Введение таблицы умножения (Школа XXI века. Рудницкая В.Н ) Решение тригонометрических уравнений
Решение тригонометрических уравнений Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл Спиннеры и метематика
Спиннеры и метематика krivye-vtorogo-poryadka (1)
krivye-vtorogo-poryadka (1) Обратные матрицы
Обратные матрицы Сравнение моделей
Сравнение моделей Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Презентация на тему Многоугольники (1 класс)
Презентация на тему Многоугольники (1 класс)  Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром.
Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром. Перпендикулярность прямых в пространстве
Перпендикулярность прямых в пространстве