Содержание
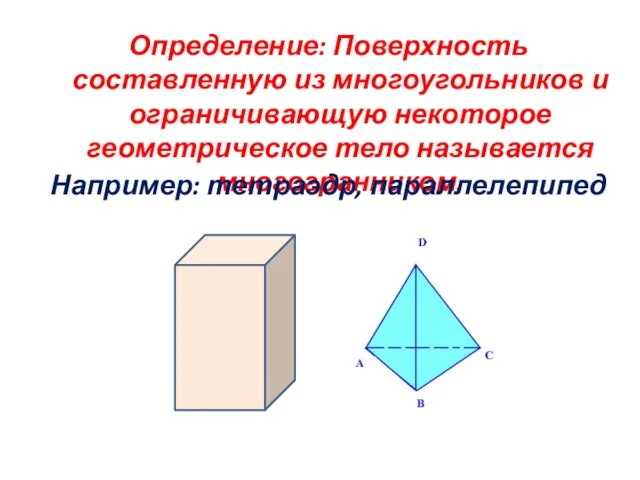
- 2. Определение: Поверхность составленную из многоугольников и ограничивающую некоторое геометрическое тело называется многогранником. Например: тетраэдр, параллелепипед
- 3. Они имеют вершины, ребра, грани, диагонали Определение: Отрезок соединяющий две вершины не принадлежащие одной грани называют
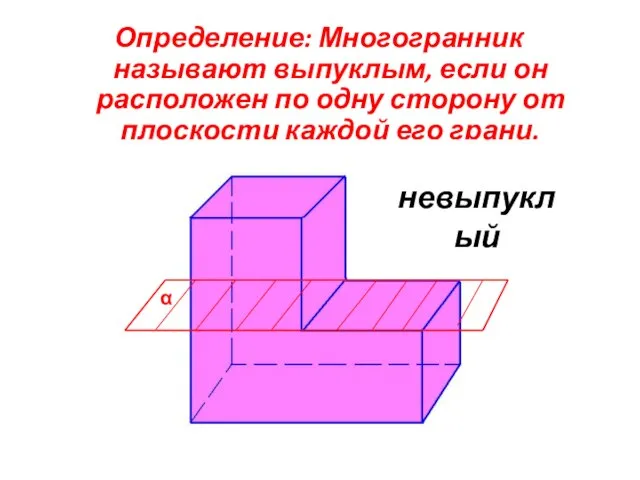
- 4. Определение: Многогранник называют выпуклым, если он расположен по одну сторону от плоскости каждой его грани. невыпуклый
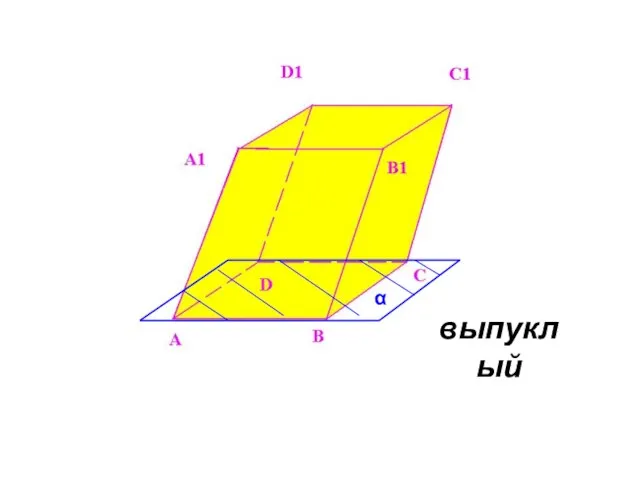
- 5. выпуклый
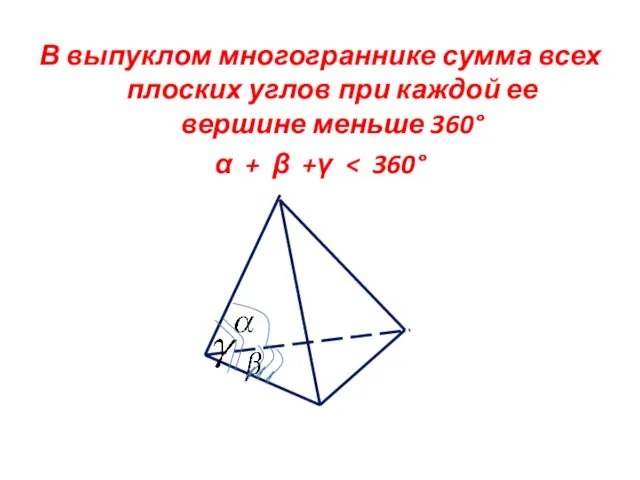
- 6. В выпуклом многограннике сумма всех плоских углов при каждой ее вершине меньше 360° α + β
- 7. Призма Евклид определяет призму как телесную фигуру, заключенную между двумя равными и параллельными плоскостями (основаниями) и
- 8. Призмы вокруг нас
- 9. Определение: Многогранник составленный из двух равных многоугольников расположенных в параллельных плоскостях и n- параллелограммов называется призмой.
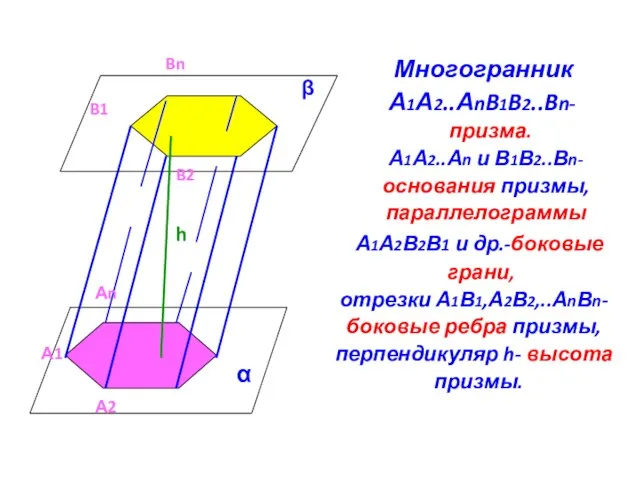
- 10. Многогранник А1А2..АnB1B2..Bn- призма. А1А2..Аn и В1В2..Вn- основания призмы, параллелограммы А1А2В2В1 и др.-боковые грани, отрезки А1В1,А2В2,..АnВn- боковые
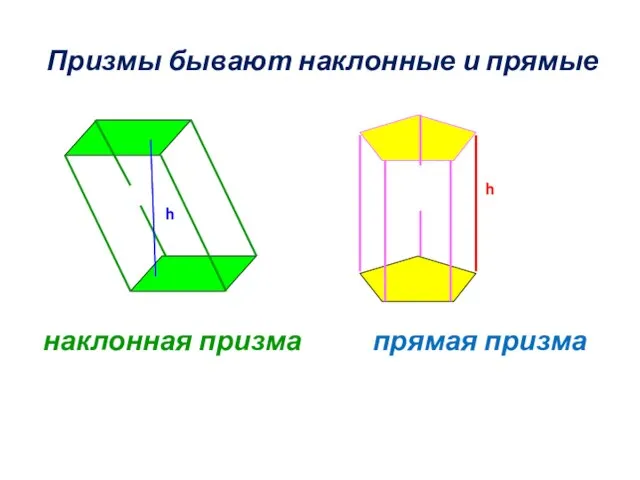
- 11. наклонная призма прямая призма Призмы бывают наклонные и прямые
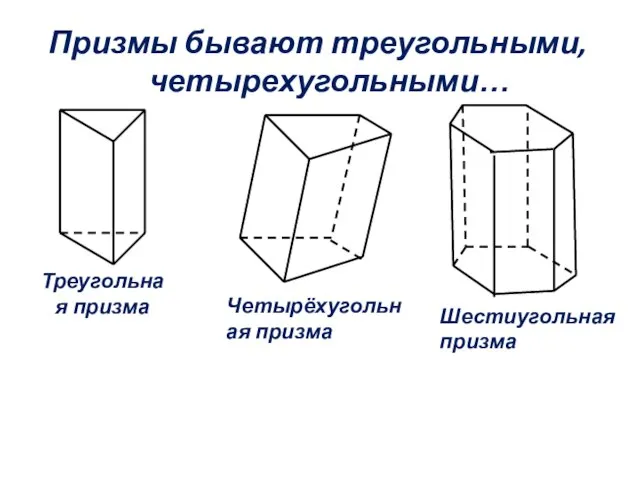
- 12. Треугольная призма Четырёхугольная призма Шестиугольная призма Призмы бывают треугольными, четырехугольными…
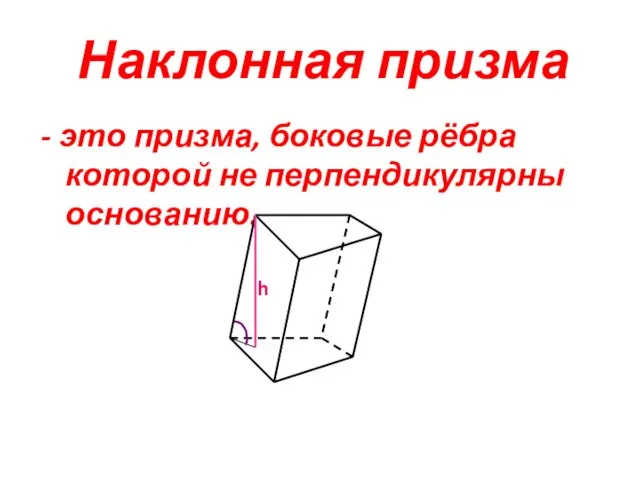
- 13. Наклонная призма - это призма, боковые рёбра которой не перпендикулярны основанию.
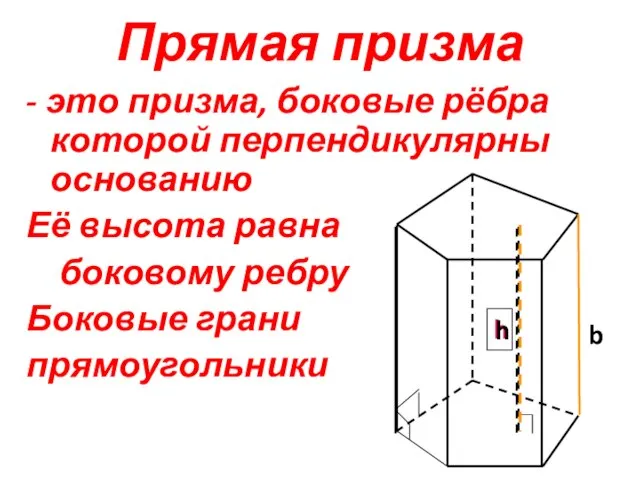
- 14. Прямая призма - это призма, боковые рёбра которой перпендикулярны основанию Её высота равна боковому ребру Боковые
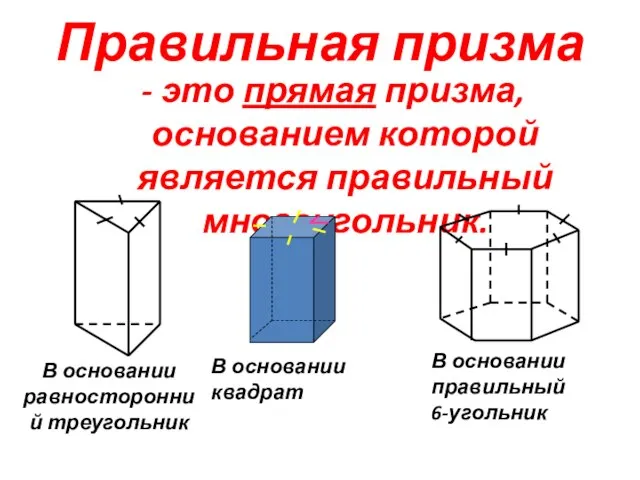
- 15. Правильная призма - это прямая призма, основанием которой является правильный многоугольник. В основании равносторонний треугольник В
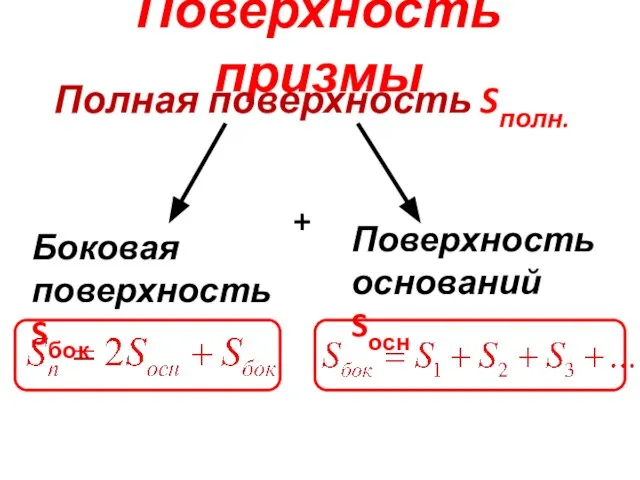
- 16. Поверхность призмы Полная поверхность Sполн. +
- 17. Боковая поверхность прямой призмы Теорема: Боковая поверхность прямой призмы равна произведению периметра основания на длину бокового
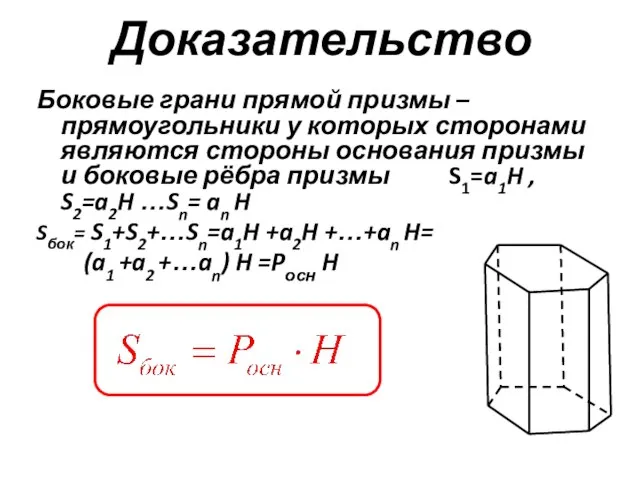
- 18. Доказательство Боковые грани прямой призмы – прямоугольники у которых сторонами являются стороны основания призмы и боковые
- 20. Скачать презентацию





 Золотое сечение в Web-дизайне
Золотое сечение в Web-дизайне Презентация на тему Число 0 Цифра 0
Презентация на тему Число 0 Цифра 0 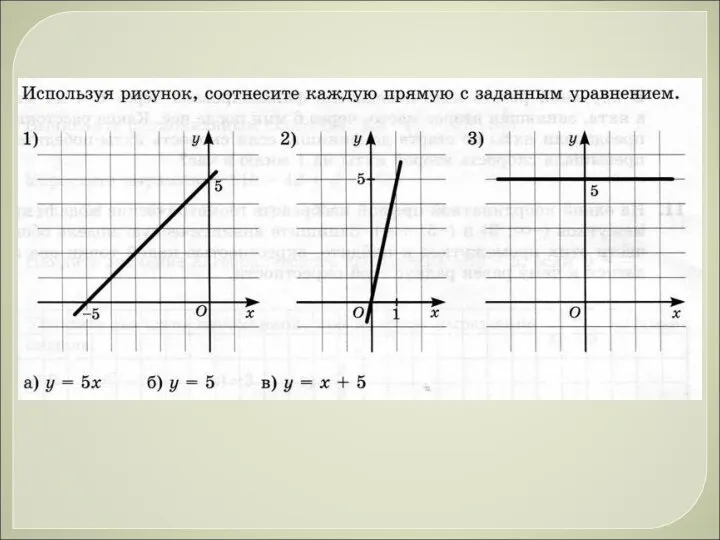 Соотношение прямой с заданным уравнением
Соотношение прямой с заданным уравнением Великие матекматики и их открытия
Великие матекматики и их открытия Взаимное расположение двух прямых в пространстве
Взаимное расположение двух прямых в пространстве Куб. Измерения куба
Куб. Измерения куба Временные ряды
Временные ряды Многогранники
Многогранники Кластерный анализ. Лекция 8
Кластерный анализ. Лекция 8 Область определения и множество значений тригонометрических функций
Область определения и множество значений тригонометрических функций Смежные и вертикальные углы
Смежные и вертикальные углы Задачи с цифрами 1, 5, 9
Задачи с цифрами 1, 5, 9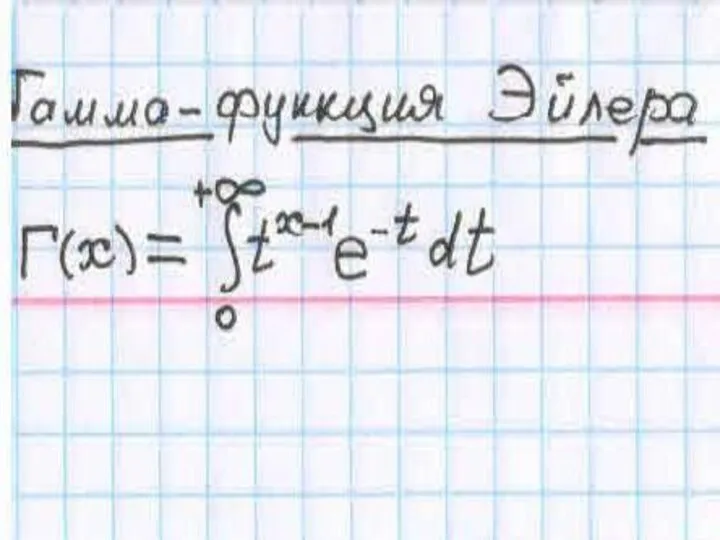 Гамма-функция Эйлера
Гамма-функция Эйлера Проценты (5)
Проценты (5) Восход и заход солнца с точки зрения графика тригонометрических функций
Восход и заход солнца с точки зрения графика тригонометрических функций Обобщающий урок по теме: параллелограм, прямоугольник, ромб, квадрат
Обобщающий урок по теме: параллелограм, прямоугольник, ромб, квадрат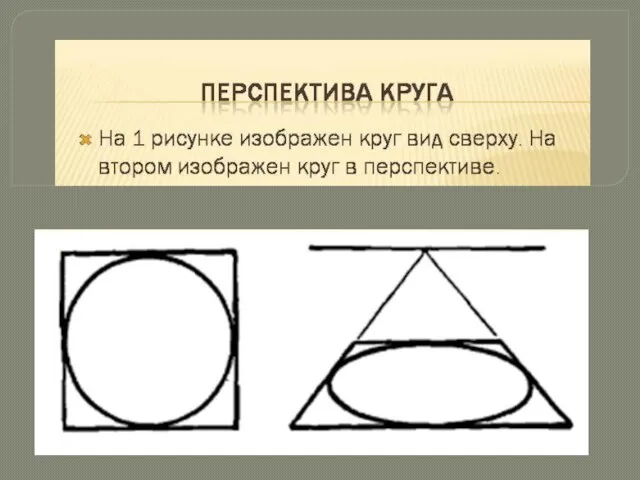 Перспектива круга
Перспектива круга Математика. Русский язык. Технология. Вопросы
Математика. Русский язык. Технология. Вопросы Частные производные. Лекция 17
Частные производные. Лекция 17 797821
797821 Число и цифра 5
Число и цифра 5 Понятие угла. Тригонометрические формулы
Понятие угла. Тригонометрические формулы Օբյեկտ-կողմնորոշված ծրագրավորման լեզու
Օբյեկտ-կողմնորոշված ծրագրավորման լեզու Компоненты вычитания
Компоненты вычитания теория вероятностей задачи
теория вероятностей задачи Пространственные векторы в асинхронном двигателе. Эйлер (1707-1783 гг)
Пространственные векторы в асинхронном двигателе. Эйлер (1707-1783 гг) Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Теория оптимальной фильтрации и управления. Лекция № 7 (3/2)
Теория оптимальной фильтрации и управления. Лекция № 7 (3/2)