Математика в специальности

Говорят, что математика – царица всех наук. Область применения математических законов не знает границ, они используются во многих отраслях науки и производства. В том числе, и для решения задач строительства.

Рассмотрим простые задачи, с которыми сталкивается буквально каждый строитель - практик – не только профессионал, но и любитель. И каждый этот строитель волей - неволей использует математику.

Одним из самых важных условий при постройке нового дома всегда было правильно разметить углы. Но как получить прямой угол? Ответ на этот вопрос дал греческий математик Пифагор, сформулировав и доказав свою известную теорему. С тех пор задача разметки углов в профессиональном строительстве решается именно через прямоугольный треугольник.

Еще одна строительная задача, при решении которой применяется математика – замер площадей сложной формы.

Допустим, у нас есть зал с большим количеством ниш, и в некоторых местах стены соприкасаются не под прямым углом. Мы хотим застелить пол зала ламинатом. Но чтобы заказать ламинат, нам необходимо знать площадь пола.
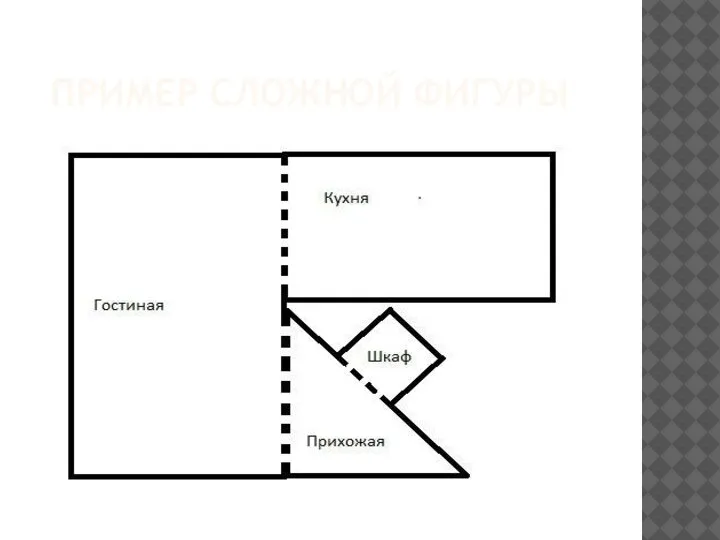
На первый взгляд, сложная задача. Но математика решает ее очень просто, путем разделения сложной фигуры на прямоугольники и треугольники.

ПРИМЕР СЛОЖНОЙ ФИГУРЫ

ДЛЯ ТОГО ЧТОБЫ ОПРЕДЕЛИТЬ ПЛОЩАДЬСЛОЖНОЙ ФИГУРЫ ЕЕ СЛЕДУЕТ РАЗБИТЬ НА ПРОСТЫЕ ПРОФИЛИ.

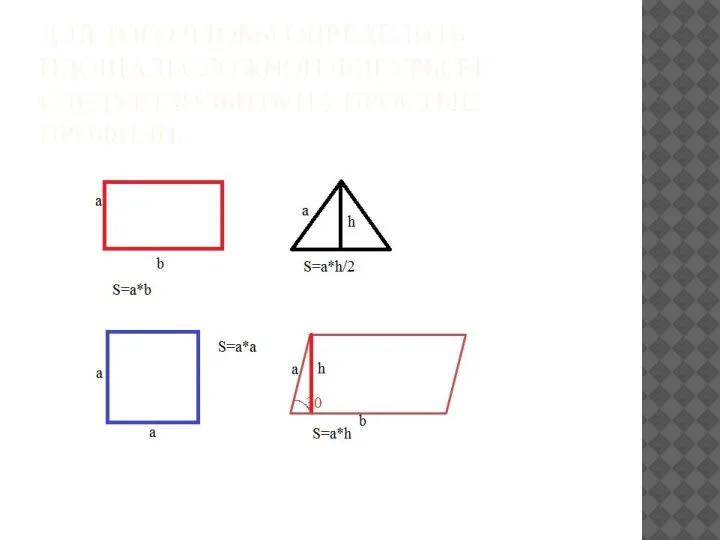
Так же математика применяется для расчетов самой разной сложности.
Qht=1.16хqhrhх(th-tc)kt
Математика применяется так же в расчете высоты здания, диаметре трубопровода, расчета отметок заложения трубопровода итд.

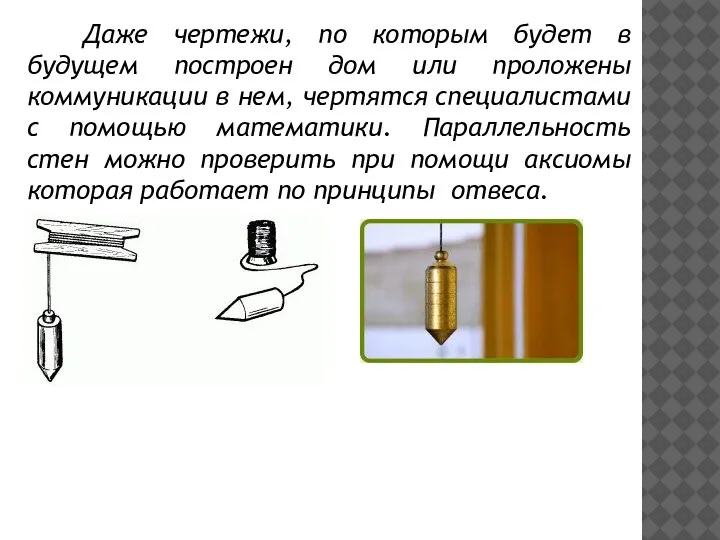
Даже чертежи, по которым будет в будущем построен дом или проложены коммуникации в нем, чертятся специалистами с помощью математики. Параллельность стен можно проверить при помощи аксиомы которая работает по принципы отвеса.

Таким образом без применения математики невозможно построить дом или провести в нем коммуникации.

ЗОЛОТОЕ СЕЧЕНИЕ
ЗОЛОТЫМ СЕЧЕНИЕМ и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей. На рисунке точка С делит отрезок АВ в отношении золотого сечения. Это отношение приближённо равно 0,68

Золотое сечение часто встречается в древних сооружения даре такое известное здание как Парфенон в Афинах построено с его помощью. Отношение высоты здания к его длине равно 0,618.

ДАЖЕ ЧЕЛОВЕК ПОДЧИНЕН ЗОЛОТОМУ СЕЧЕНИЮ
Никто не усомнился , что внешне человек построен симметрично: левой руке всегда соответствует правая и обе руки совершенно одинаковы. Но сходство между нашими руками, ушами, глазами и другими частями тела такое же ,как между предметом и его отражением в зеркале.