Планы второго порядка

Рассмотри наиболее часто употребляемые планы второго порядка.
Они отличаются:
− количеством опытов;
− расположением точек в факторном пространстве.
Чем больше точек в плане эксперименте, тем информативнее результаты и точнее уравнения регрессии, которые описывают объект исследований, но при этом существенно увеличивается объем экспериментальной работы.

.
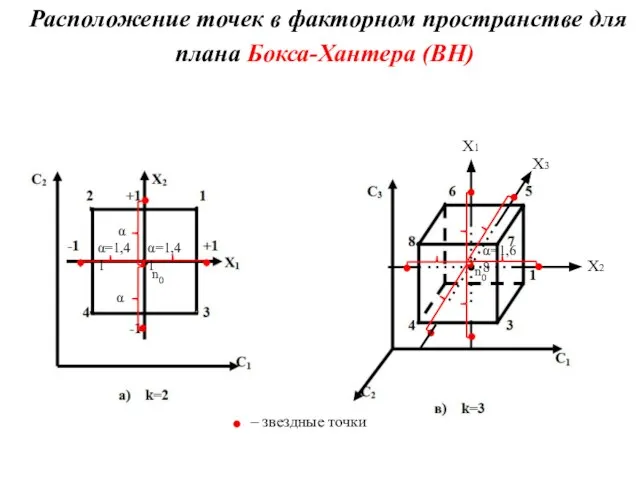
Планы Бокса-Хантера (ВН)
Планы Бокса-Хантера (ВН) включают:
− вершины гиперкуба;
− точки в центре области планирования;
− «звездные точки» − точки на осях факторов на расстоянии α от цента области планирования.
Число звездных точек определяется как 2∙k. Величина звездного плеча α определяется как α = 2k/4, где k –количество факторов.
Опыты в центре плана n0 повторяются многократно, т.к. при составлении плана, в том числе при выборе значений нулевых уровней (середин области определения факторов) предполагается, что эти нулевые уровни приблизительно соответствуют оптимальному сочетанию значений факторов.

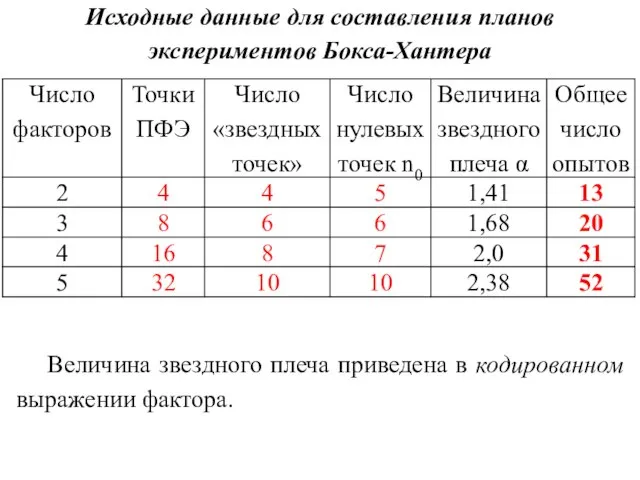
Исходные данные для составления планов экспериментов Бокса-Хантера
Величина звездного плеча приведена в кодированном выражении фактора.

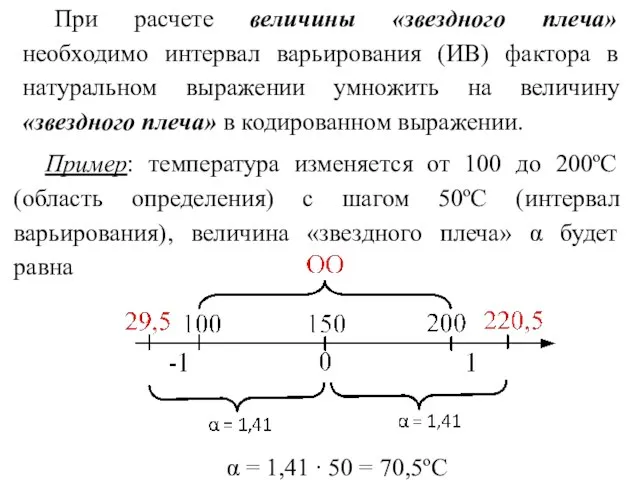
При расчете величины «звездного плеча» необходимо интервал варьирования (ИВ) фактора в натуральном выражении умножить на величину «звездного плеча» в кодированном выражении.
Пример: температура изменяется от 100 до 200ºС (область определения) с шагом 50ºС (интервал варьирования), величина «звездного плеча» α будет равна
α = 1,41 ∙ 50 = 70,5ºС

Для всех планов второго порядка целесообразно в соответствии с определением плана расположить точки в факторном пространстве, а затем последовательно вписать координаты точек в матрицу плана эксперимента.

Расположение точек в факторном пространстве для плана Бокса-Хантера (ВН)
α=1,41
α=1,41
α
α
n0
‒ звездные точки
Х1
Х3
Х2
n0
α=1,68

При использовании плана Бокса-Хантера необходимо следить за совместимостью факторов, т.к. звездные точки расширяют область определения факторов, и в некоторых точках продукция может быть просто не произведена (см. требование к факторам по совместимости).

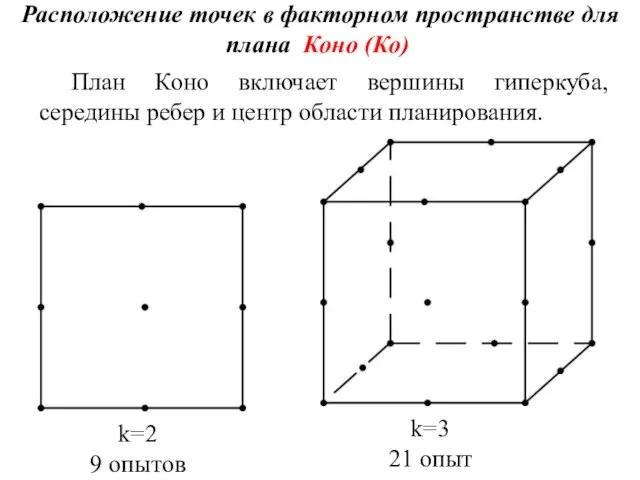
Расположение точек в факторном пространстве для плана Коно (Ко)
k=2
9 опытов
k=3
21 опыт
План Коно включает вершины гиперкуба, середины ребер и центр области планирования.

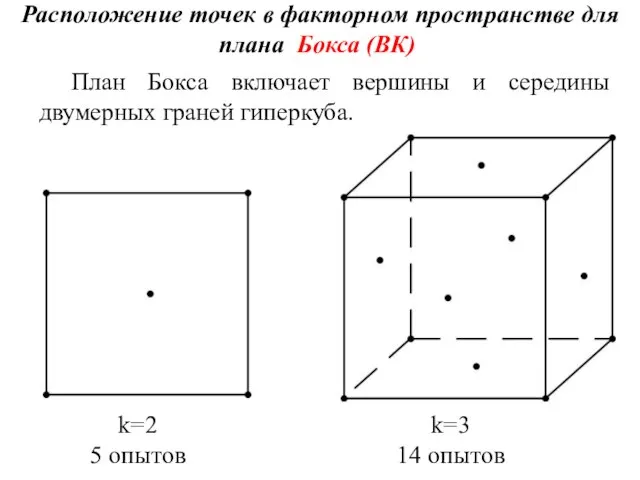
Расположение точек в факторном пространстве для плана Бокса (ВК)
План Бокса включает вершины и середины двумерных граней гиперкуба.
k=2
5 опытов
k=3
14 опытов

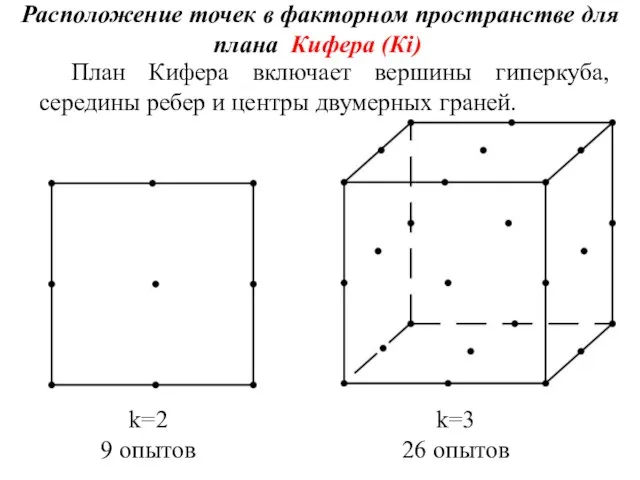
Расположение точек в факторном пространстве для плана Кифера (Кi)
План Кифера включает вершины гиперкуба, середины ребер и центры двумерных граней.
k=2
9 опытов
k=3
26 опытов

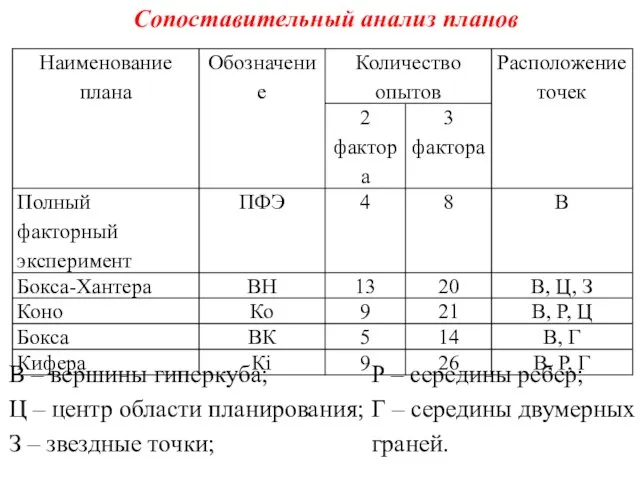
Сопоставительный анализ планов
В ‒ вершины гиперкуба;
Ц ‒ центр области планирования;
З ‒ звездные точки;
Р ‒ середины ребер;
Г ‒ середины двумерных
граней.

1) Полный факторный эксперимент (ПФЭ) применяется в тех случаях, где можно предположить с высокой степенью вероятности, что в исследуемой области, т.е. в области определения каждого фактора, все исследуемые показатели качества линейно зависят от факторов.
2) Планы Бокса-Хантера применяются в следующих случаях:
− если в результате ПФЭ были получены неадекватные (недостоверно описывающие технологический процесс) уравнения.
− если необходимо охватить достаточно широкую область факторного пространства, т.к. только в этих планах есть звездные точки. Но всегда следует оценивать в этих планах реализуемость сочетаний факторов в звездных точках, т.е. чтобы получение продукции вообще было возможным.

3) Планы Коно достаточно информативны и вместе с тем включают небольшое количество опытов, поэтому являются компромиссными с точки зрения затрат и информативности.
4) Планы Бокса наиболее экономичны среди планов 2-го порядка. Эти планы следует применять в тех случаях, когда экспериментальная работа очень трудоемка, требует много материальных и временных затрат.
5) Планы Кифера наиболее информативны, т.е. обеспечивают наиболее достоверную информацию об объекте исследования, но при этом наиболее трудоемкие.