Слайд 2Геометрические утверждения
Если две точки одной прямой лежат в плоскости, то и
вся прямая

лежит в этой плоскости.
Слайд 3Геометрические утверждения
Если две параллельные плоскости пересечены третьей, то
линии их пересечения параллельны.

Слайд 4Сечение куба плоскостью.
Задача1: Построить сечение куба плоскостью, которая проходит через точки K,

L, M, расположенные на его ребрах.
Слайд 5Дано:
ABCDА1B1C1D1 -куб,
точка К принадлежит ребру A1В1, точка L принадлежит
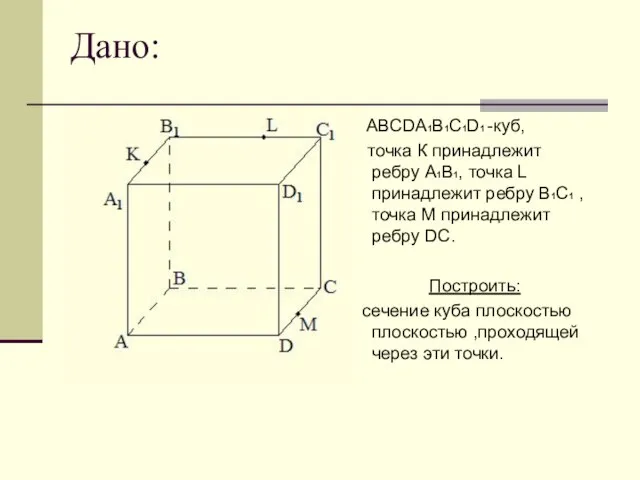
ребру В1C1 , точка М принадлежит ребру DC.
Построить:
сечение куба плоскостью плоскостью ,проходящей через эти точки.
Слайд 6Решение:
Проведем прямую КL и отметим точки ее пересечения с продолжениями соответствующих
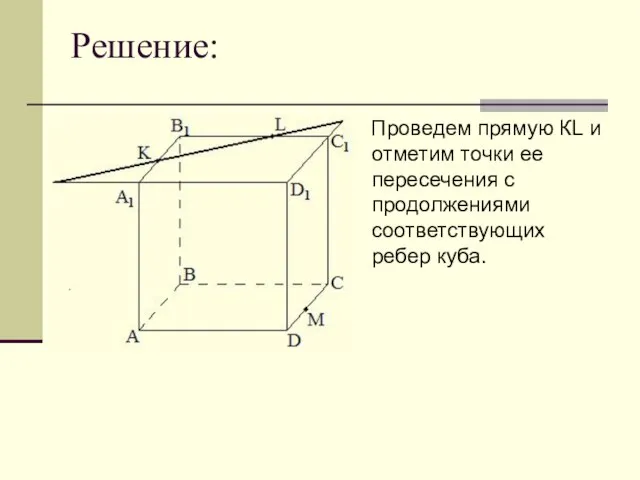
ребер куба.
Слайд 7 Получим еще две точки, лежащие в плоскости сечения и на продолжениях
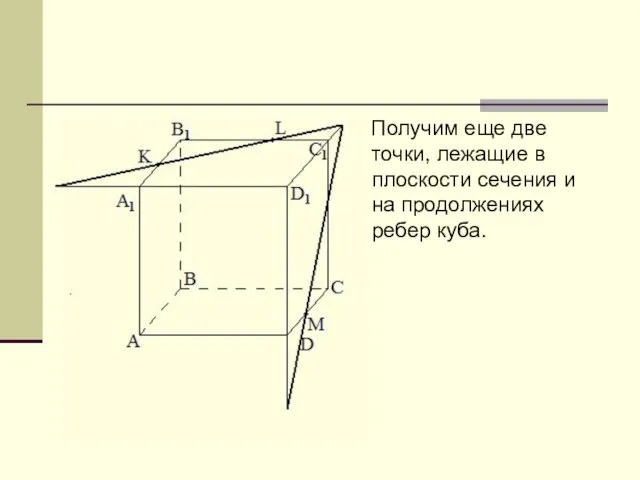
ребер куба.
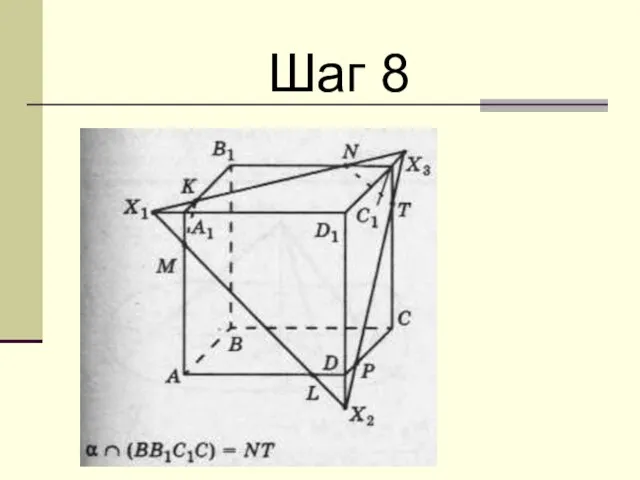
Слайд 8 Соединим точки ,лежащие в одной грани. Получим «следы» пересечения секущей плоскости
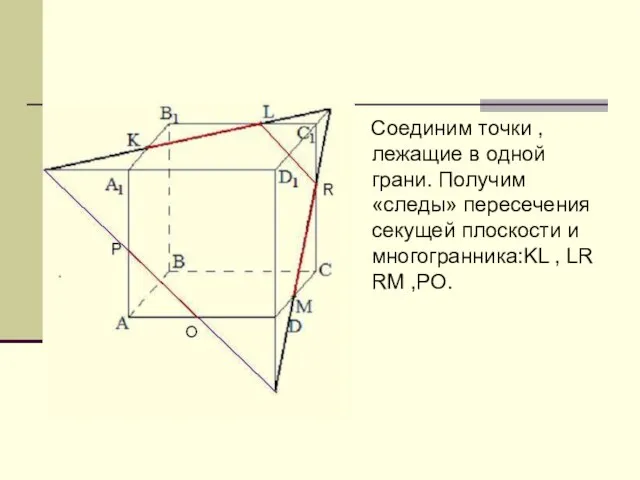
и многогранника:KL , LR RM ,PO.
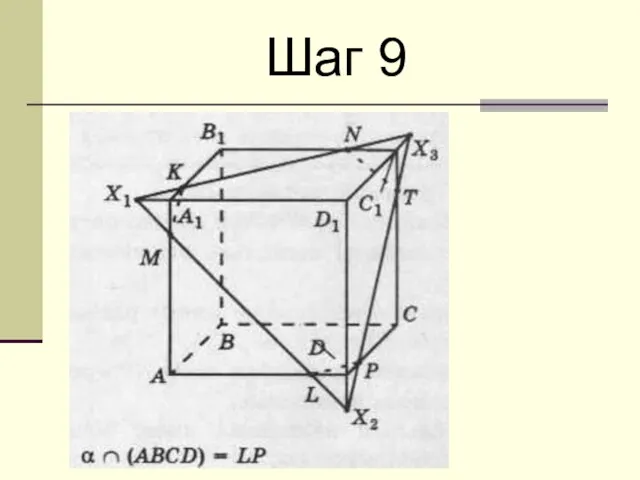
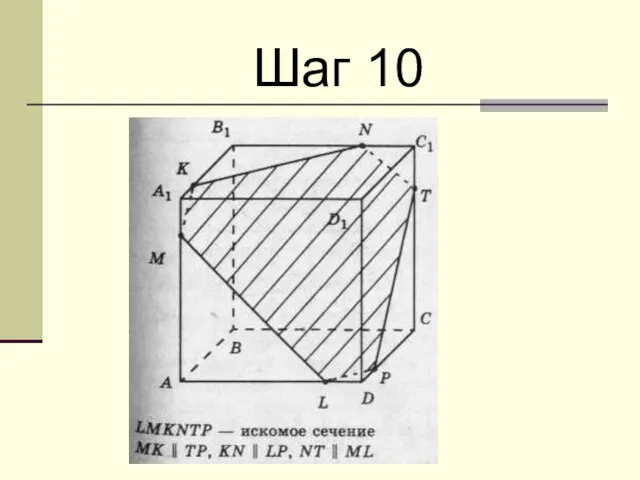
Слайд 9 Проводя аналогичным образом прямые в плоскостях других граней куба мы построим
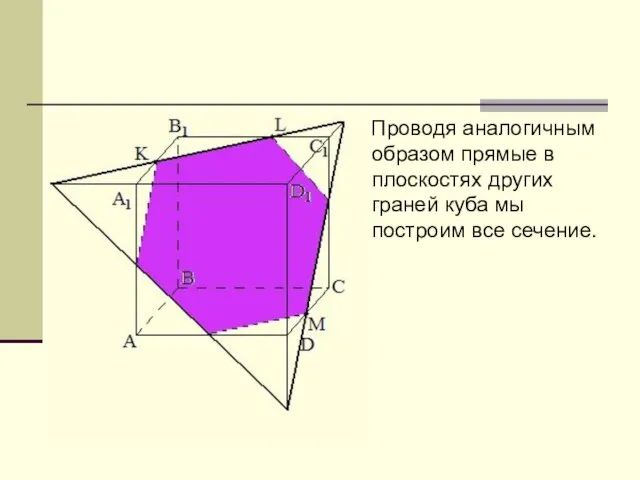
все сечение.
Слайд 10Сечение пирамиды плоскостью.
Задача 2: Постройте сечение пирамиды ABCD плоскостью проходящей через точки

K, L, M.
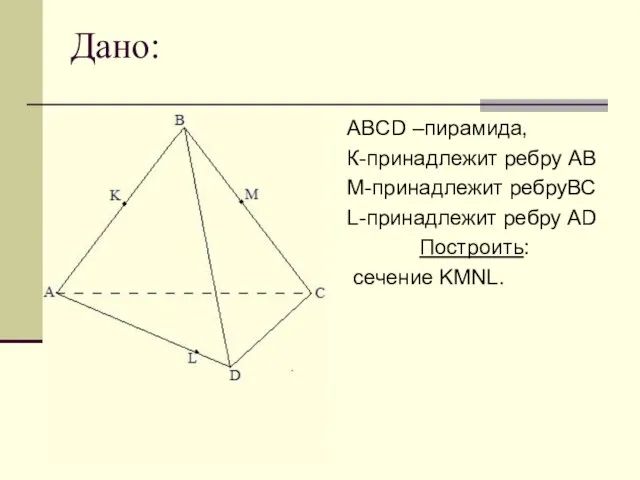
Слайд 11Дано:
ABCD –пирамида,
К-принадлежит ребру АВ
М-принадлежит ребруВС
L-принадлежит ребру AD
Построить:
сечение KMNL.
Слайд 12Решение:
Провести в плоскости ABD прямую KL (используя метод следов – прямые, по
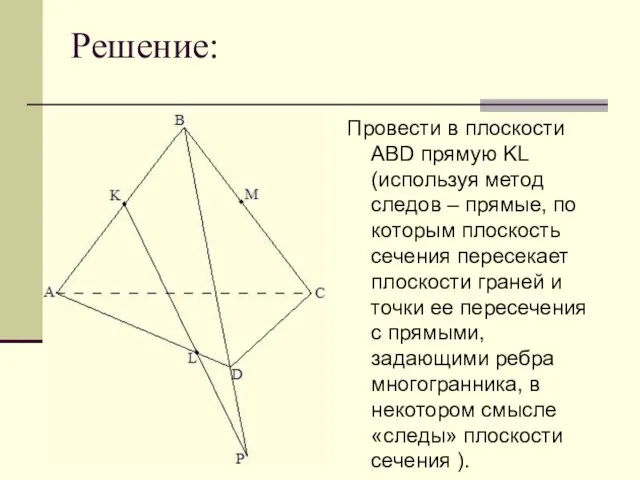
которым плоскость сечения пересекает плоскости граней и точки ее пересечения с прямыми, задающими ребра многогранника, в некотором смысле «следы» плоскости сечения ).
Слайд 13Обозначим через Р точку пересечения KL и BD.
Проводим прямую РМ, получаем точку
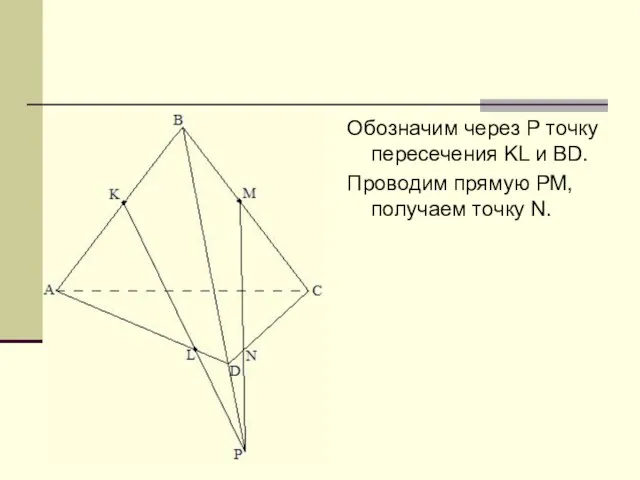
N.
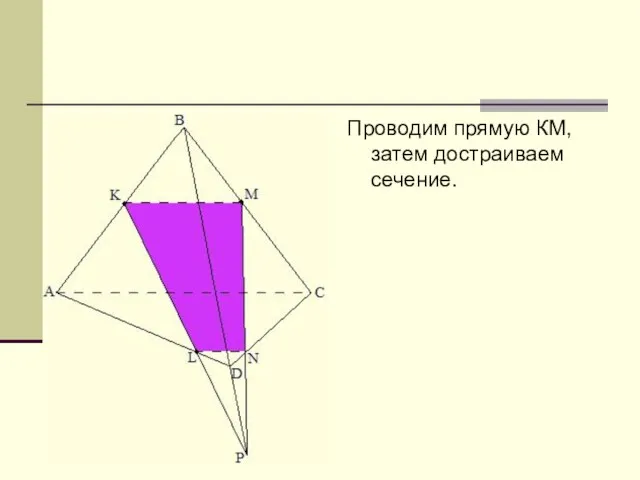
Слайд 14Проводим прямую КМ, затем достраиваем сечение.
Слайд 15задача
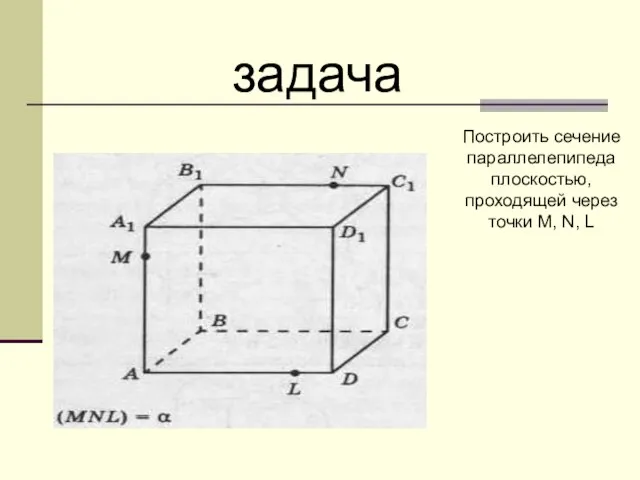
Построить сечение параллелепипеда плоскостью, проходящей через точки M, N, L
Слайд 26Построение сечении с использованием свойств параллельных плоскостей
Построить сечение плоскостью, проходящей через ребро
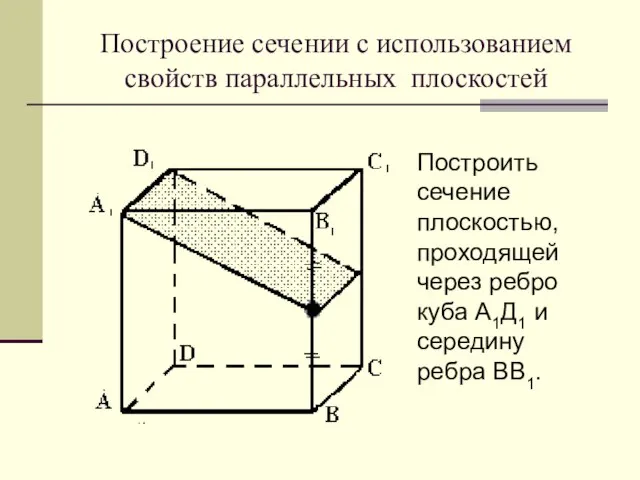
куба А1Д1 и середину ребра ВВ1.
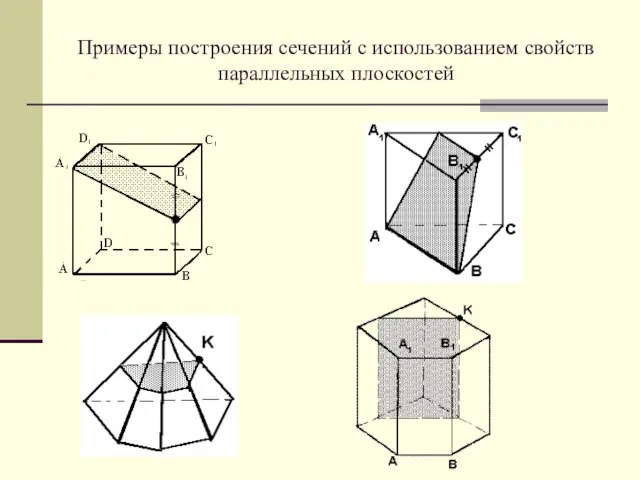
Слайд 27Примеры построения сечений с использованием свойств параллельных плоскостей
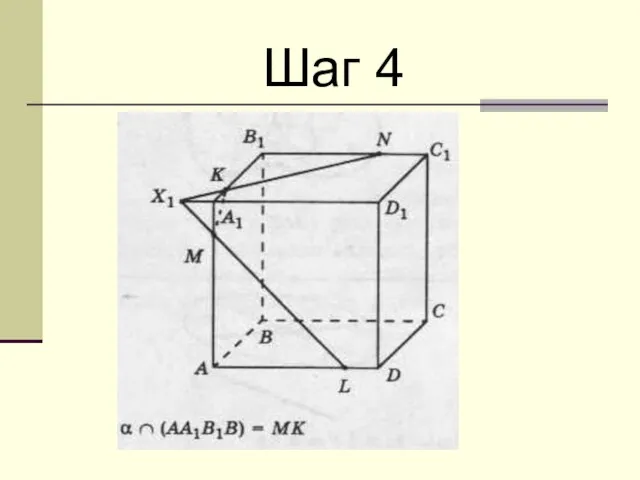
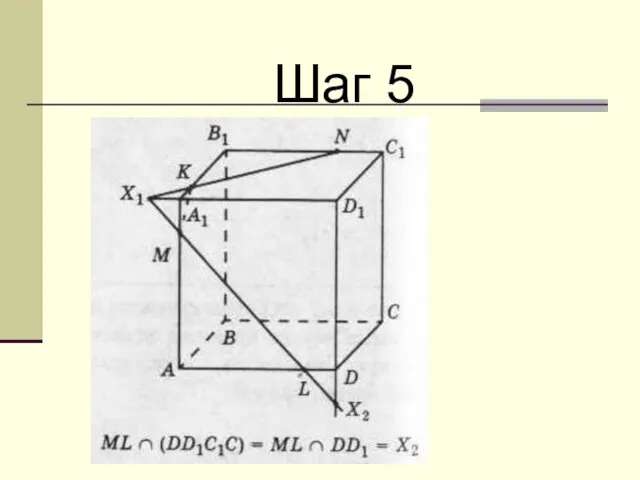
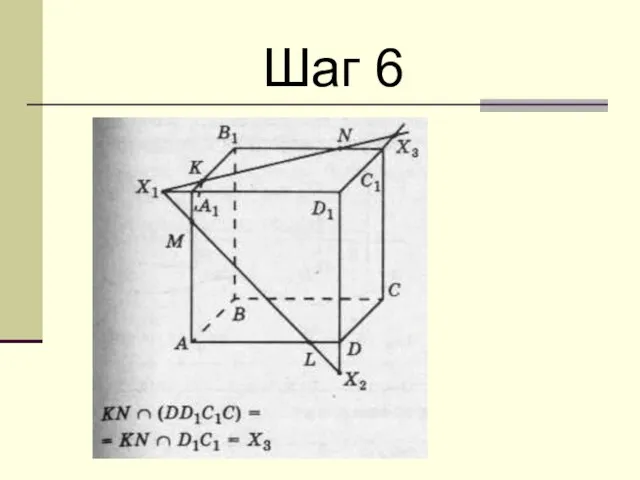
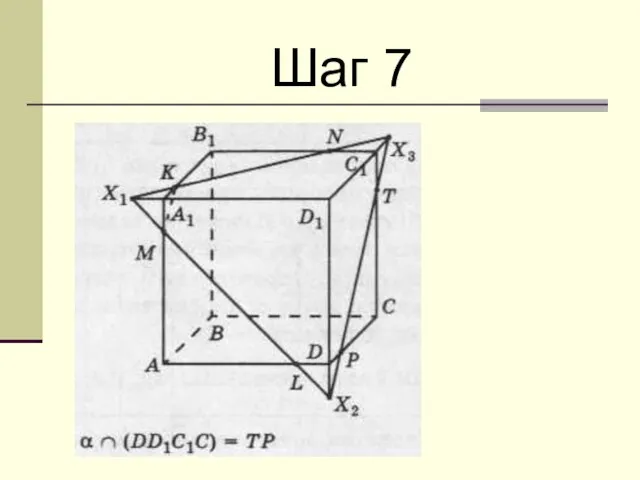
Слайд 28Задание 1:
На ребрах взяты точки K, L и M, как показано
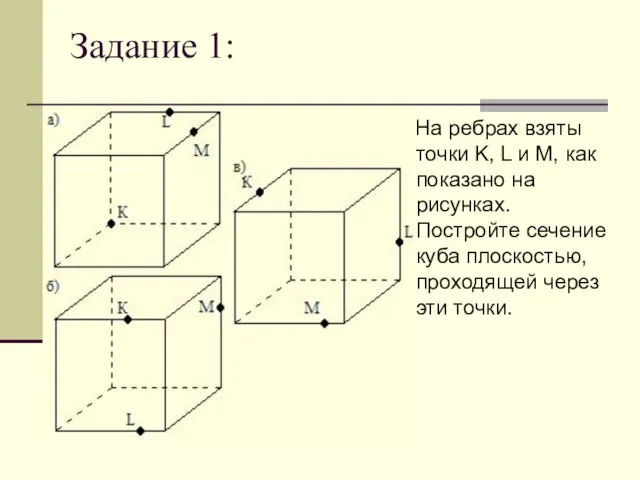
на рисунках. Постройте сечение куба плоскостью, проходящей через эти точки.

















 Презентация по математике "Решение задач на разностное и кратное сравнение чисел" -
Презентация по математике "Решение задач на разностное и кратное сравнение чисел" -  Игра - тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра - тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Презентация на тему Решение уравнений высших степеней
Презентация на тему Решение уравнений высших степеней  Метод подобия треугольников при решении задач
Метод подобия треугольников при решении задач Векторные задачи 1-го типа
Векторные задачи 1-го типа Matrix Algebra аnd Simultaneous Linear Equations. Lecture 10
Matrix Algebra аnd Simultaneous Linear Equations. Lecture 10 Действия с дробями
Действия с дробями Многогранники и круглые тела в мировой архитектуре
Многогранники и круглые тела в мировой архитектуре Презентация на тему Умножение числа 2
Презентация на тему Умножение числа 2  Обыкновенная дробь
Обыкновенная дробь Умножение обыкновенных дробей
Умножение обыкновенных дробей Декартова система координат
Декартова система координат Переместительное свойство сложения
Переместительное свойство сложения Формулы сокращенного умножения. Подготовка к СОР
Формулы сокращенного умножения. Подготовка к СОР Свойства натурального ряда чисел
Свойства натурального ряда чисел Обратные матрицы
Обратные матрицы Теорема о площади треугольников
Теорема о площади треугольников Презентация на тему Законы алгебры логики
Презентация на тему Законы алгебры логики  Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Пирамида. История
Пирамида. История Контрольная работа. Геометрия
Контрольная работа. Геометрия Параллельные плоскости
Параллельные плоскости Pakāpes vingrinājumi (bez atb)
Pakāpes vingrinājumi (bez atb) Координатная плоскость. Математика 6 класс
Координатная плоскость. Математика 6 класс Презентация на тему Прямоугольник
Презентация на тему Прямоугольник  Презентация на тему Треугольники (5 класс)
Презентация на тему Треугольники (5 класс)  algebr_drobi рабочая презентация начиная с 5 ссентября
algebr_drobi рабочая презентация начиная с 5 ссентября Аттестационная работа. Методическая разработка урока Единицы площади. Квадратный метр. 3 класс
Аттестационная работа. Методическая разработка урока Единицы площади. Квадратный метр. 3 класс