Содержание
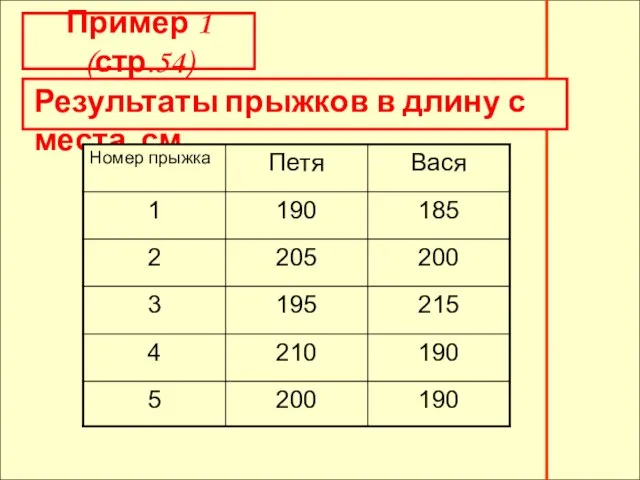
- 3. Наибольшее и наименьшее значение. Пример 1 Петя и Вася поспорили, кто лучше прыгает в длину с
- 4. Результаты прыжков в длину с места, см Пример 1 (стр.54)
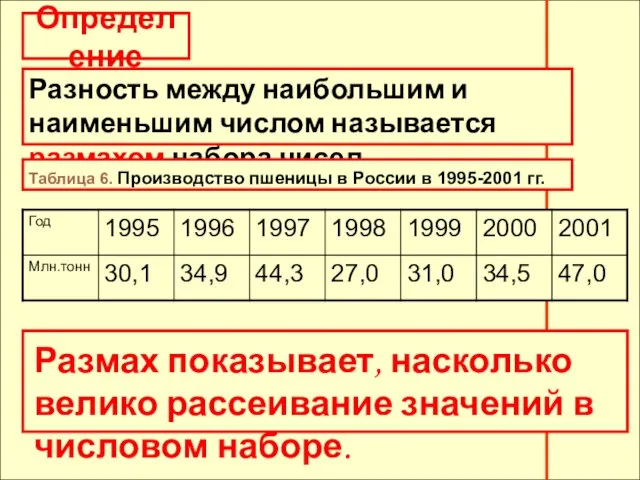
- 5. Определение Разность между наибольшим и наименьшим числом называется размахом набора чисел. Таблица 6. Производство пшеницы в
- 6. При изучении учебной нагрузки учащихся выделили группу из 12 семиклассников. Их попросили отметить в определенный день
- 7. При анализе сведений о времени, затраченном семиклассниками на выполнение домашнего задания по алгебре, нас могут интересовать
- 8. Рассмотрим еще пример. Пусть, проведя учет деталей, изготовленных за смену рабочими одной бригады, получили такой ряд
- 9. Например, в ряду чисел 47, 46, 50, 52, 47, 52, 49, 45, 43, 53 две моды
- 10. Итак, средняя выработка рабочих за смену составляет примерно 37 деталей; различие в выработке рабочих не превосходит
- 11. Упражнения №1. Найдите наибольшее и наименьшее значение, размах, среднее значение, медиану и моду набора чисел: а)
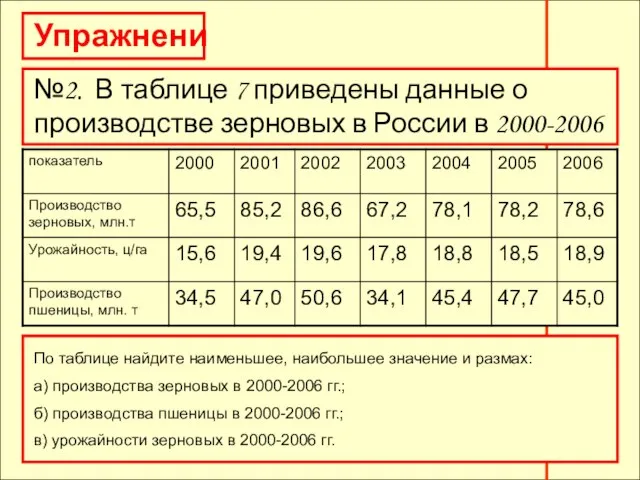
- 12. Упражнения №2. В таблице 7 приведены данные о производстве зерновых в России в 2000-2006 гг. По
- 13. Отклонения Попробуем узнать, как числа некоторого набора расположены по отношению к своему среднему значению. Зная только
- 14. Отклонения (продолжение) Получился новый набор -6, -1, 0, 2, 5 , который состоит из отклонений. Если
- 15. Отклонения (продолжение) Для любого набора, если только не все числа в нем равны, часть отклонений будет
- 16. Дисперсия Наиболее полной характеристикой разброса набора чисел является набор их отклонений от среднего арифметического. Но когда
- 17. Дисперсия Чтобы судить о разбросе, принято складывать не сами отклонения, а их квадраты. Квадраты отклонений неотрицательны,
- 18. Дисперсия Определение. Среднее арифметическое квадратов отклонений от среднего значения называется в статистике дисперсией набора чисел.
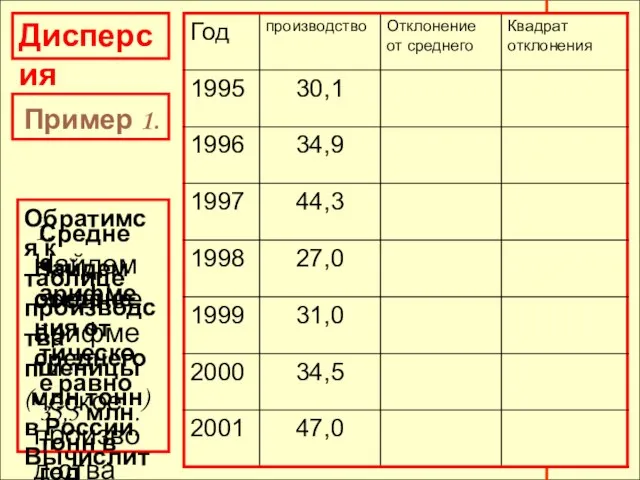
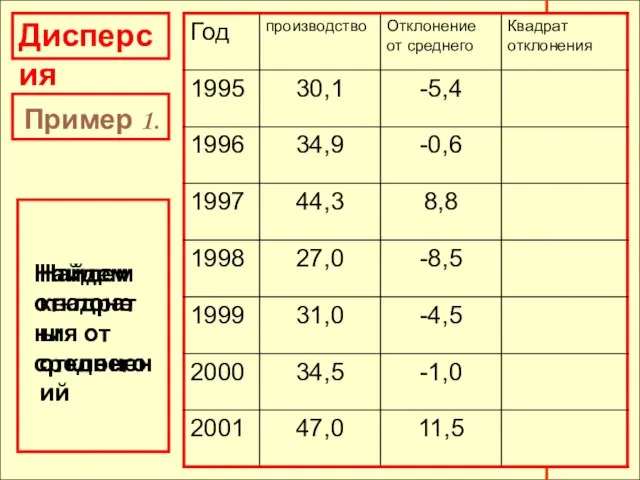
- 19. Дисперсия Пример 1. Обратимся к таблице производства пшеницы (млн.тонн) в России. Вычислить дисперсию. 1. Найдем среднее
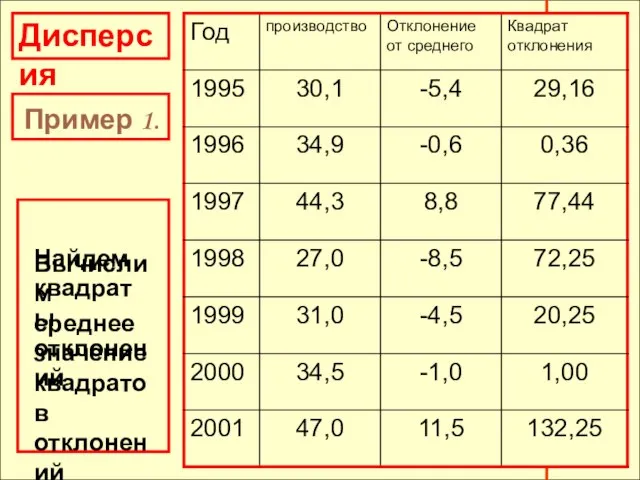
- 20. Дисперсия Пример 1. Найдем отклонения от среднего Найдем квадраты отклонений
- 21. Дисперсия Пример 1. Найдем квадраты отклонений Вычислим среднее значение квадратов отклонений
- 22. Дисперсия Пример 1. (29,16+0,36+77,44+72,25+20,25+1,00+132,25) :7=47,53. 47,53 - дисперсия
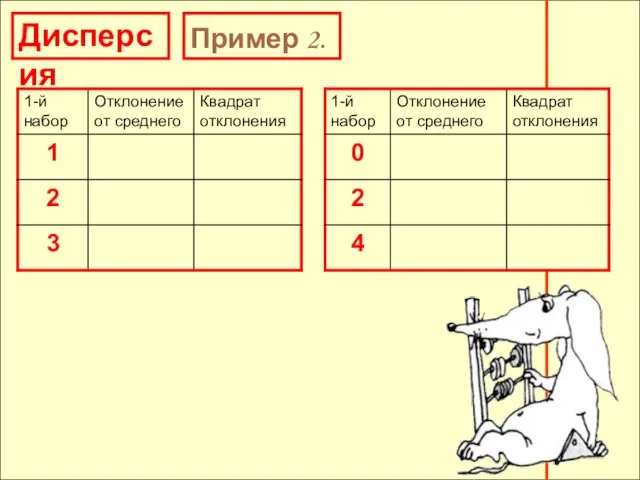
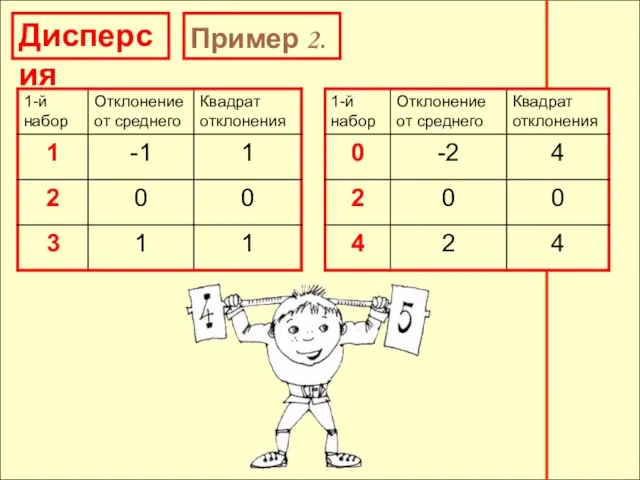
- 23. Дисперсия Пример 2. Покажем на простом примере, как дисперсия характеризует разброс отклонений. Возьмем два набора чисел
- 24. Дисперсия Пример 2.
- 25. Дисперсия Пример 2.
- 26. Дисперсия Пример 2.
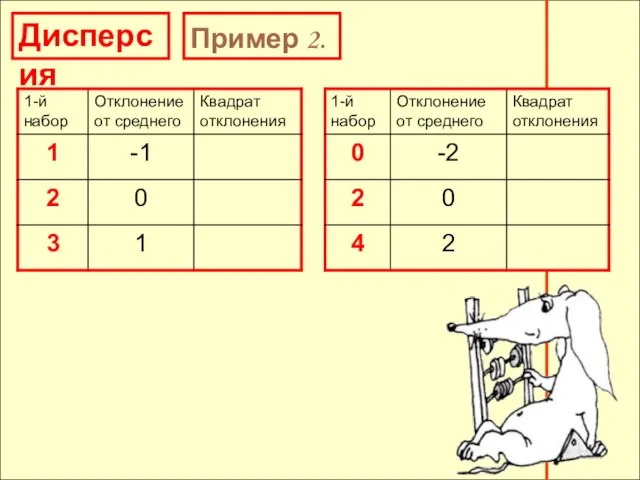
- 27. Дисперсия Пример 2. Дисперсия второго набора: (4 + 0 + 4): 3 = Дисперсия первого набора:
- 28. Дисперсия Пример 2. Дисперсия второго набора: (4 + 0 + 4): 3 = Дисперсия первого набора:
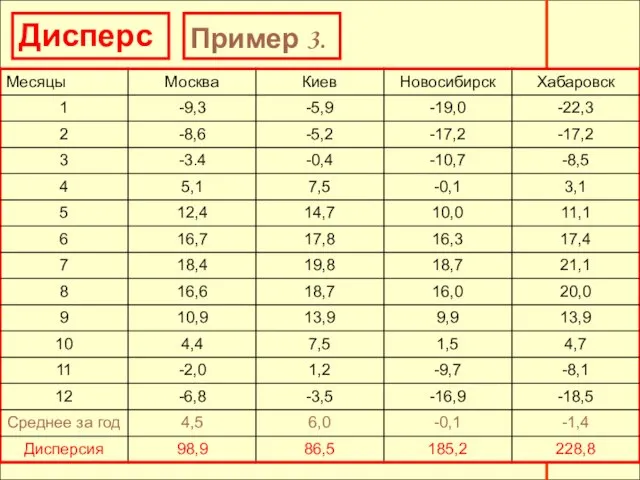
- 29. Дисперсия Пример 3. Континентальный климат отличается от умеренного более резкими изменениями температуры в течение года. В
- 30. Дисперсия Пример 3.
- 31. Упражнения №1 Для данных чисел вычислите среднее значение. Составьте таблицу отклонений от среднего и квадратов отклонений
- 32. Упражнения №2. Даны два набора чисел. Отметьте их на числовой прямой. Вычислите дисперсию каждого из этих
- 33. Упражнения №3. Даны два набора чисел. Отметьте их на числовой прямой. Вычислите дисперсию каждого из этих
- 34. Обозначения и формулы Числа в наборах часто приходиться обозначать буквами, подобно тому, как это делается при
- 35. Обозначения и формулы Среднее арифметическое чисел х1, х2, х3, х4, х5 принято обозначать через Например, среднее
- 36. Обозначения и формулы Отклонения от среднего значения теперь запишутся так: Разберем на примере набора х1, х2,
- 37. Обозначения и формулы №1. Запишите с помощью букв набор чисел 17, 3, 6, 21, 15. Чему
- 38. Свойства среднего арифметического и дисперсии Буквенные обозначения чисел в наборе и введенные обозначения для среднего арифметического
- 39. Свойства среднего арифметического и дисперсии Рассмотрим набор чисел х1, х2, х3, х4, х5. Пусть - его
- 40. Свойство 1. Среднее арифметическое набора х1+а, х2+а, х3+а, х4+а, х5+а равно
- 41. Свойство 2. Дисперсия набора х1+а, х2+а, х3+а, х4+а, х5+а равна дисперсии набора х1, х2, х3, х4,
- 43. Скачать презентацию






























 Презентация на тему Кто хочет стать отличником
Презентация на тему Кто хочет стать отличником  Согласование существительных с числительными
Согласование существительных с числительными Сложение и вычитание десятичных дробей. Электронный урок
Сложение и вычитание десятичных дробей. Электронный урок Умножение десятичных дробей тренажёр 5 класс
Умножение десятичных дробей тренажёр 5 класс Час занимательной математики. 5 класс
Час занимательной математики. 5 класс Презентация на тему ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
Презентация на тему ЦЕНТРАЛЬНАЯ СИММЕТРИЯ  Сопоставимость показателей. Лекция 2
Сопоставимость показателей. Лекция 2 Куб. Формулы для куба
Куб. Формулы для куба Графики элементарных функций. Повторение
Графики элементарных функций. Повторение Равносильность уравнений. 11 класс
Равносильность уравнений. 11 класс Возведение одночлена в степень
Возведение одночлена в степень Объем наклонной призмы
Объем наклонной призмы Параллелепипед. 10 класс
Параллелепипед. 10 класс Взаимное расположение двух окружностей
Взаимное расположение двух окружностей Умножение натуральных чисел. Графический диктант. 5 класс
Умножение натуральных чисел. Графический диктант. 5 класс Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Умножение десятичных дробей
Умножение десятичных дробей Л 7 Предел числовой последовательности
Л 7 Предел числовой последовательности Параллельные прямые
Параллельные прямые Что в центре круга (1 класс)
Что в центре круга (1 класс) Гомотетия. Гомотетичные фигуры
Гомотетия. Гомотетичные фигуры Математика вокруг нас
Математика вокруг нас 1 замечательный предел
1 замечательный предел Фракталы в литературе
Фракталы в литературе Тригонометрические уравнения. Однородные тригонометрические уравнения
Тригонометрические уравнения. Однородные тригонометрические уравнения Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Решение простейших логарифмических уравнений
Решение простейших логарифмических уравнений Названия чисел в записях действий
Названия чисел в записях действий