Содержание
- 2. На уроках алгебры мы разбивали сумму на два слагаемых: Это довольно трудоёмкий процесс, поэтому появилась идея
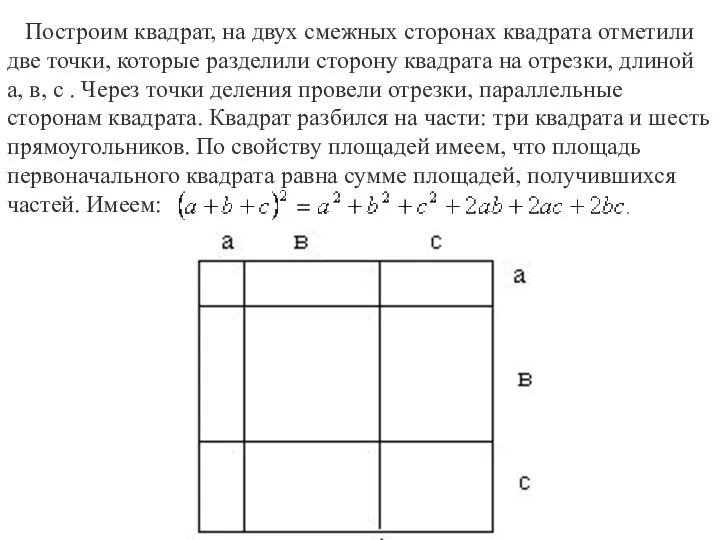
- 3. Построим квадрат, на двух смежных сторонах квадрата отметили две точки, которые разделили сторону квадрата на отрезки,
- 4. Аналогично, построим квадрат, на смежных сторонах квадрата отметим три точки, которые разделят стороны квадрата на отрезки
- 6. Скачать презентацию


 Применение теоремы Пифагора
Применение теоремы Пифагора Свойства случайных погрешностей
Свойства случайных погрешностей Презентация на тему Занимательная геометрия (3 класс)
Презентация на тему Занимательная геометрия (3 класс)  Подготовка к контрольной работе
Подготовка к контрольной работе Путешествие на воздушных шарах
Путешествие на воздушных шарах Внеурочная деятельность по математике, 3 класс
Внеурочная деятельность по математике, 3 класс Сумма углов треугольника
Сумма углов треугольника деление многочлена на многочлен столбиком
деление многочлена на многочлен столбиком Канонический вид многочлена с одной переменной (урок 65)
Канонический вид многочлена с одной переменной (урок 65) Множества. Решение задач
Множества. Решение задач Уменьшаемое, вычитаемое, разность
Уменьшаемое, вычитаемое, разность Пересекающиеся и параллельные прямые
Пересекающиеся и параллельные прямые Площадь криволинейной трапеции
Площадь криволинейной трапеции Компетентностно-ориентированные задания, как средство формирования ключевых компетенций учащихся
Компетентностно-ориентированные задания, как средство формирования ключевых компетенций учащихся Презентация на тему Отношения и пропорции
Презентация на тему Отношения и пропорции  Презентация на тему Иррациональные числа (8 класс)
Презентация на тему Иррациональные числа (8 класс)  Функции и их графики. 9 класс
Функции и их графики. 9 класс Страничка для любознательных
Страничка для любознательных Решение тригонометрических уравнений
Решение тригонометрических уравнений Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Нахождение произведения по предыдущему результату. Замена умножения сложением
Нахождение произведения по предыдущему результату. Замена умножения сложением Решение планиметрических задач
Решение планиметрических задач Логарифмы
Логарифмы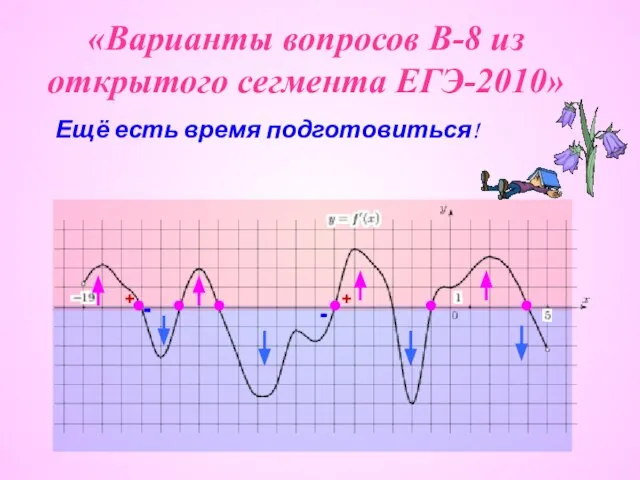 Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Задачи на проценты
Задачи на проценты Геометрия пчелиных сот
Геометрия пчелиных сот Тригонометрические функции двойного угла
Тригонометрические функции двойного угла Количественные характеристики встречаемости заболеваний
Количественные характеристики встречаемости заболеваний