Экстремумы (1)

2.Исследование функции на экстремум с помощью первой производной

2.Определение
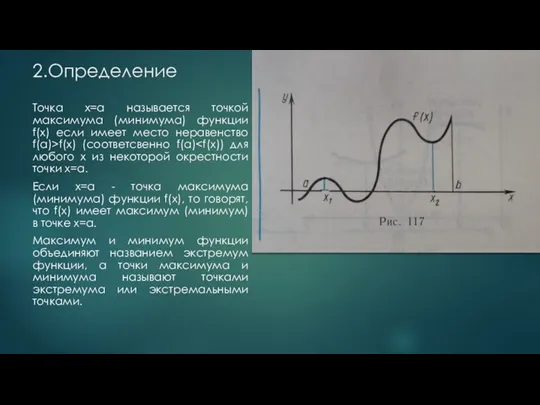
Точка х=a называется точкой максимума (минимума) функции f(x) если имеет место неравенство f(a)>f(x) (соответсвенно f(a)
Если x=a - точка максимума (минимума) функции f(x), то говорят, что f(x) имеет максимум (минимум) в точке x=a.
Максимум и минимум функции объединяют названием экстремум функции, а точки максимума и минимума называют точками экстремума или экстремальными точками.

Теорема 3.
Если x=a является точкой экстремума функ- Рис.118 Рис.119
ции y=f(x) и производная в этой точке существует, то она равна нулю: f`(a)=0
геометрически необходимый признак экстремума означает,что если x=a-точка
экстремума функции y=f(x),то касательная (в том случае,когда она существует)
к графику этой функции в точке (a; f(a)) параллельна оси Ox ( рис.118).
Обращение первой производной в нуль является необходимым, но не достаточным условием экстремума.
Теорема 4.( достаточный признак экстремума).Если производная f`(x) при переходе
X через a меняет знак, то а является точкой экстремума функции f(x).