повторение 8 класса

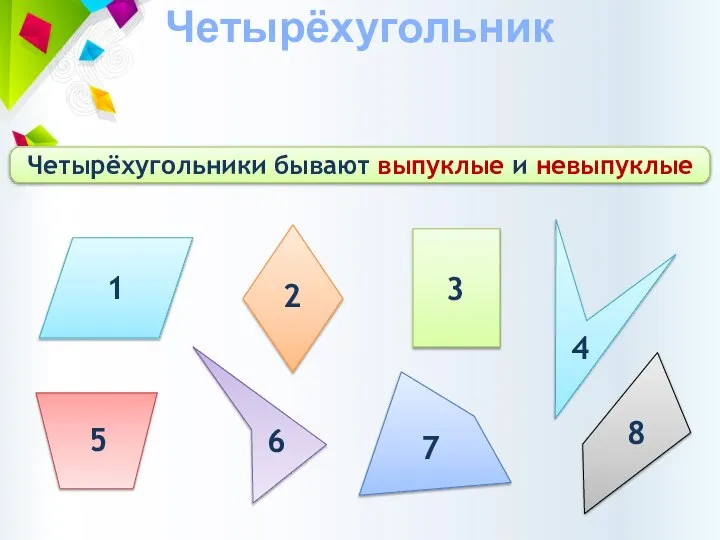
Четырёхугольник
Четырёхугольники бывают выпуклые и невыпуклые

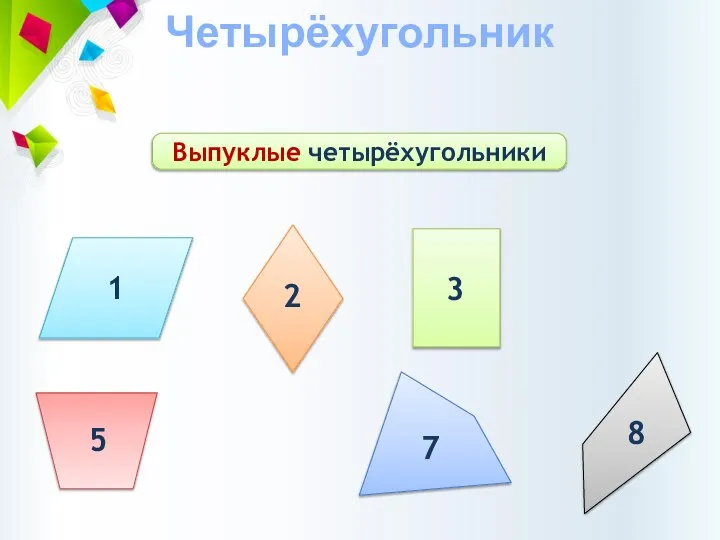
Четырёхугольник
Выпуклые четырёхугольники

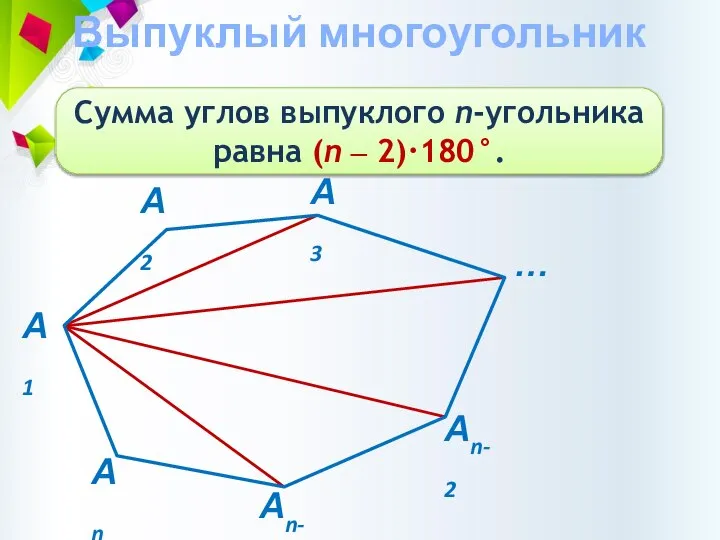
Выпуклый многоугольник
Сумма углов выпуклого n-угольника равна (n ‒ 2)·180°.

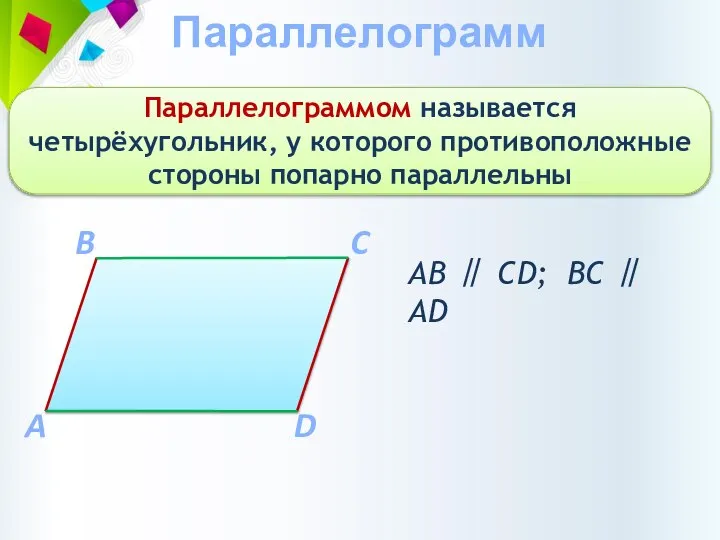
Параллелограмм
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны
A
C
B
D
АВ ∥ CD; BC ∥ AD

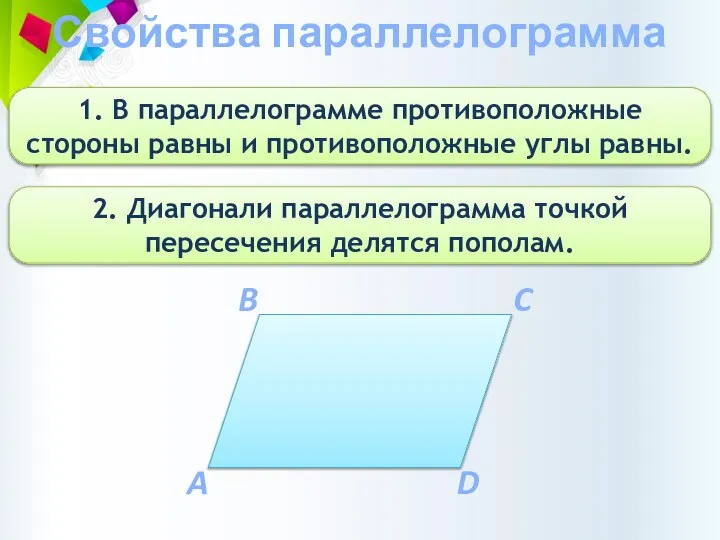
Свойства параллелограмма
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
A
C
B
D

Признаки параллелограмма
1) Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник ‒ параллелограмм.
2) Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник ‒ параллелограмм.
3) Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник ‒ параллелограмм.

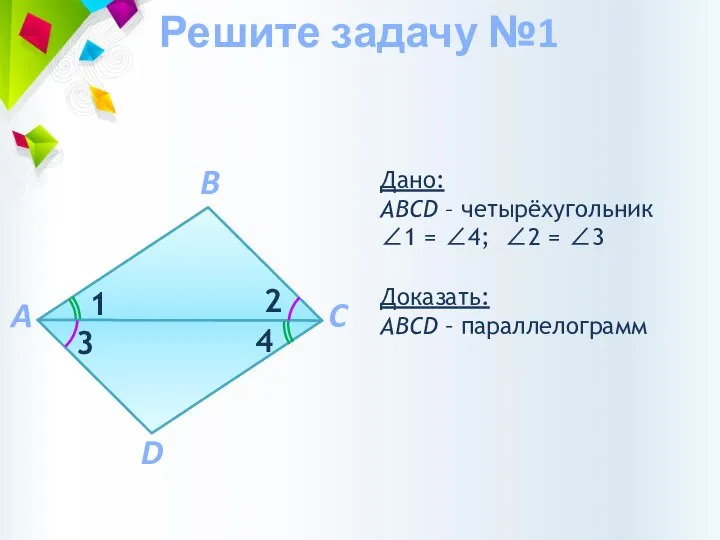
Доказать:
АВCD – параллелограмм
Дано:
АВCD – четырёхугольник
∠1 = ∠4; ∠2 = ∠3
Решите задачу №1

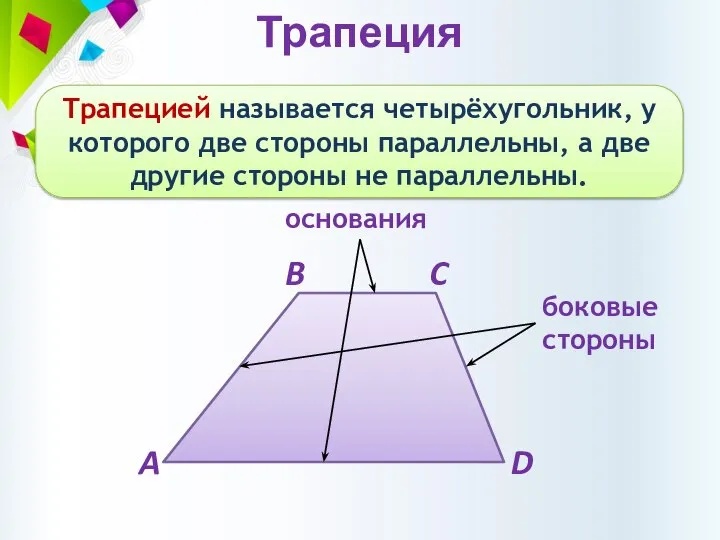
Трапеция
Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
основания
боковые стороны

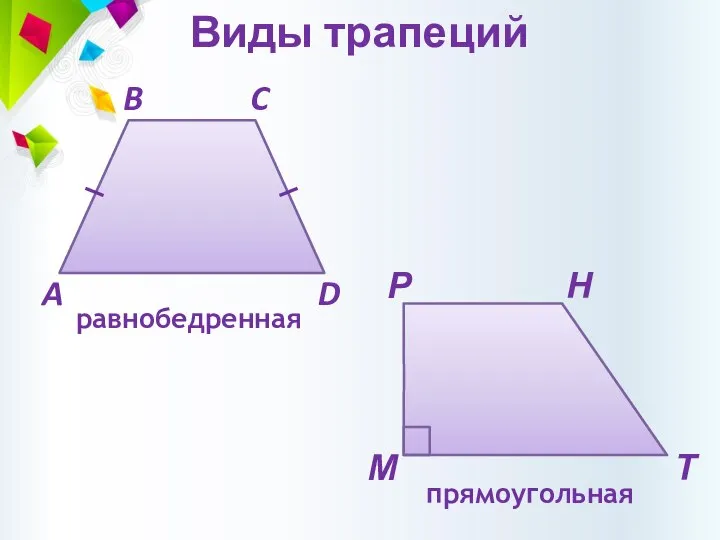
Виды трапеций
прямоугольная
равнобедренная

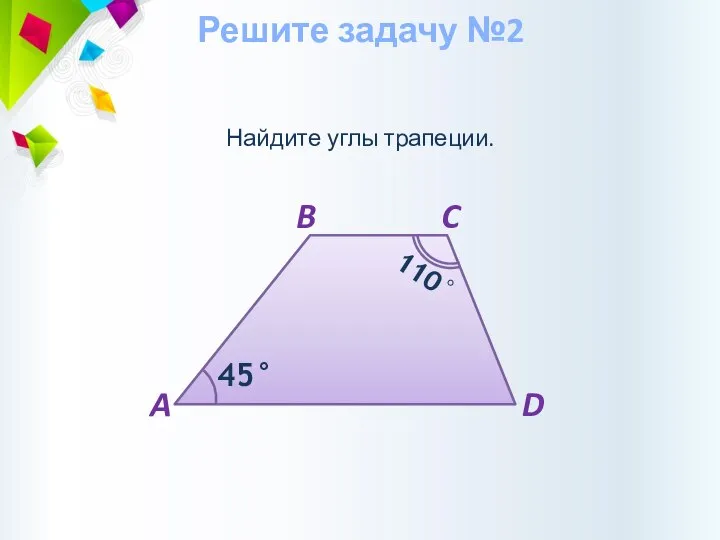
Найдите углы трапеции.
Решите задачу №2

Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые
A
C
B
D
∠А=∠В=∠С=∠D=90°
АВ ∥ CD; BC ∥ AD
АВ = CD; BC = AD
АО = ОC; BО = ОD
О

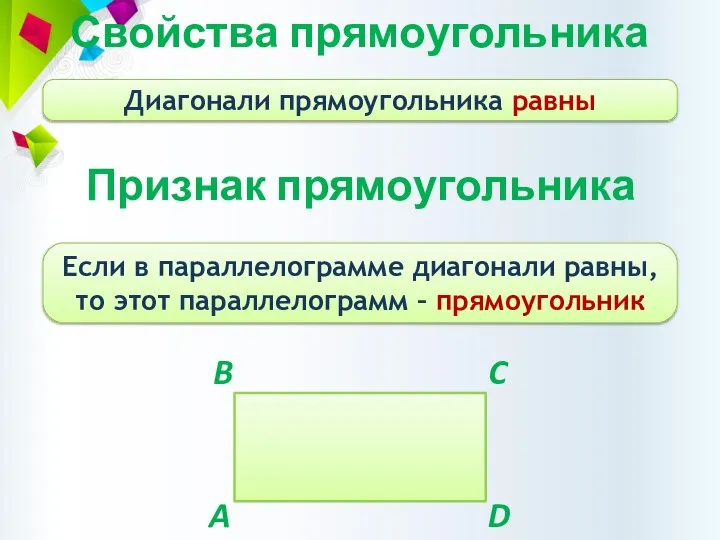
Свойства прямоугольника
Диагонали прямоугольника равны
Признак прямоугольника
Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник

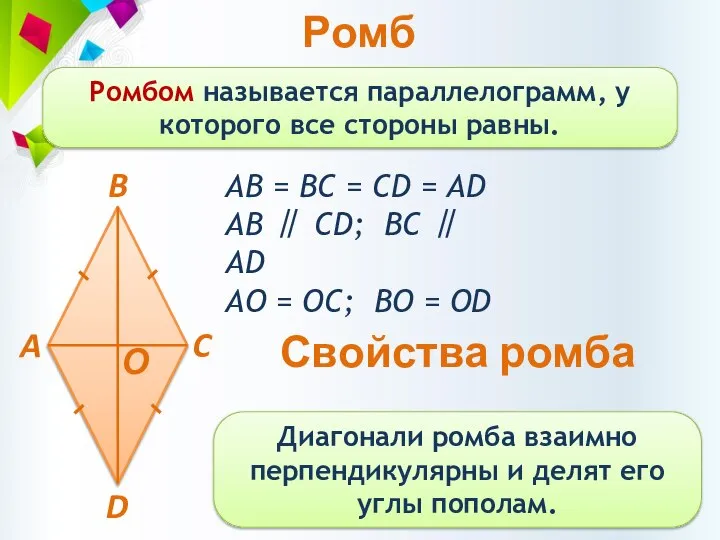
Ромб
Ромбом называется параллелограмм, у которого все стороны равны.
АВ = BC = CD = AD
АВ ∥ CD; BC ∥ AD
АО = ОC; BО = ОD
Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Свойства ромба

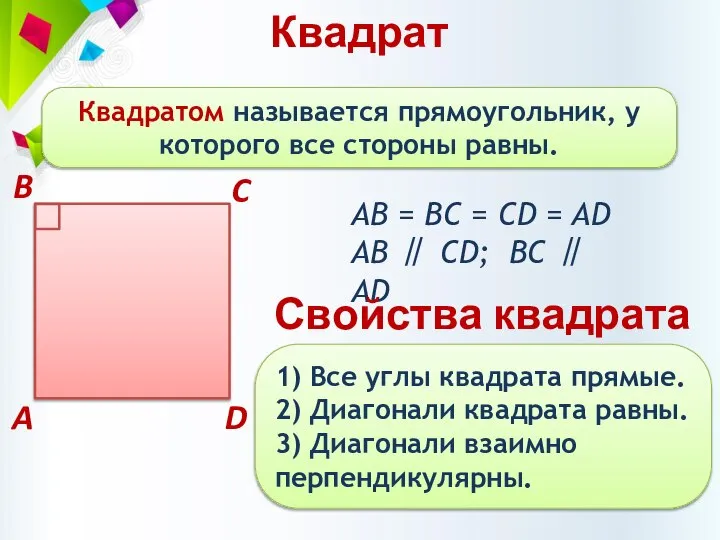
Квадрат
Квадратом называется прямоугольник, у которого все стороны равны.
АВ = BC = CD = AD
АВ ∥ CD; BC ∥ AD
Свойства квадрата
1) Все углы квадрата прямые.
2) Диагонали квадрата равны.
3) Диагонали взаимно перпендикулярны.

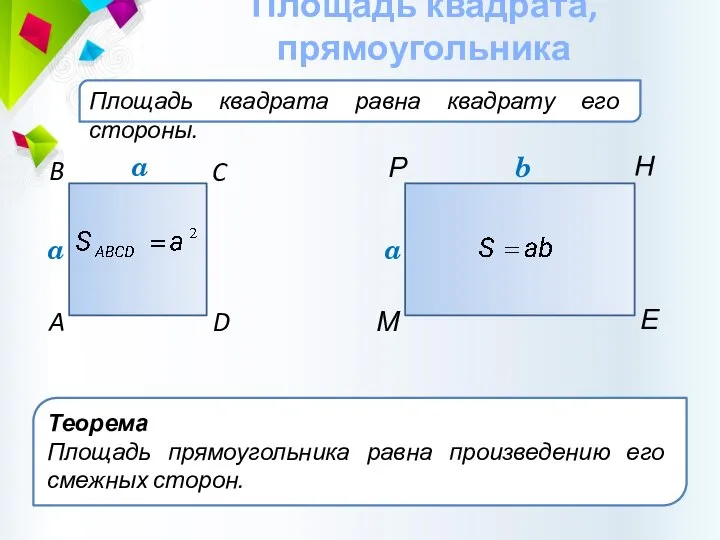
Площадь квадрата равна квадрату его стороны.
Площадь квадрата, прямоугольника
C
B
D
A
a
Теорема
Площадь прямоугольника равна произведению его смежных сторон.
Н
Р
Е
М
a
b
a

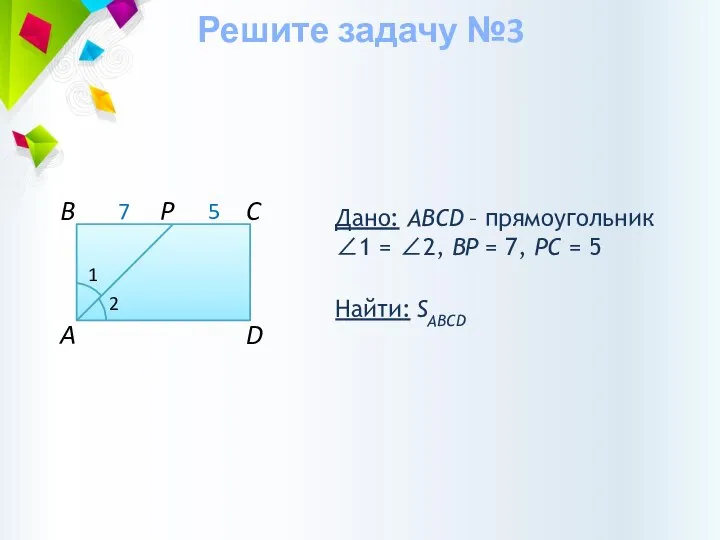
Дано: ABCD – прямоугольник
∠1 = ∠2, BP = 7, РC = 5
Найти: SABCD
P
1
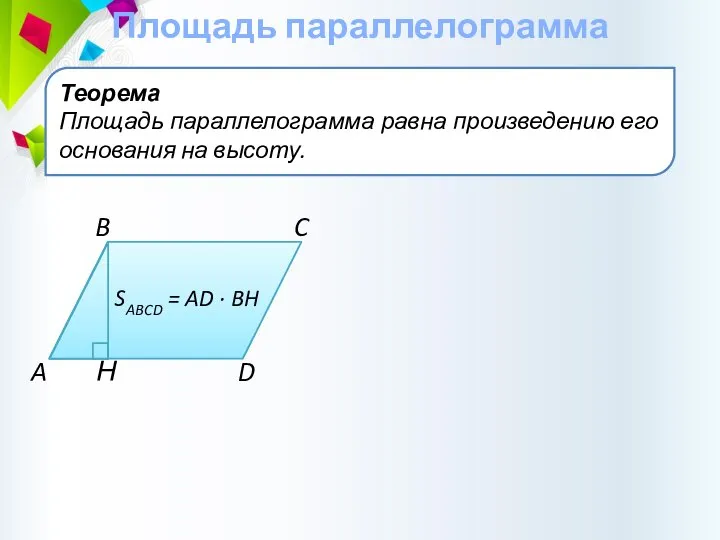
Решите задачу №3

Теорема
Площадь параллелограмма равна произведению его основания на высоту.
Площадь параллелограмма
C
B
D
A
Н
SABCD = AD · BH

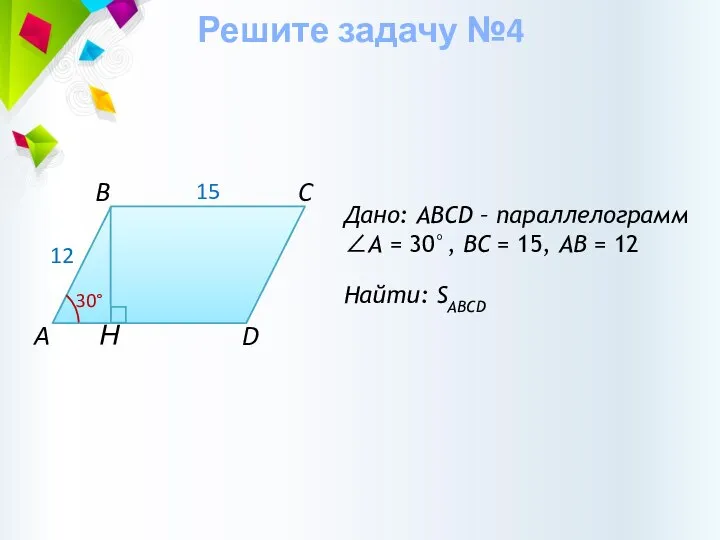
Н
Дано: ABCD – параллелограмм
∠А = 30°, BС = 15, АВ = 12
Найти: SABCD
Решите задачу №4

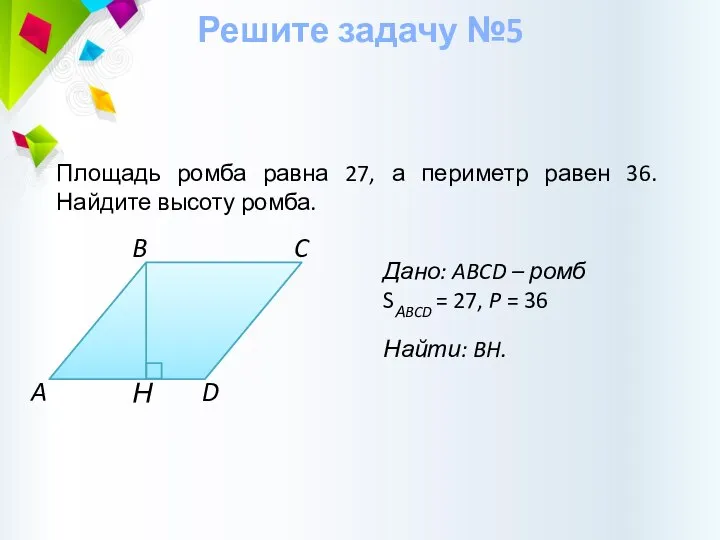
Н
Дано: ABCD – ромб
SАBCD = 27, P = 36
Найти: BH.
Решите задачу №5
Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.

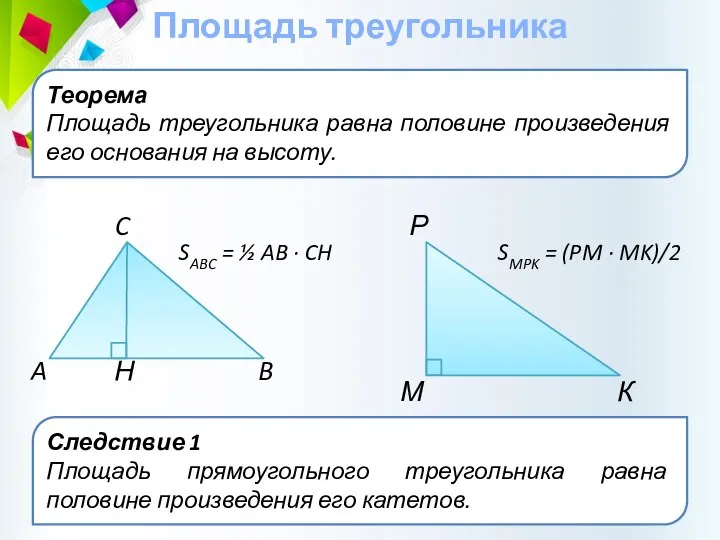
Теорема
Площадь треугольника равна половине произведения его основания на высоту.
Площадь треугольника
C
B
A
Н
Следствие 1
Площадь прямоугольного треугольника равна половине произведения его катетов.
М
К
Р
SABC = ½ AB · CH
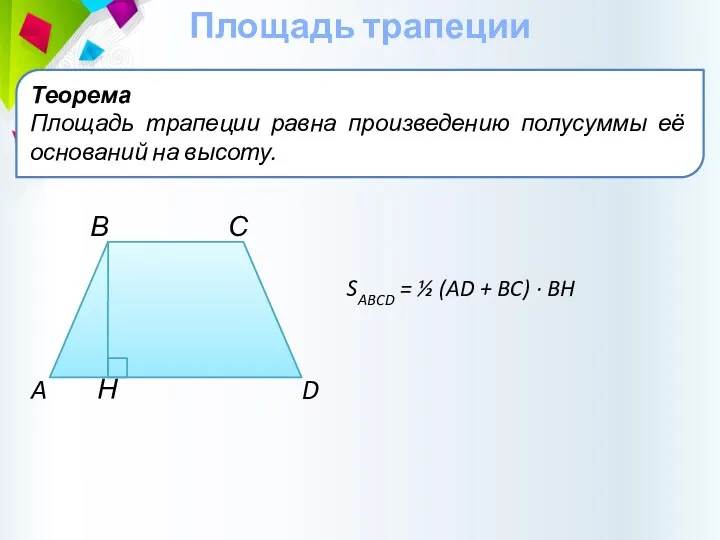
SMPK = (PM · MK)/2

Площадь трапеции
Теорема
Площадь трапеции равна произведению полусуммы её оснований на высоту.
В
С
A
Н
D
SABCD = ½ (AD + BC) · BH

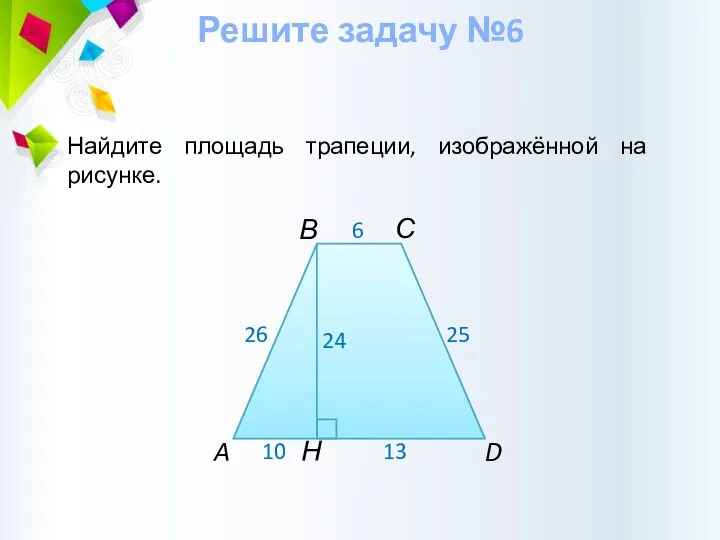
Решите задачу №6
Найдите площадь трапеции, изображённой на рисунке.

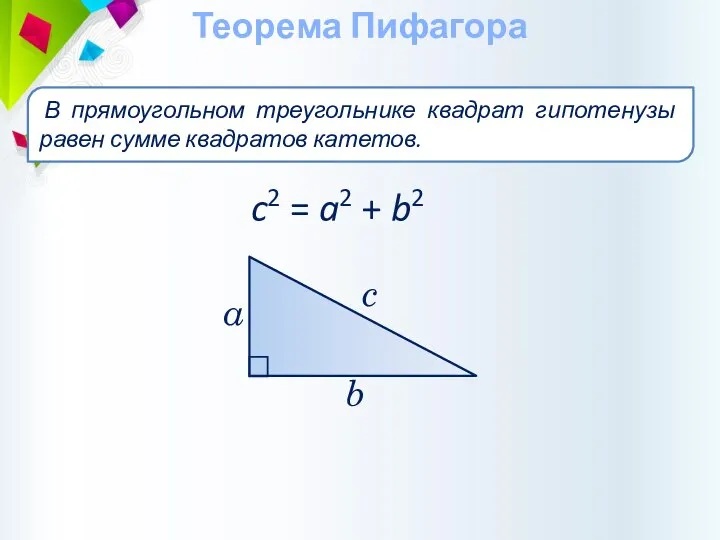
Теорема Пифагора
c2 = a2 + b2
c
b
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
a

Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

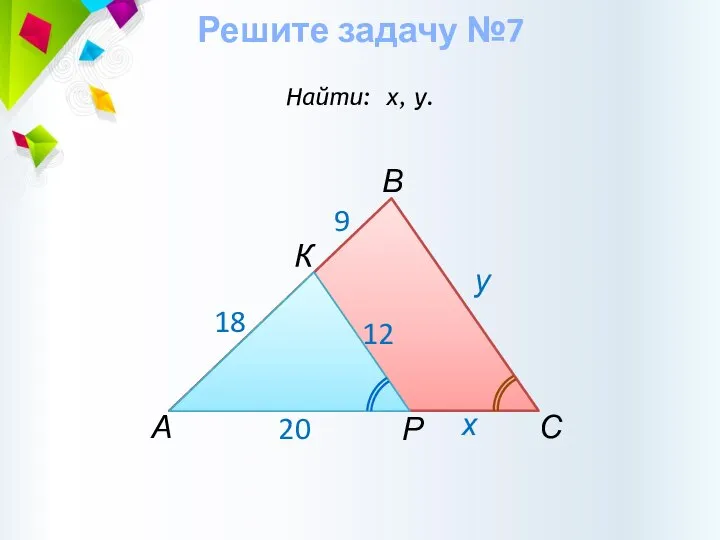
Решите задачу №7
Найти: х, у.
А
В
С
у
х
Р
К
18
20
9
12

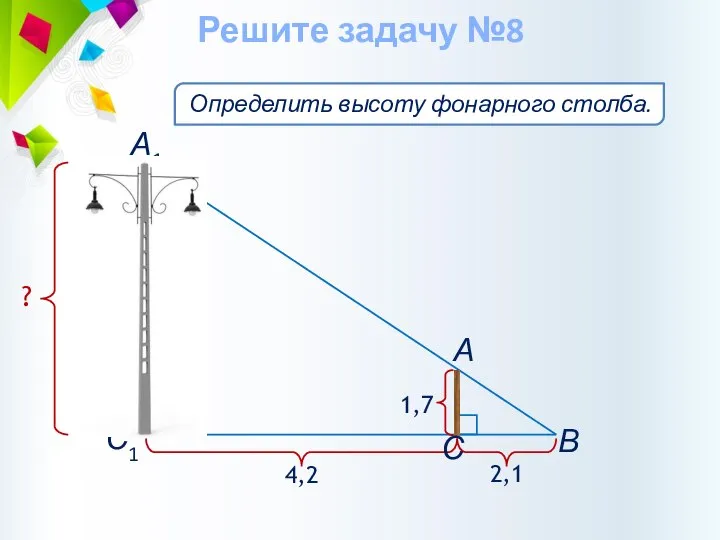
Определить высоту фонарного столба.
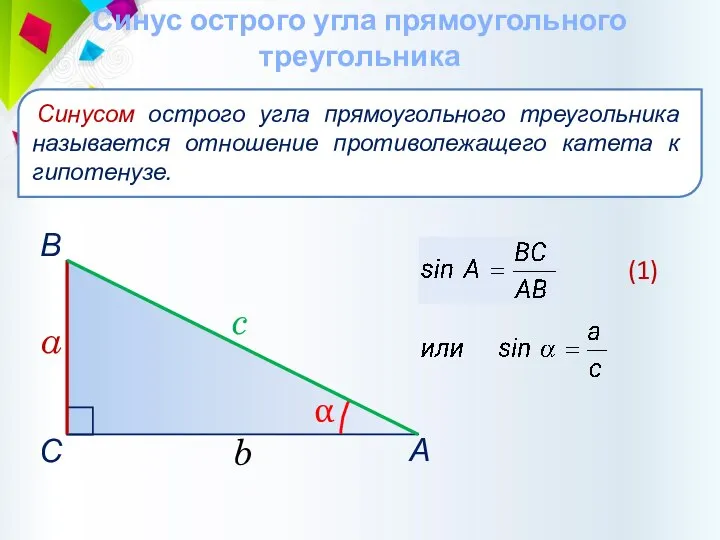
Решите задачу №8

Синус острого угла прямоугольного треугольника
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
c
b
a
α
А
В
С
(1)

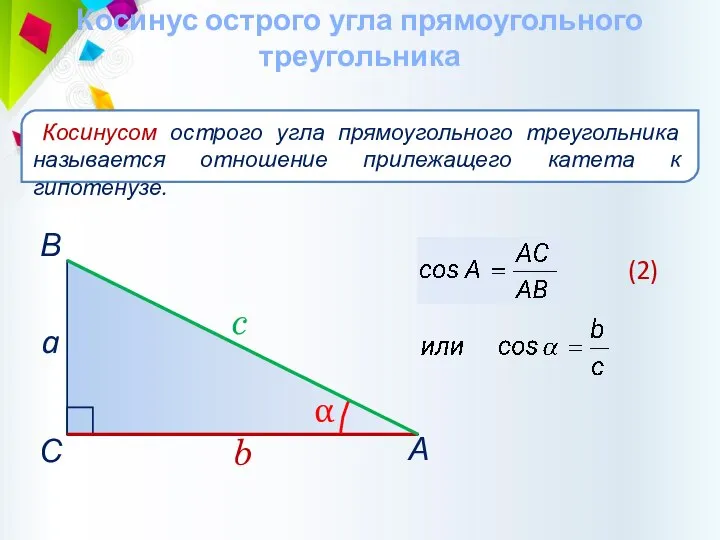
Косинус острого угла прямоугольного треугольника
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
c
b
a
α
А
В
С
(2)

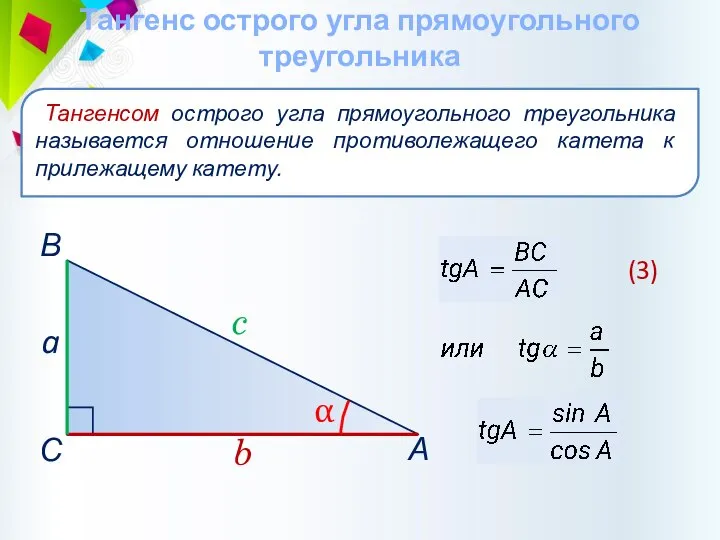
Тангенс острого угла прямоугольного треугольника
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
c
b
a
α
А
В
С
(3)

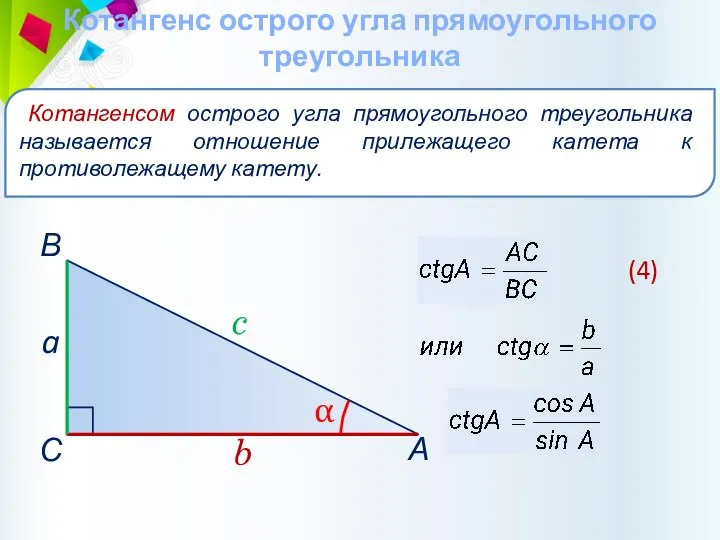
Котангенс острого угла прямоугольного треугольника
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету.
c
b
a
α
А
В
С
(4)

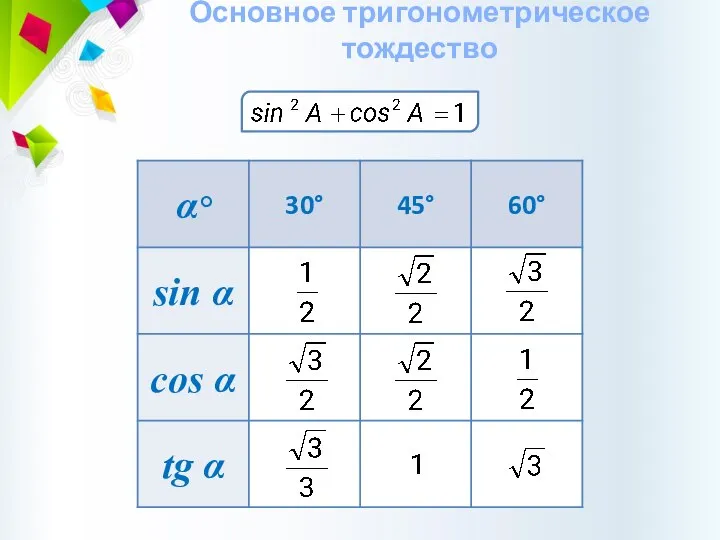
Основное тригонометрическое тождество

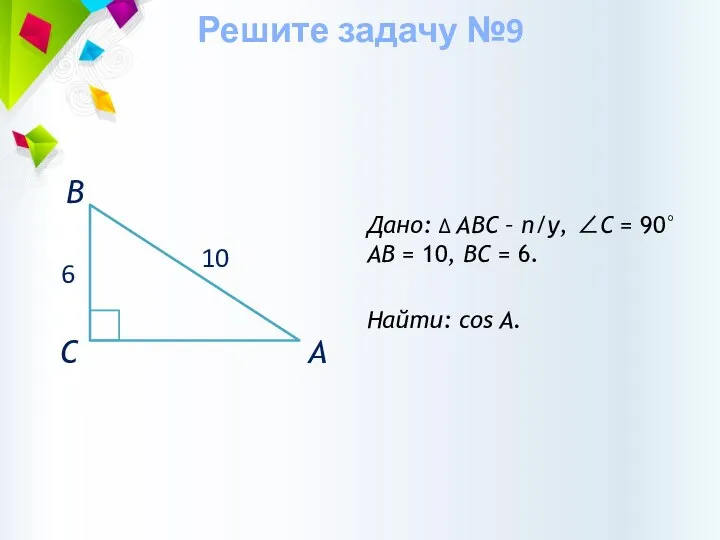
Дано: ∆ АВС – п/у, ∠С = 90°
АВ = 10, ВС = 6.
Найти: cos A.
Решите задачу №9

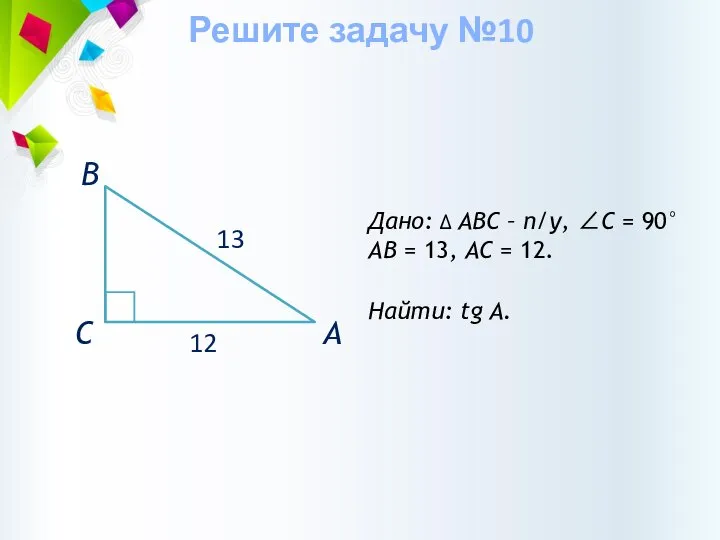
Дано: ∆ АВС – п/у, ∠С = 90°
АВ = 13, АС = 12.
Найти: tg A.
Решите задачу №10

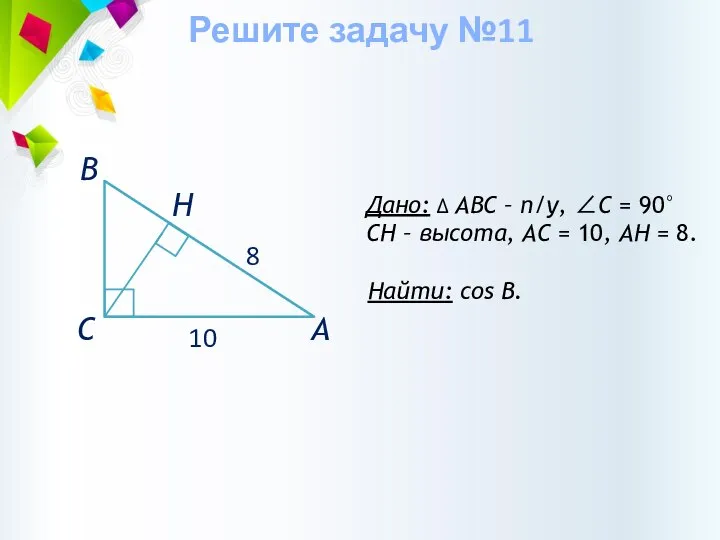
Дано: ∆ АВС – п/у, ∠С = 90°
CH – высота, АС = 10, АН = 8.
Найти: cos B.
Решите задачу №11

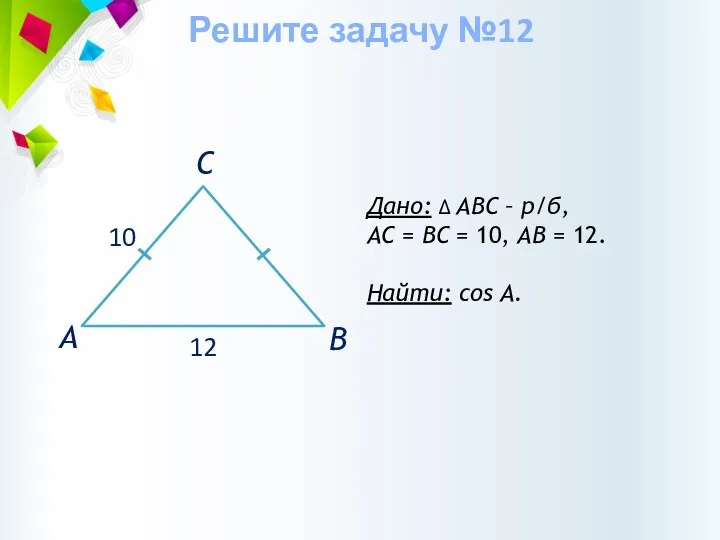
Дано: ∆ АВС – р/б,
АС = ВС = 10, АВ = 12.
Найти: cos А.
Решите задачу №12

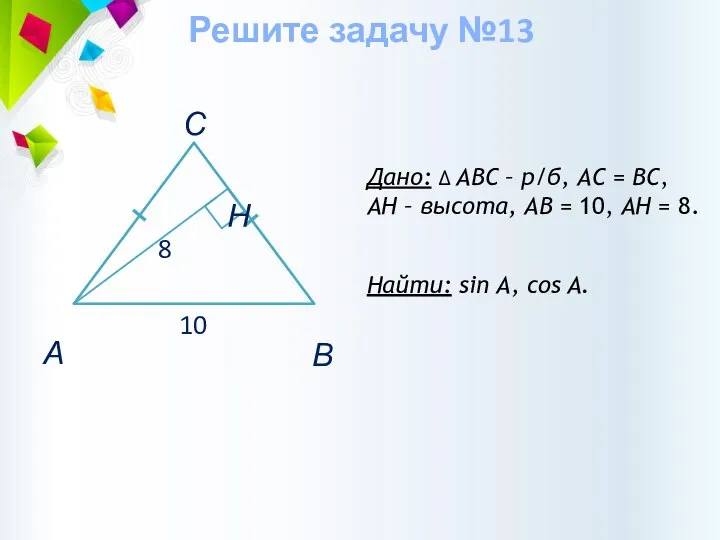
Дано: ∆ АВС – р/б, АС = ВС,
AH – высота, АВ = 10, AH = 8.
Найти: sin А, cos A.
Решите задачу №13

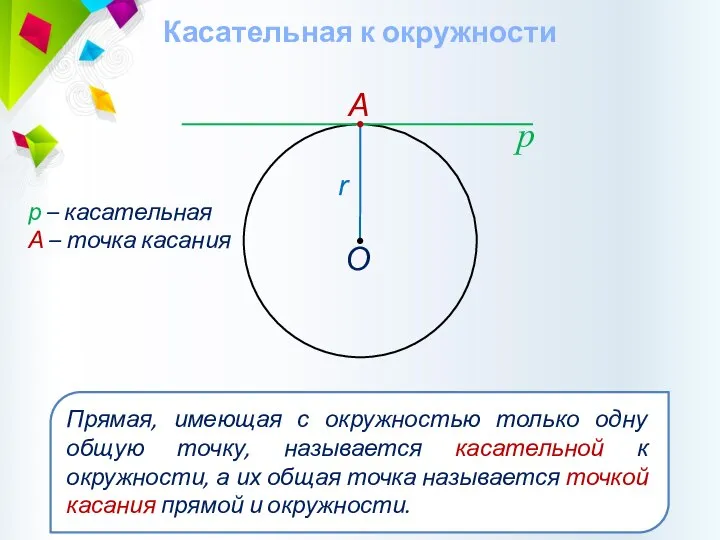
Касательная к окружности
р
р – касательная
А – точка касания
А
О
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
r

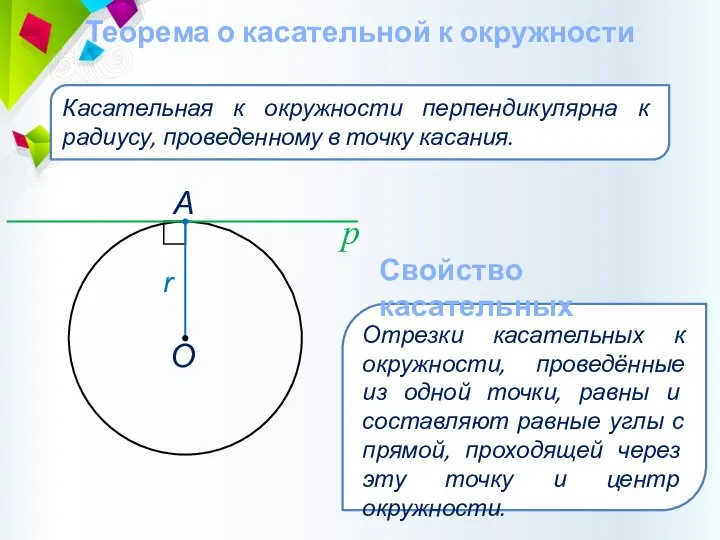
Теорема о касательной к окружности
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Свойство касательных

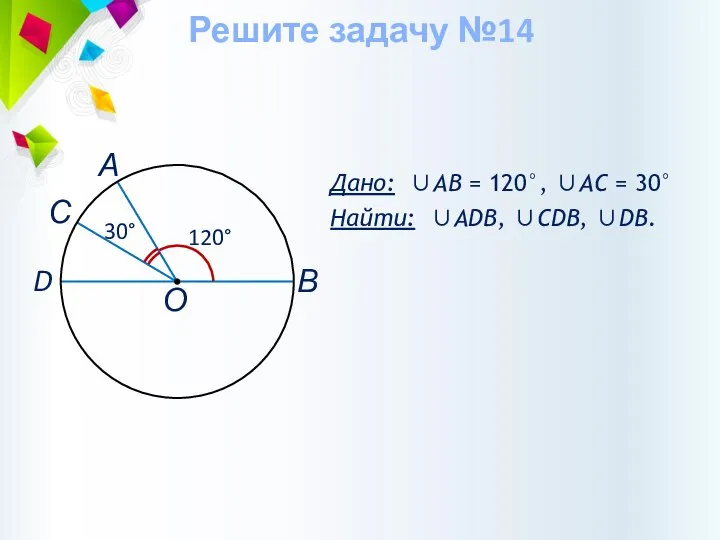
Дано: ∪АВ = 120°, ∪AC = 30°
Найти: ∪АDВ, ∪CDB, ∪DB.
Решите задачу №14

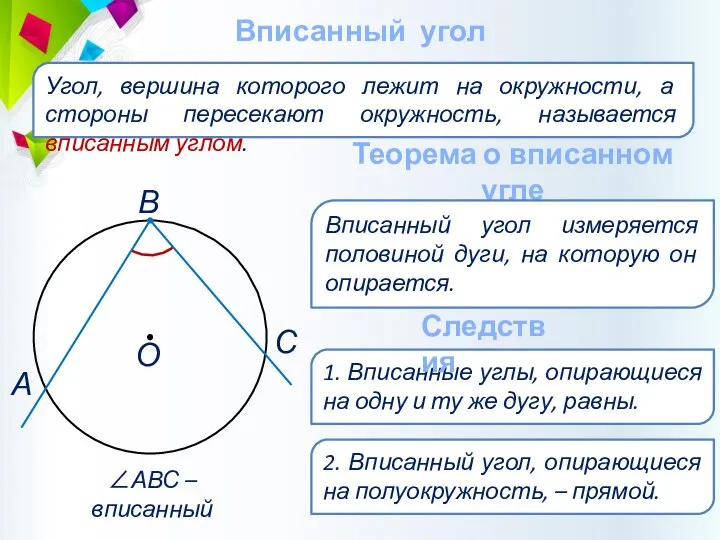
Вписанный угол
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
∠АВС – вписанный
Теорема о вписанном угле
Вписанный угол измеряется половиной дуги, на которую он опирается.
1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Следствия
2. Вписанный угол, опирающиеся на полуокружность, – прямой.

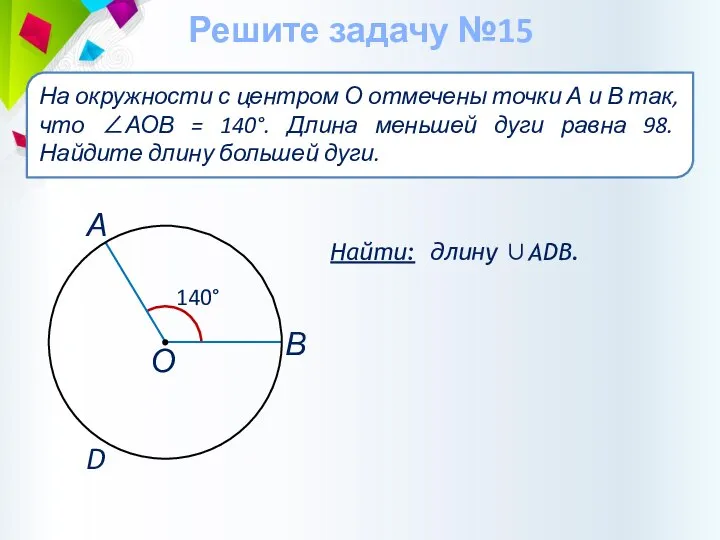
Найти: длину ∪АDВ.
На окружности с центром О отмечены точки А и В так, что ∠АОВ = 140°. Длина меньшей дуги равна 98. Найдите длину большей дуги.
Решите задачу №15

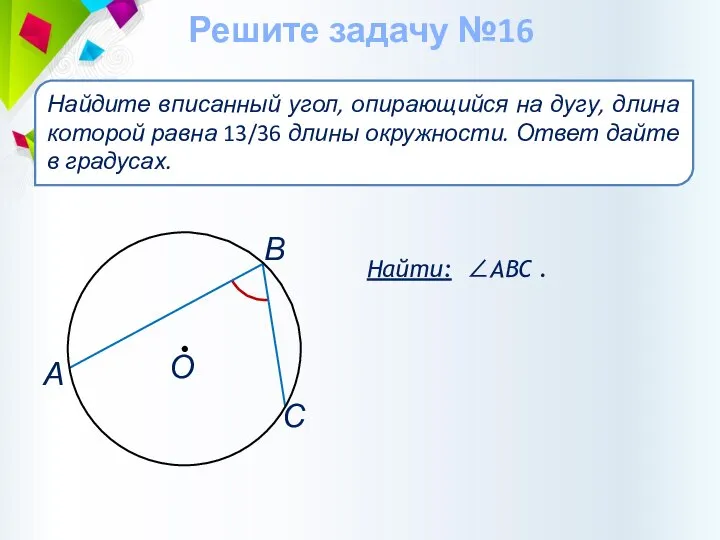
Найти: ∠АВС .
Найдите вписанный угол, опирающийся на дугу, длина которой равна 13/36 длины окружности. Ответ дайте в градусах.
Решите задачу №16