Содержание
- 2. I Müasir texnikanın bir çox nəzəri və tətbiqi məsələləri xüsusi törəməli diferensial tənliklərlə ifadə olunur. Bu
- 3. II 1) 2) 3) 4) Burada verilmiş funksiyalardır. Hesab edirik ki, verilmiş oblastın daxilində u(x,y) funksiyası
- 4. III Bunları (14.1) və (14.2)-də nəzərə alaq: (1.3) (1.4) Diferensial tənliklərin belə aproksimasiyası zamanı xəta olur.
- 5. IV l=h olan halda bu sistem aşağıdakı kimi olar: (1.5) i=0,1,2,...,n-1, j=0,1,2,...,m-1. Beləliklə, verilmiş düzbucaqlı oblastda
- 6. V Yuxarıdaki düsturda “s” – iterasiyaların nömrəsini göstərir. şərtində ardıcıllığı (1.5) sisteminin dəqiq həllinə yığılır. İterasiya
- 7. VI 3) 4)
- 9. Скачать презентацию






 Определение знаков коэффициентов K и b в линейной функции по их графикам
Определение знаков коэффициентов K и b в линейной функции по их графикам Графы
Графы Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ
Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ  Векторная алгебра
Векторная алгебра Презентация на тему Геометрическая прогрессия и ее свойство
Презентация на тему Геометрическая прогрессия и ее свойство  Логарифм
Логарифм Аттестационная работа. Решение сложных задач по математике
Аттестационная работа. Решение сложных задач по математике Головоломки и занимательные задачи
Головоломки и занимательные задачи 1_1_matritsy (1)
1_1_matritsy (1) Иллюстрации географических объектов на Луне
Иллюстрации географических объектов на Луне Подобие треугольников. Первый признак подобия
Подобие треугольников. Первый признак подобия Презентация на тему Призма и ее свойства
Презентация на тему Призма и ее свойства  Кратные интегралы
Кратные интегралы Параллельные прямые. Практическая работа
Параллельные прямые. Практическая работа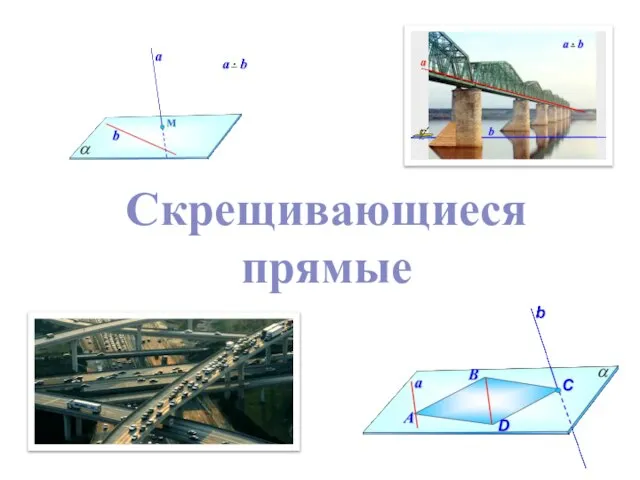 Скрещивающиеся прямые
Скрещивающиеся прямые Плоские деревья и числа Каталана
Плоские деревья и числа Каталана Упрощение логических операций
Упрощение логических операций Прямоугольные треугольники
Прямоугольные треугольники Презентация на тему Проценты
Презентация на тему Проценты  Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Математический анализ. Лекция 1
Математический анализ. Лекция 1 Движение. Поворот
Движение. Поворот Случаи вычитания 11-
Случаи вычитания 11- Слагаемое. Сумма. 1 класс
Слагаемое. Сумма. 1 класс Блез Паскаль
Блез Паскаль Знаки препинания в сложном предложении
Знаки препинания в сложном предложении Выполни вычисления
Выполни вычисления Индивидуальные задания. Урок 15
Индивидуальные задания. Урок 15