Preobrazovanie_grafikov_chislovykh_funktsiy

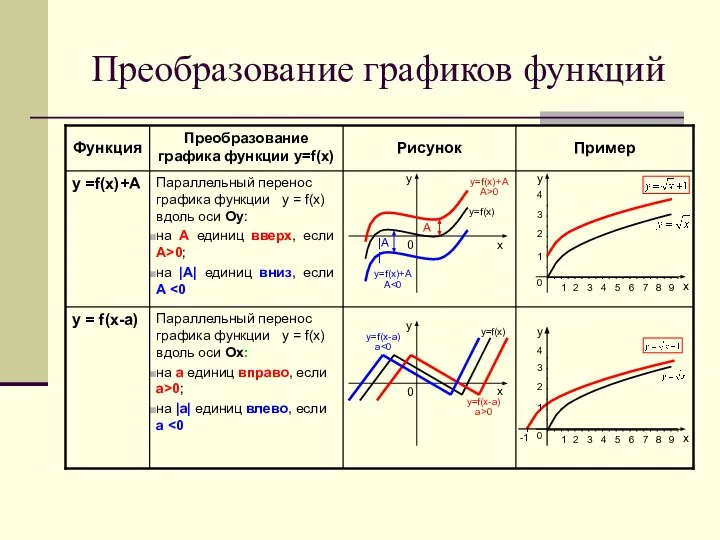
Преобразование графиков функций
Параллельный перенос графика функции у = f(х) вдоль оси Ох:
на а единиц вправо, если а>0;
на |а| единиц влево, если а <0
у = f(х-a)
Параллельный перенос графика функции у = f(х) вдоль оси Оу:
на А единиц вверх, если А>0;
на |А| единиц вниз, если А <0
у =f(х)+А
Пример
Рисунок
Преобразование графика функции у=f(x)
Функция
у
А
у=f(х)
у=f(х)+А
А>0
|А|
у=f(х)+А
А<0
0
х
у
1
2
3
0
4
у
0
х
у=f(х-а)
а>0
у=f(х)
у=f(х-а)
а<0
у
0
1
2
3
4
-1

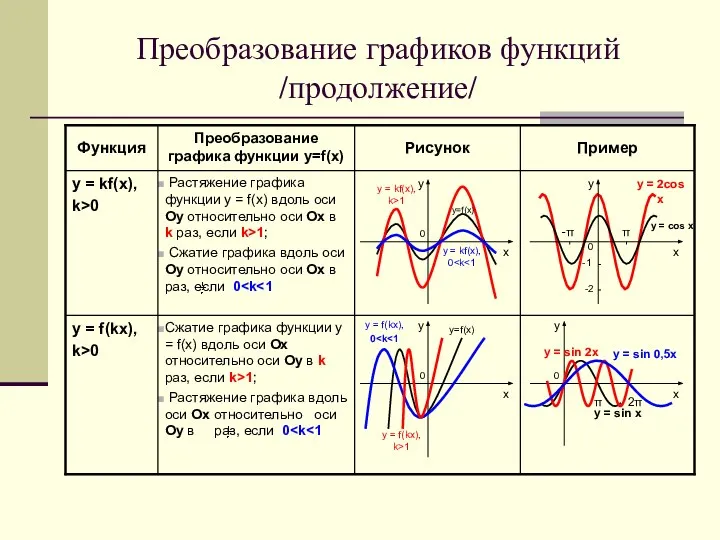
Преобразование графиков функций /продолжение/
Сжатие графика функции у = f(х) вдоль оси Ох относительно оси Оу в k раз, если k>1;
Растяжение графика вдоль оси Ох относительно оси Оу в раз, если 0
у = f(kх),
k>0
Растяжение графика функции у = f(х) вдоль оси Оу относительно оси Ох в k раз, если k>1;
Сжатие графика вдоль оси Оу относительно оси Ох в раз, если 0
у = kf(х),
k>0
Пример
Рисунок
Преобразование графика функции у=f(x)
Функция
у
х
0
у=f(х)
у = kf(х),
k>1
у = kf(х),
0
х
0
у
у=f(х)
у = f(kх),
k>1
у = f(kх),
0
х
0
у
у = cos x
у = 2cos x
π
-π
-2
-1
х
0
у
у = sin 0,5x
у = sin 2x
у = sin х
π
2π

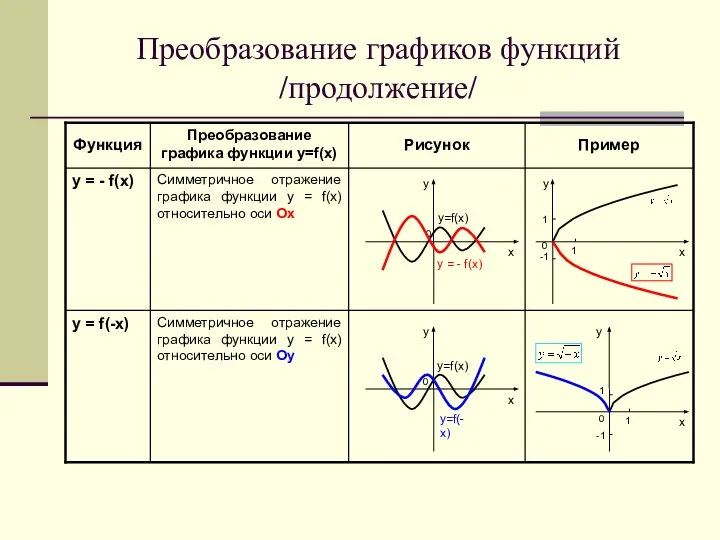
Преобразование графиков функций /продолжение/
Симметричное отражение графика функции у = f(х) относительно оси Оу
у = f(-х)
Симметричное отражение графика функции у = f(х) относительно оси Ох
у = - f(х)
Пример
Рисунок
Преобразование графика функции у=f(x)
Функция
х
0
у
у=f(х)
у = - f(х)
х
у
0
у=f(х)
у=f(-х)
х
у
0
х
у
0
1
1
-1
-1
1
1

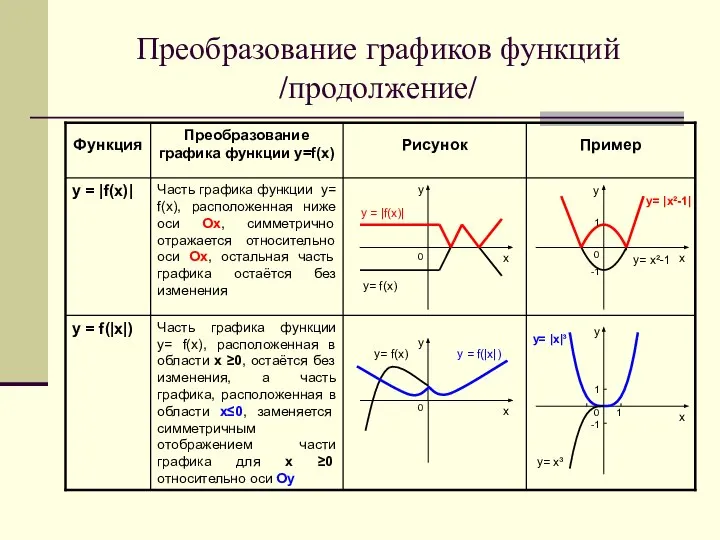
Преобразование графиков функций /продолжение/
Часть графика функции у= f(х), расположенная в области х ≥0, остаётся без изменения, а часть графика, расположенная в области х≤0, заменяется симметричным отображением части графика для х ≥0 относительно оси Оу
у = f(|х|)
Часть графика функции у= f(х), расположенная ниже оси Ох, симметрично отражается относительно оси Ох, остальная часть графика остаётся без изменения
у = |f(х)|
Пример
Рисунок
Преобразование графика функции у=f(x)
Функция
х
у
0
у= f(х)
у = |f(х)|
х
у
0
у= f(х)
у = f(|х|)
х
0
у= х²-1
у= |х²-1|
у
1
-1
х
0
у
1
-1
1
у= |х|³
у= х³

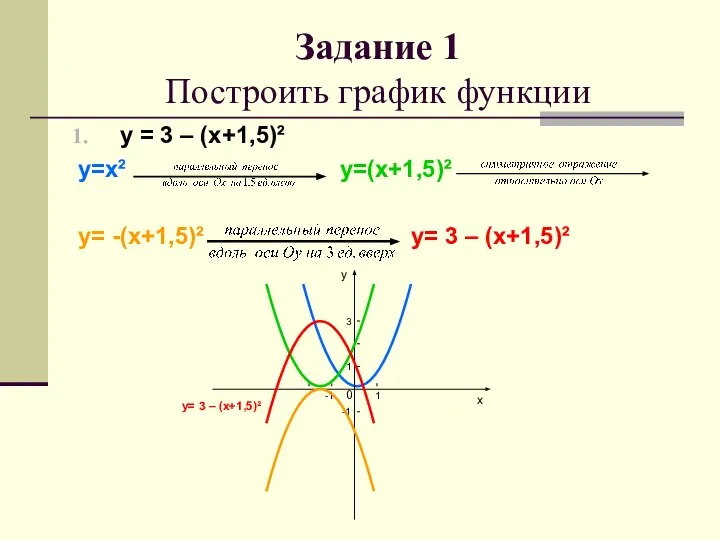
Задание 1
Построить график функции
у = 3 – (х+1,5)²
у=х² у=(х+1,5)²
у= -(х+1,5)² у= 3 – (х+1,5)²
у
х
0
1
1
-1
-1
3
у= 3 – (х+1,5)²

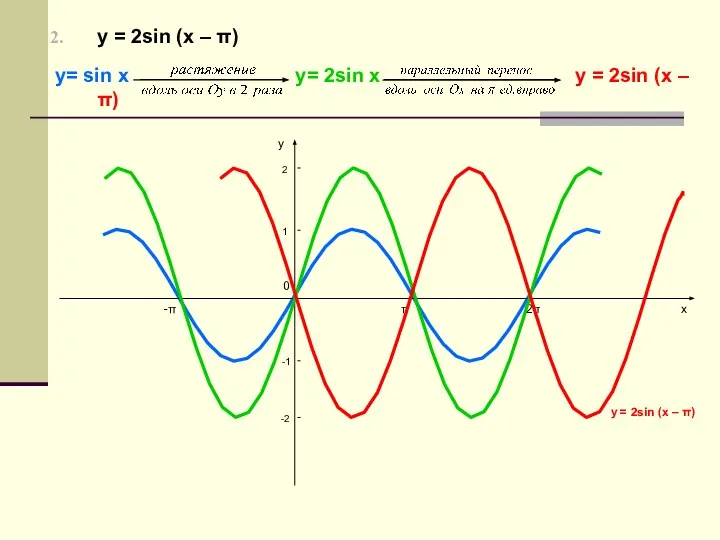
у = 2sin (х – π)
у= sin х у= 2sin х у = 2sin (х – π)
у
х
0
-1
1
π
2π
-π
2
-2
у = 2sin (х – π)