лаб7

Интегрирование
Применения: при вычислении площадей и объемов, значений работы, произведенной некоторыми силами, и т.д.
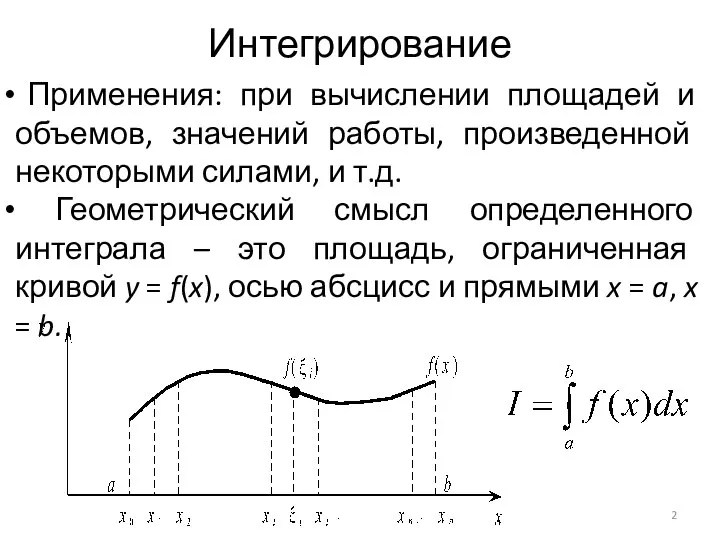
Геометрический смысл определенного интеграла – это площадь, ограниченная кривой y = f(x), осью абсцисс и прямыми x = a, x = b.

Для некоторых классов аналитически заданных функций f(x), определенный интеграл можно вычислить непосредственно, т.е. найти первообразную и воспользоваться формулой Ньютона-Лейбница:
На практике это случается редко. Чаще всего:
а) не удается выразить первообразную F(x) через элементарные функции, б) не всегда ответ удобен для использования, в) иногда значения f(x) заданы лишь в табличной форме.

Численный подход
Поэтому для решения поставленной задачи приходится использовать методы численного интегрирования, общая суть которых состоит в замене подынтегральной функции на такую аппроксимирующую функцию, чтобы интеграл от нее можно было легко найти в элементарных функциях. Чаще всего в качестве аппроксимирующих функций берут некоторые интерполяционные многочлены.
Основная идея численного интегрирования заложена уже в известном определении интеграла по Риману.

Интеграл по Риману
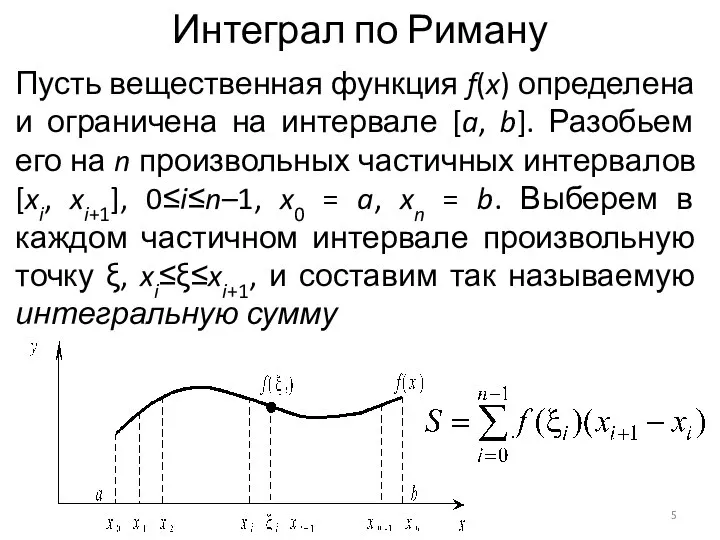
Пусть вещественная функция f(x) определена и ограничена на интервале [a, b]. Разобьем его на n произвольных частичных интервалов [xi, xi+1], 0≤i≤n–1, x0 = a, xn = b. Выберем в каждом частичном интервале произвольную точку ξ, xi≤ξ≤xi+1, и составим так называемую интегральную сумму

Если предел S при стремлении длины наибольшего частичного интервала к нулю существует для произвольных ξi, то его называют интегралом Римана от функции f(x):
На практике нельзя взять бесконечно малые длины отрезков. Но если взять их достаточно малыми, то искомый интеграл можно приблизительно заменить интегральной суммой. По существу, в этом и состоит численное интегрирование.

Формулы численного интегрирования
Существующие на практике формулы численного интегрирования, по существу, отличаются от интегральной суммы только:
1) способами разбиения интервала, т.е. выбором точек xi, ξi;
2) методами ускорения сходимости суммы к точному значению;
3) оценкой погрешности.

Квадратурная формула
Представим интегральную сумму в более общем виде. Заменим коэффициенты (xi+1 – xi) в ней некоторыми числами qi, не зависящими от f(x). Тогда
где точки a ≤ ξi ≤ b называются узлами метода, а числа qi – весами узлов.

Интеграл тогда следует записать в виде:
Эта формула называется квадратурной формулой, а R – погрешностью (остаточным членом) квадратурной формулы.
Её смысл фактически состоит в замене функции некоторым интерполяционным многочленом.

При рассмотрении конкретного метода численного интегрирования соответствующая ему квадратурная формула считается заданной, если указано, как выбирать узлы ξi и соответствующие веса qi, а также дана методика оценки погрешности R для определенных классов функций.
При реализации квадратурных формул в подавляющем большинстве случаев используется равномерная сетка с произвольным числом интерполяционных узлов, что определяет требования к степени используемых интерполяционных многочленов.

Чтобы не иметь дело с многочленами высоких степеней, обычно интервал интегрирования разбивают на отдельные небольшие участки, применяют рабочие формулы невысокого порядка на каждом участке и потом складывают результаты расчета и оценочные погрешности.
Приведем простейшие квадратурные формулы, сначала для отдельного малого интервала [хi, xi+1], а затем для всего интервала интегрирования [a, b] в виде так называемых составных квадратурных формул.

Формула прямоугольников
Рассмотрим малый интервал [–h/2, h/2]. Предположим, что подынтегральная функция f(x) дважды непрерывно дифференцируема. Тогда квадратурная формула запишется в виде:

Здесь взят один узел ξ = 0 и соответствующий вес q = h, что соответствует аппроксимации функции многочленом нулевой степени (константой). Полученная квадратурная формула называется формулой прямоугольников для одного шага или формулой средних:
I = h⋅f(0)
Название определяется тем, что интеграл функции на участке [–h/2, h/2] заменяется площадью прямоугольника с высотой f(0) и основанием h.

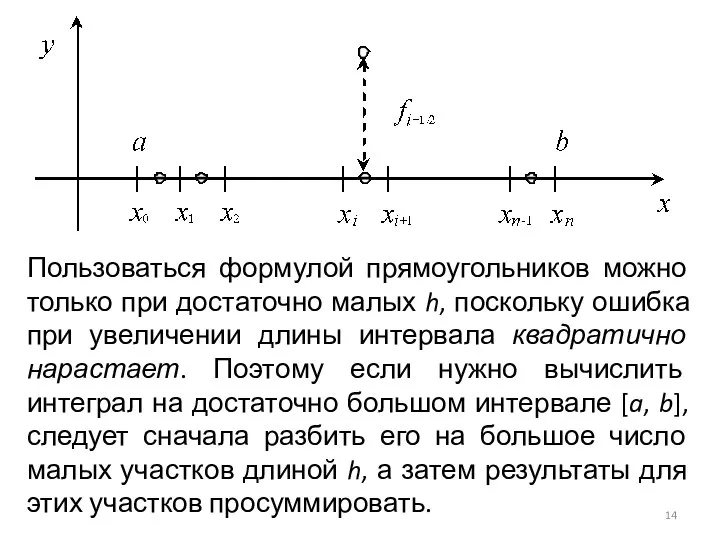
Пользоваться формулой прямоугольников можно только при достаточно малых h, поскольку ошибка при увеличении длины интервала квадратично нарастает. Поэтому если нужно вычислить интеграл на достаточно большом интервале [a, b], следует сначала разбить его на большое число малых участков длиной h, а затем результаты для этих участков просуммировать.

Тогда для i-го интервала будем иметь:
где xi ≤ ξi ≤ xi+1, 0 ≤ i ≤ n–1. Суммирование по всем интервалам приводит к составной формуле прямоугольников:
где погрешность можно оценить как (ξ ∈ [a,b])

Формула трапеций
Пусть на малом интервале [0, h] задана дважды непрерывно дифференцируемая функция f(x) ∈ C2[0,h]. Квадратурное соотношение можно записать в виде
где взяты два узла ξ0 = 0, ξ1 = h и соответствующие веса q0 = q1 = h/2, что соответствует аппроксимации функции многочленом первой степени (линейной функцией).

Получаемая квадратурная формула называется формулой трапеций для одного шага:
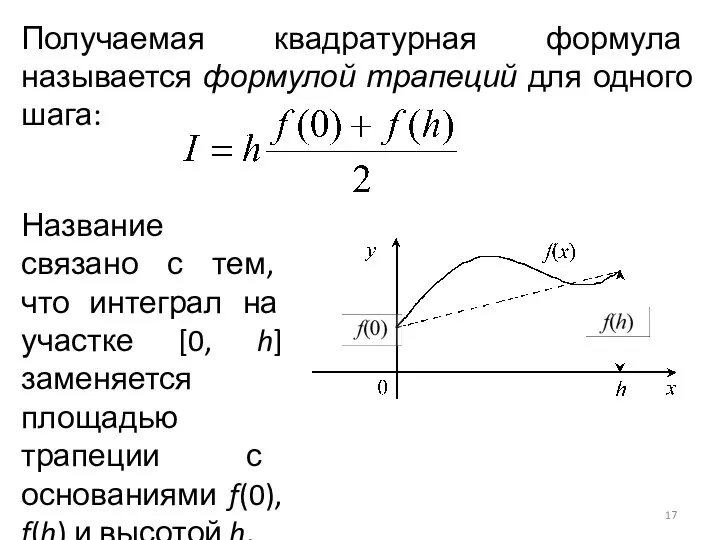
Название связано с тем, что интеграл на участке [0, h] заменяется площадью трапеции с основаниями f(0), f(h) и высотой h.

Получим формулу трапеций для полного интервала [a,b], состоящего из большого числа малых. Обозначим значение функции f(х) в узлах xi как fi=f(хi).

Тогда по аналогии с формулой для прямоугольников получим составную квадратурную формулу трапеций:

Формула парабол (Симпсона)
Возьмем малый интервал [–h, h], на котором определена четырежды дифференцируемая функция. В квадратурном соотношении возьмем три узла ξ0 = xi–1 = –h, ξ1 = xi =0, ξ2 = xi+1 =h.
Соответствующие весовые коэффициенты получим из аппроксимации f(x) параболой, построенной на точках (–h, f(–h)), (0, f(0)), (h, f(h)) в виде многочлена второй степени:
y = ax2 + bx + c

Для получения коэффициентов a, b и c построим многочлен Лагранжа второй степени, проходящий через выбранные точки:

Вычисляя интеграл, получаем при соответствующих членах значения весов. Тогда квадратурная формула для этого случая примет вид
Она называется формулой Симпсона или формулой парабол.

Для вычисления интеграла на большом интервале [a, b] разобьем его на четное число малых интервалов 2m = (b – a)/h.
Для отдельного интервала:

Суммируя по всем интервалам, получим составную формулу Симпсона:

Задание
Вычислить интеграл по формуле:
а) прямоугольника,
б) трапеций,
в) Симпсона.