Содержание
- 2. Результат теста Верно: 14 Ошибки: 0 Отметка: 5 Время: 0 мин. 27 сек. ещё
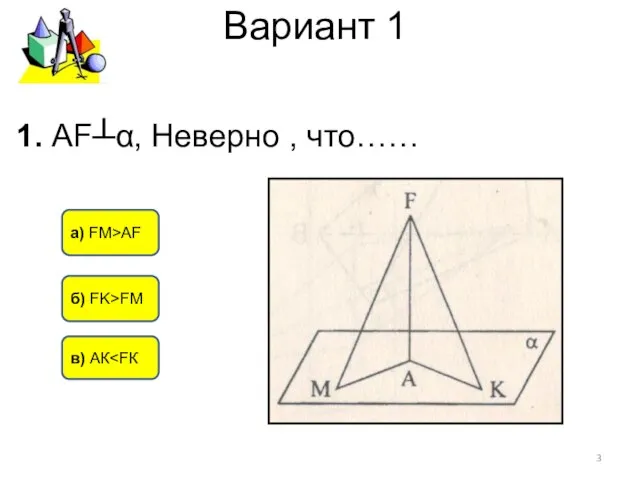
- 3. Вариант 1 б) FK>FM а) FM>AF в) АК 1. АF┴α, Неверно , что……
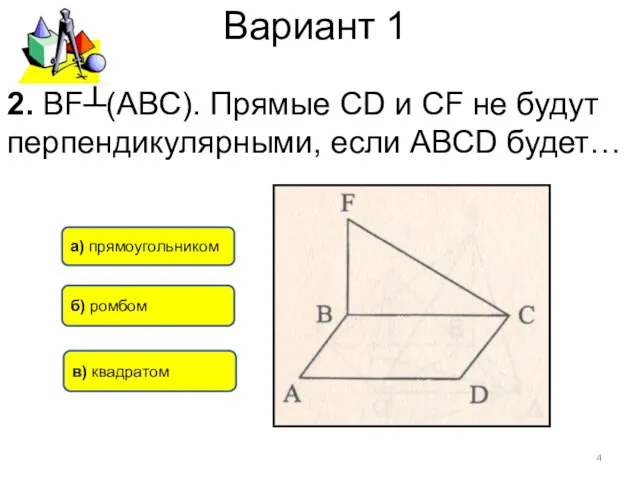
- 4. Вариант 1 2. ВF┴(АВС). Прямые СD и CF не будут перпендикулярными, если АВСD будет… б) ромбом
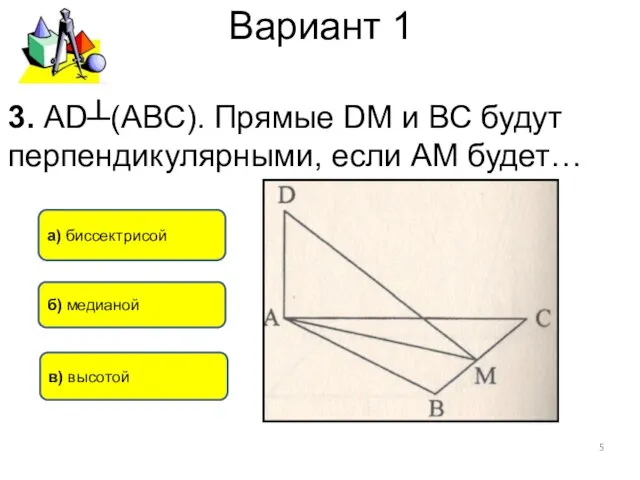
- 5. Вариант 1 в) высотой а) биссектрисой б) медианой 3. АD┴(АВС). Прямые DM и ВС будут перпендикулярными,
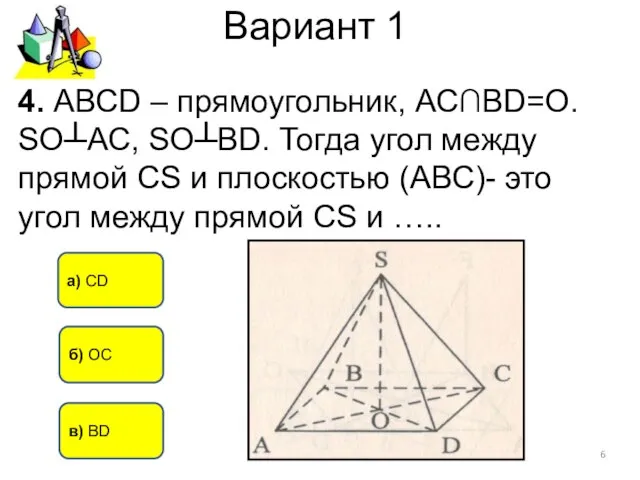
- 6. Вариант 1 б) ОС а) СD 4. АВСD – прямоугольник, АС∩BD=О. SO┴АС, SO┴BD. Тогда угол между
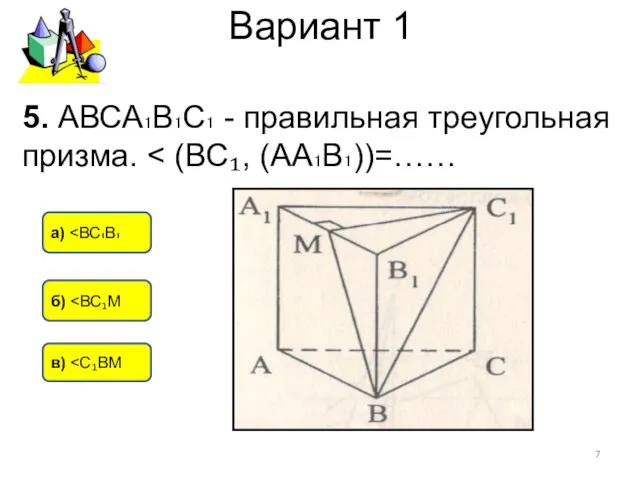
- 7. Вариант 1 в) б) а) 5. АВСА₁В₁С₁ - правильная треугольная призма.
- 8. Вариант 1 в) серединных перпендикуляров б) биссектрис углов треугольника а) высот треугольника 6. Точка М равноудалена
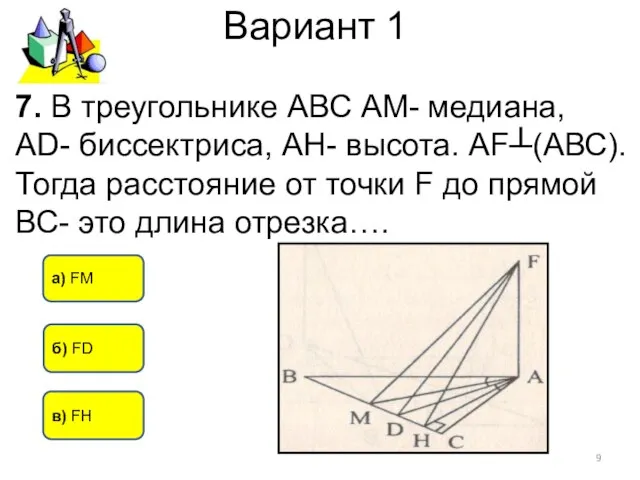
- 9. Вариант 1 7. В треугольнике АВС АМ- медиана, АD- биссектриса, АН- высота. АF┴(АВС). Тогда расстояние от
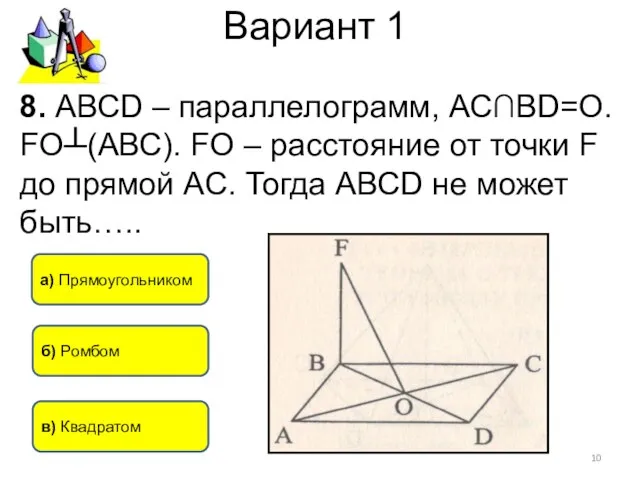
- 10. Вариант 1 8. АВСD – параллелограмм, АС∩ВD=О. FO┴(АВС). FO – расстояние от точки F до прямой
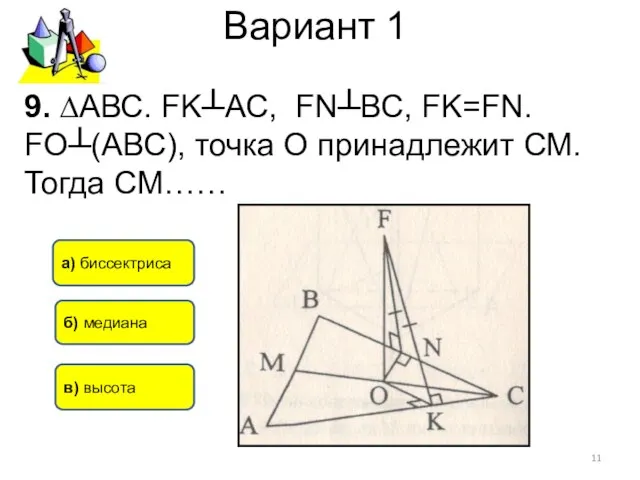
- 11. Вариант 1 9. ∆АВС. FK┴АС, FN┴ВС, FK=FN. FО┴(АВС), точка О принадлежит СМ. Тогда СМ…… а) биссектриса
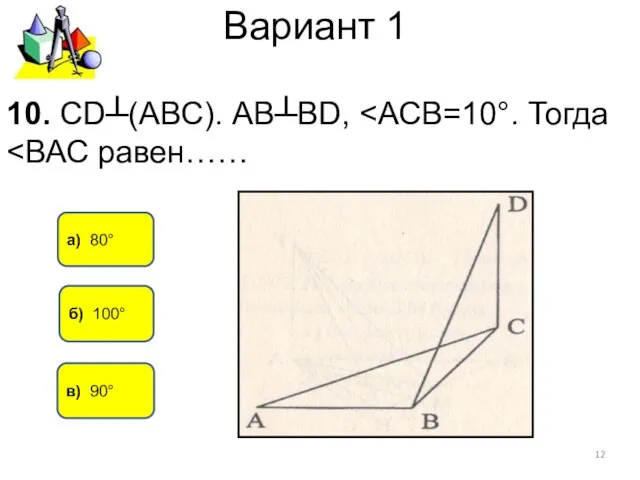
- 12. Вариант 1 а) 80° в) 90° 10. СD┴(АВС). АВ┴BD, б) 100°
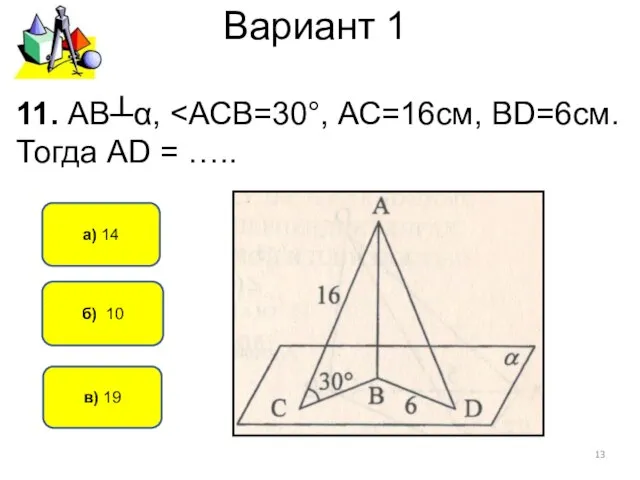
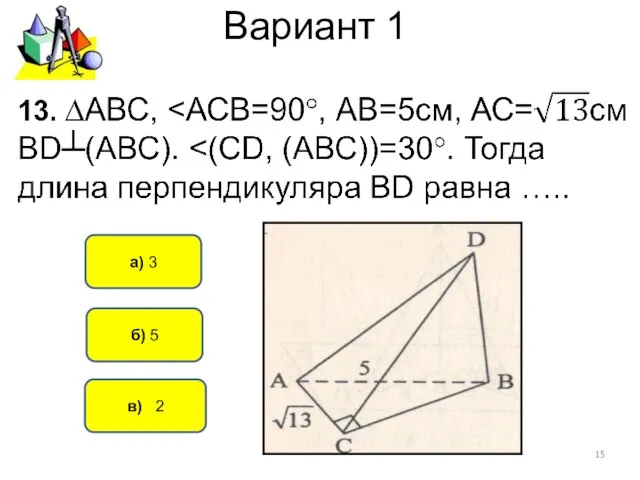
- 13. Вариант 1 б) 10 а) 14 11. АВ┴α, в) 19
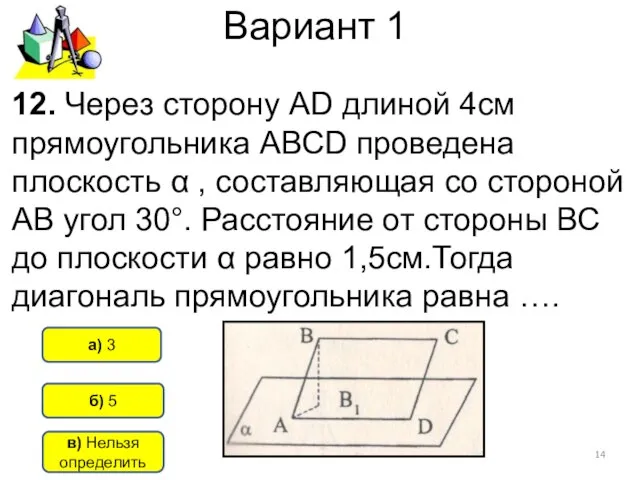
- 14. Вариант 1 б) 5 а) 3 12. Через сторону АD длиной 4см прямоугольника АВСD проведена плоскость
- 15. Вариант 1 в) 2 а) 3 б) 5
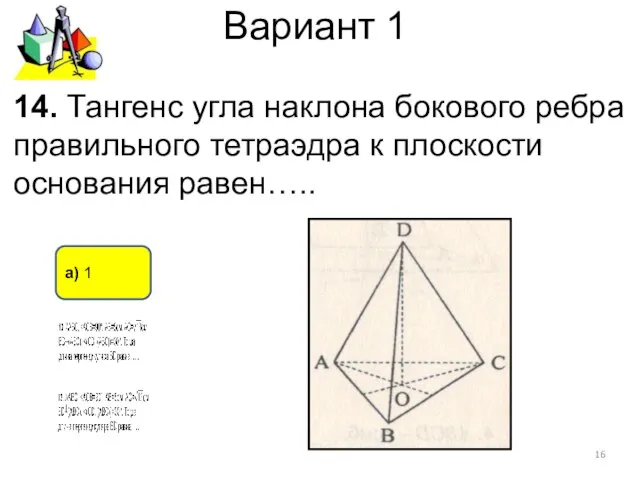
- 16. Вариант 1 а) 1 14. Тангенс угла наклона бокового ребра правильного тетраэдра к плоскости основания равен…..
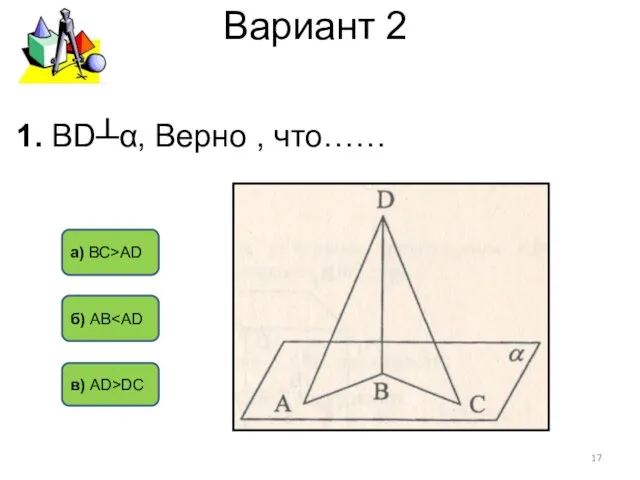
- 17. Вариант 2 б) АВ а) ВС>АD в) AD>DC 1. ВD┴α, Верно , что……
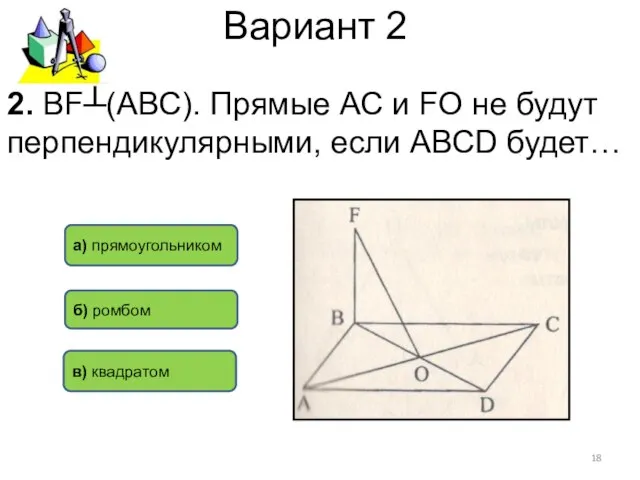
- 18. Вариант 2 2. ВF┴(АВС). Прямые АС и FО не будут перпендикулярными, если АВСD будет… а) прямоугольником
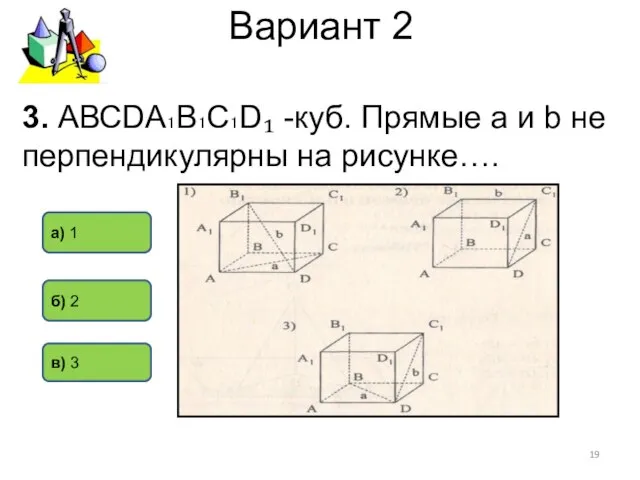
- 19. Вариант 2 в) 3 б) 2 а) 1 3. АВСDА₁В₁С₁D₁ -куб. Прямые а и b не
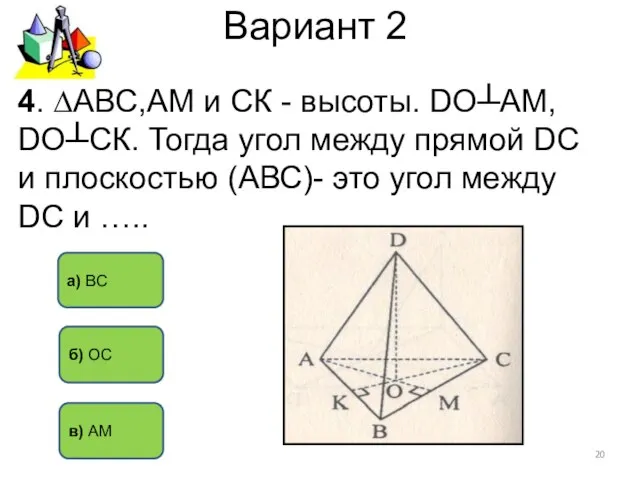
- 20. Вариант 2 б) ОС а) ВС 4. ∆АВС,АМ и СК - высоты. DO┴АМ, DO┴СК. Тогда угол
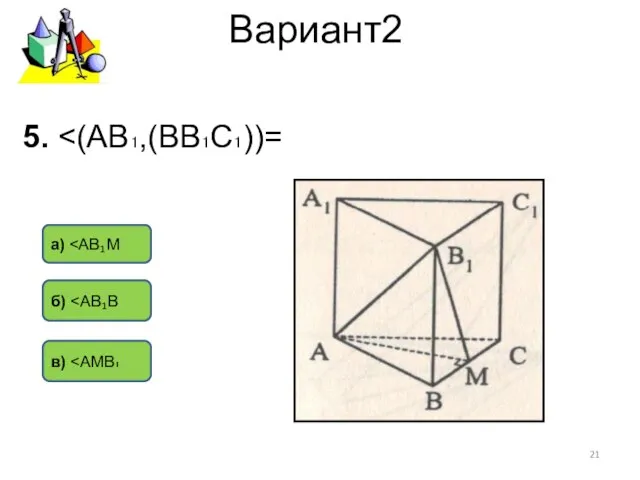
- 21. Вариант2 а) б) в) 5.
- 22. Вариант 12 б) центр описанной около ∆АВС окружности в) центр вписанной в ∆АВС окружности а) точка
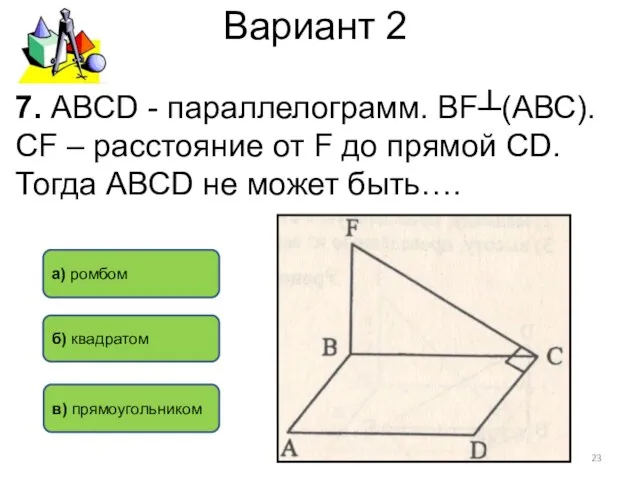
- 23. Вариант 2 7. АВСD - параллелограмм. ВF┴(АВС). СF – расстояние от F до прямой СD. Тогда
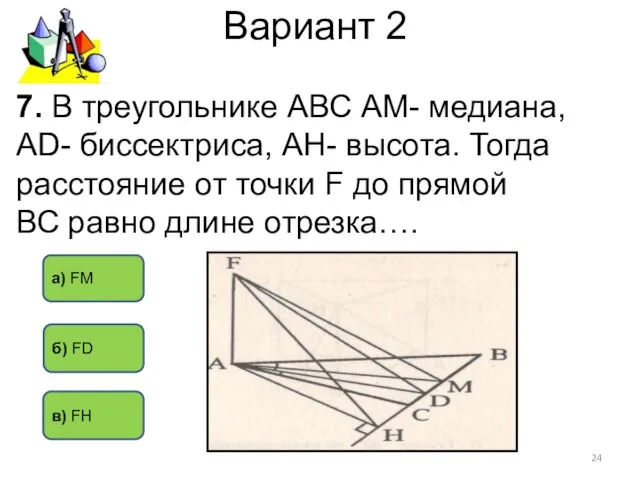
- 24. Вариант 2 7. В треугольнике АВС АМ- медиана, АD- биссектриса, АН- высота. Тогда расстояние от точки
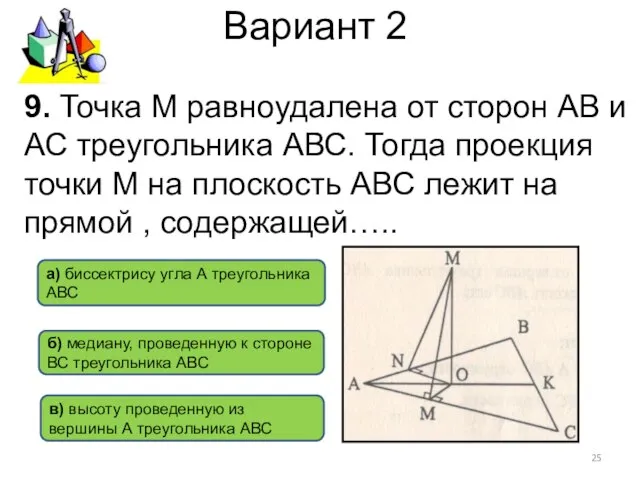
- 25. Вариант 2 9. Точка М равноудалена от сторон АВ и АС треугольника АВС. Тогда проекция точки
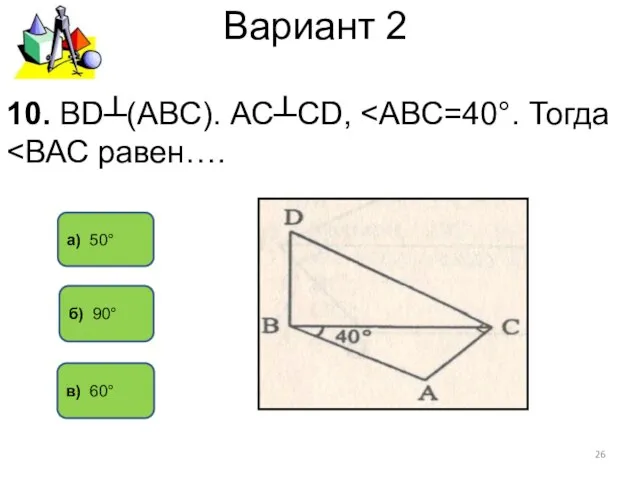
- 26. Вариант 2 а) 50° в) 60° 10. ВD┴(АВС). АС┴СD, б) 90°
- 27. Вариант 2 в) 10 б) 14 а) 19
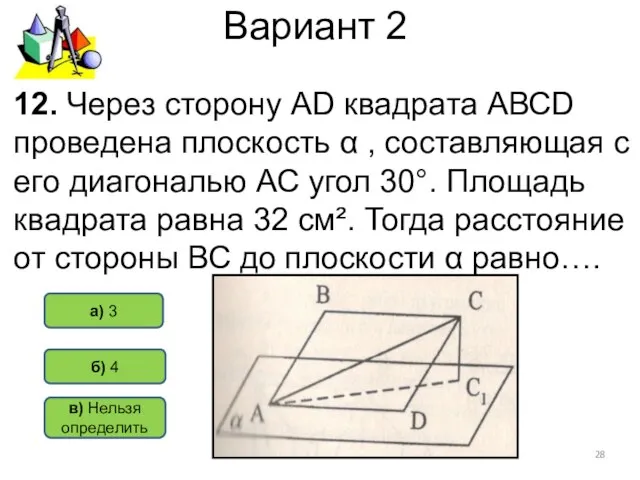
- 28. Вариант 2 б) 4 а) 3 12. Через сторону АD квадрата АВСD проведена плоскость α ,
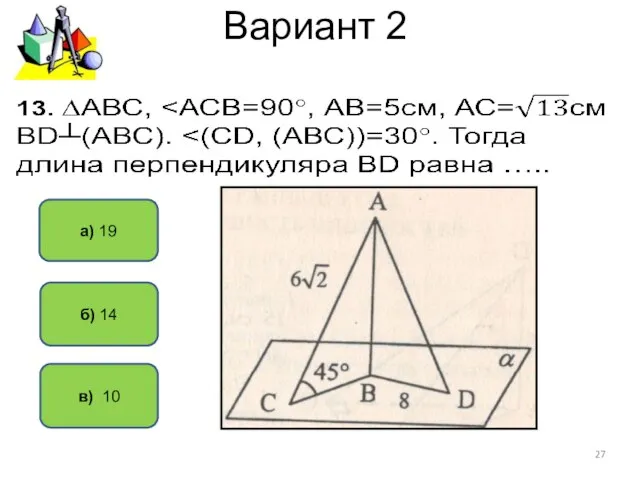
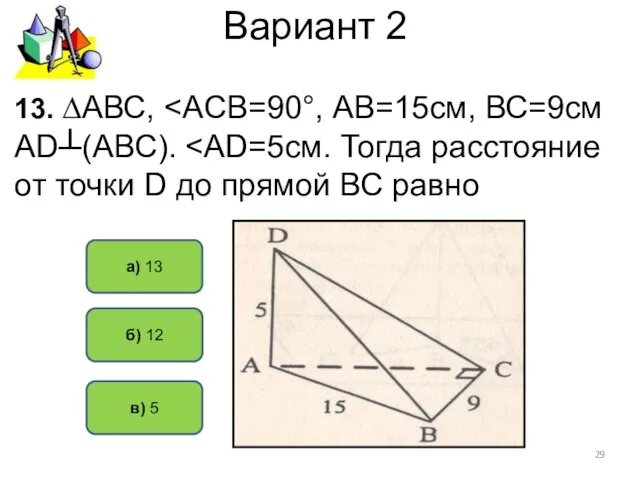
- 29. Вариант 2 а) 13 в) 5 13. ∆АВС, б) 12
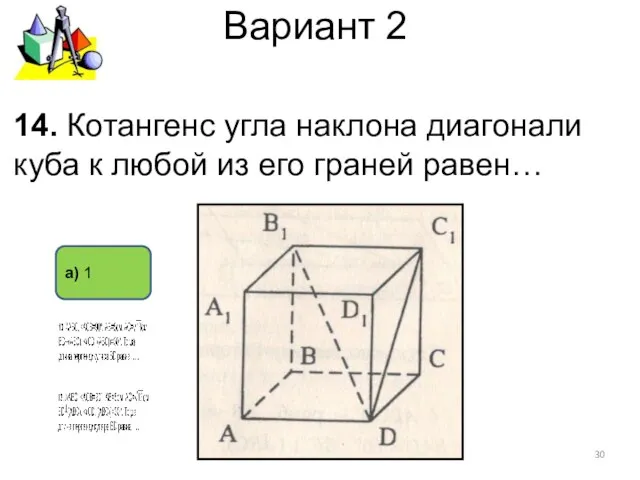
- 30. Вариант 2 а) 1 14. Котангенс угла наклона диагонали куба к любой из его граней равен…
- 31. Ключи к тесту: Перпендикуляр и наклонные. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Литература
- 33. Скачать презентацию



 Уравнение как способ перевода условия задачи на математический язык
Уравнение как способ перевода условия задачи на математический язык Длина окружности. Площадь круга
Длина окружности. Площадь круга Корень n-ой степени
Корень n-ой степени Ортогональная проекция плоской фигуры на плоскость и ее площадь
Ортогональная проекция плоской фигуры на плоскость и ее площадь Стереометрия в задачах ЕГЭ
Стереометрия в задачах ЕГЭ Методы прогнозирования потерь в осевых турбинах
Методы прогнозирования потерь в осевых турбинах Прямая. Ортогональные проекции прямой линии
Прямая. Ортогональные проекции прямой линии Измерение длины отрезка
Измерение длины отрезка Случайные величины
Случайные величины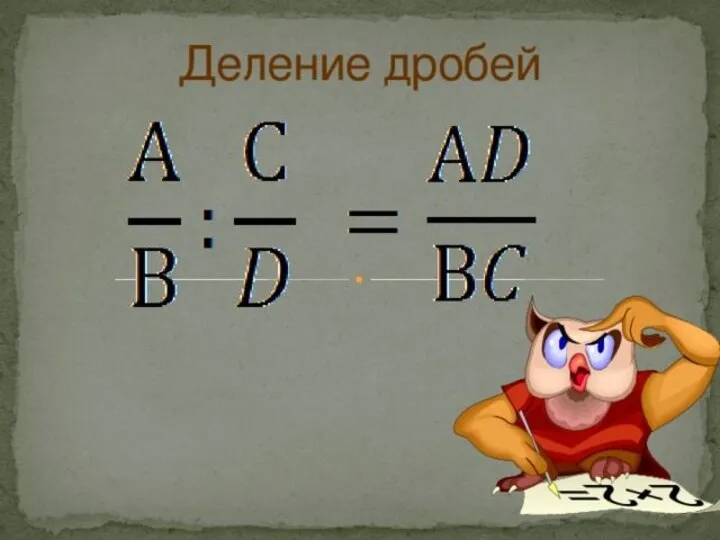 Деление дробей
Деление дробей Тест. Свойство простейших фигур
Тест. Свойство простейших фигур Многогранник с двумя основаниями
Многогранник с двумя основаниями Вычисление пределов функций
Вычисление пределов функций 20120818_pryamaya_i_obratnaya_proporcionalnost
20120818_pryamaya_i_obratnaya_proporcionalnost Расчетное задание
Расчетное задание Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Презентация на тему Решение задач различными способами
Презентация на тему Решение задач различными способами  Первообразная. 11 класс
Первообразная. 11 класс Анализ работы.12 задач
Анализ работы.12 задач Задачи на построение
Задачи на построение Векторы
Векторы Числа и точки на прямой. 5 класс
Числа и точки на прямой. 5 класс Раз, два, три. Спортивно-математический турнир
Раз, два, три. Спортивно-математический турнир Применение синуса и косинуса при программировании движения с поворотом. Для учащихся 7-8 классов
Применение синуса и косинуса при программировании движения с поворотом. Для учащихся 7-8 классов Деление на 2
Деление на 2 Решение комбинаторных задач
Решение комбинаторных задач Лабораторно-практическая работа в парах
Лабораторно-практическая работа в парах Решение уравнений «В мире звезд»
Решение уравнений «В мире звезд»