Презентация на тему Цилиндр

Введение.
Основная часть.
Что называют цилиндром? (из истории).
Различные определения.
Выпуклый цилиндр.
Свойства цилиндра.
Прямой цилиндр
Площадь поверхности цилиндра.
Объем цилиндра
Решение задач.
Заключительная часть.
Используемая литература.
Краткое содержание!

Виды цилиндра!
Цилиндрическая поверхность
Круговой цилиндр
Прямой цилиндр

Свойства цилиндра.
1) Основания равны и параллельны
2) Все образующие цилиндра параллельны и равны друг другу
3) все высоты цилиндра параллельны и равны друг другу.
Перпендикуляр, опущенный из любой точки одного основания цилиндра на плоскость другого его основания, называется высотой цилиндра.

Сечения цилиндра.
1) Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник , две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.
2) Все сечения цилиндра плоскостями параллельными плоскости основания, равны основаниям цилиндра между собой.

Эллипс как сечение цилиндра.
Если боковую поверхность цилиндра вращения пересечь плоскость так, чтобы она не пересекала его оснований, то в сечении получится эллипс. Это следует из определения эллипса как параллельной проекции окружности на плоскость.
Сумма расстояний от любой точки эллипса до двух точек, называемых фокусами, есть величина постоянная.

Площадь поверхности прямого цилиндра.
Sбок=2πrh.
Sпол. п.=2πr (r + h).

Объём цилиндра.
Объем цилиндра равен произведению площади основания на высоту.
V = πr²h.

Решение задач.
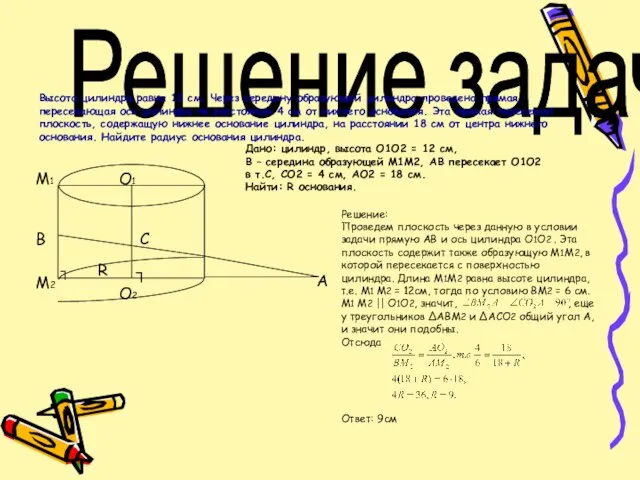
Высота цилиндра равна Н, радиус его основания равен R. В цилиндр помещена пирамида, высота которой совпадает с образующей АА1 цилиндра, а основанием служит равнобедренный треугольник АВС (АВ=АС), вписанный в основание цилиндра. Найти площадь боковой поверхности пирамиды, если А = 120°.
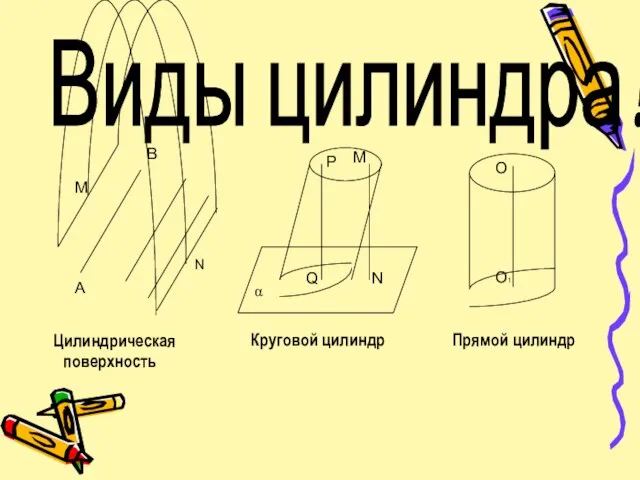
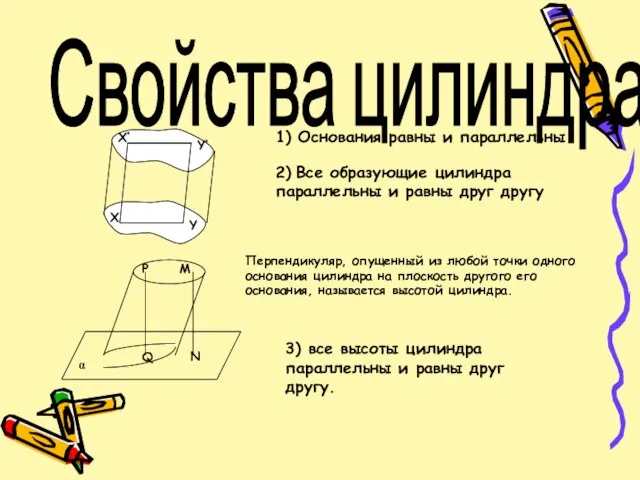
Дано: цилиндр с высотой H и радиусом R, вписана пирамида, образующая АА1 – высота пирамиды, АВС р/б, АВ=АС, АВС – вписан в основание цилиндра,
угол А = 120°.
Найти: Sбок пирамиды.
Решение:
1)Проведем AD ┴ BC и соединим точки А1 и D. Согласно теореме , имеем А1D┴ BC. Так
как дуга CAB содержит 120° , а дуги АС и АВ – по 60° , то ВС = R , АВ = R .
2)В ∆ ABD имеем AD = R/2 . Далее, из ∆AA1D получим
A1D = ½
Следовательно SА1АВ = ½ АВ · АА1 = ½ RH
SА1ВС = ½ ВС · А1D = ½ R ∙ ½ = ¼ R
3) Sбок = 2 SА1АВ + SА1ВС = RH + ¼ R =
= R/4(4H + ).
Ответ: R/4(4H + ).

Решение задач.
Высота цилиндра равна 12 см. Через середину образующей цилиндра проведена прямая, пересекающая ось цилиндра на расстоянии 4 см от нижнего основания. Эта прямая пересекает плоскость, содержащую нижнее основание цилиндра, на расстоянии 18 см от центра нижнего основания. Найдите радиус основания цилиндра.
Дано: цилиндр, высота О1О2 = 12 см,
В – середина образующей М1М2, АВ пересекает О1О2 в т.С, СО2 = 4 см, АО2 = 18 см.
Найти: R основания.