Содержание
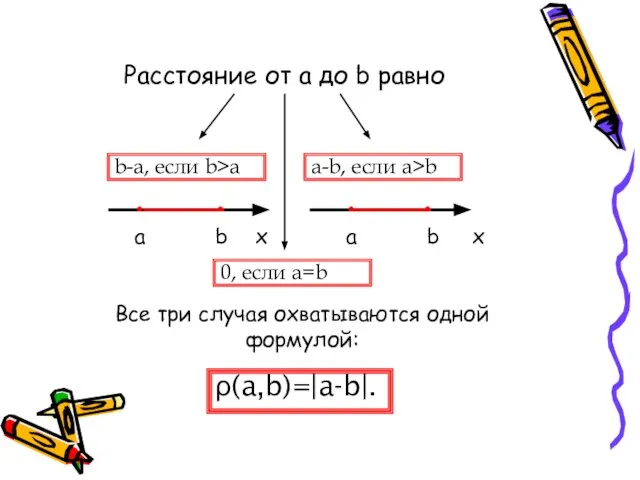
- 2. Расстояние от a до b равно х х a a b b . . . .
- 3. решим уравнения: а) |x-2|=3 Найдём на координатной прямой такие точки х, которые удовлетворяют условию ρ(х,2)-3, т.
- 4. б) |х-√2|=0 Для уравнения |х-√2|=0 можно обойтись без геометрической иллюстрации, ведь если |а|=0, то а=0. поэтому
- 5. в) |2х-6| = 8 |2х-6| = |2х(х-3)| = |2|∙|х-3| = 2|х-3|. Значит, заданное уравнение можно преобразовать
- 7. Скачать презентацию



 Решение тригонометрических уравнений
Решение тригонометрических уравнений Алгоритм вычисления алгебраических выражений
Алгоритм вычисления алгебраических выражений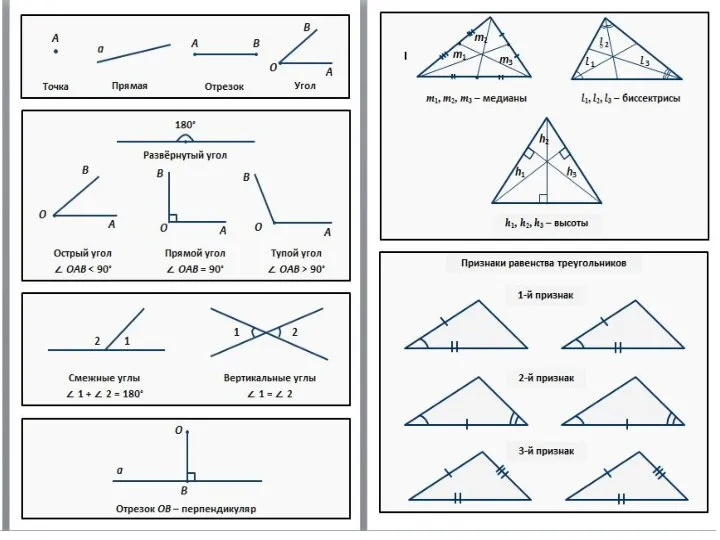 Геометрия. 8 класс
Геометрия. 8 класс Деление с остатком
Деление с остатком Понятие интеграла
Понятие интеграла Тема Функция у = ах2 и её график
Тема Функция у = ах2 и её график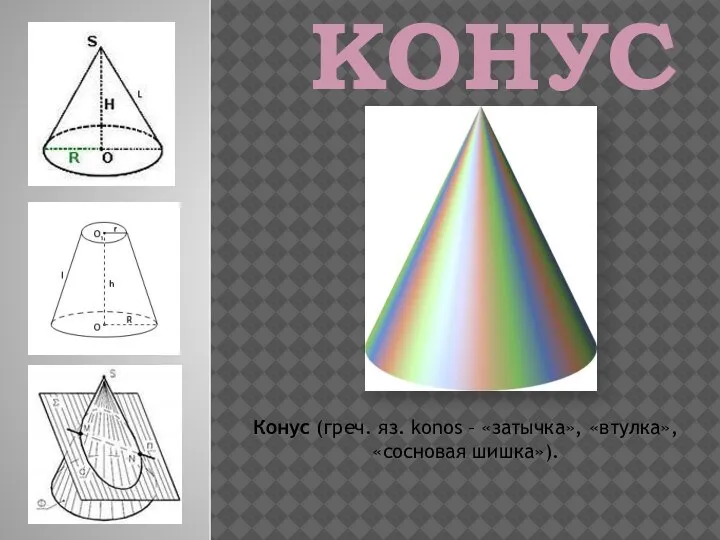 Конус. Виды конусов. Конусы в нашей жизни
Конус. Виды конусов. Конусы в нашей жизни Приближенные числа. Округление чисел. Бородино 1812 г. 26 августа (7 сентября)
Приближенные числа. Округление чисел. Бородино 1812 г. 26 августа (7 сентября) Способы решения тригонометрических уравнений
Способы решения тригонометрических уравнений polupravilnye-mnogogranniki
polupravilnye-mnogogranniki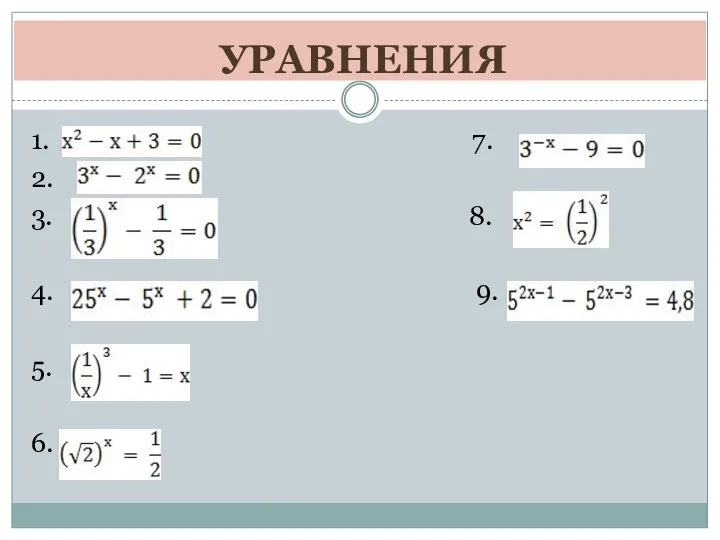 Решение показателей уравнений
Решение показателей уравнений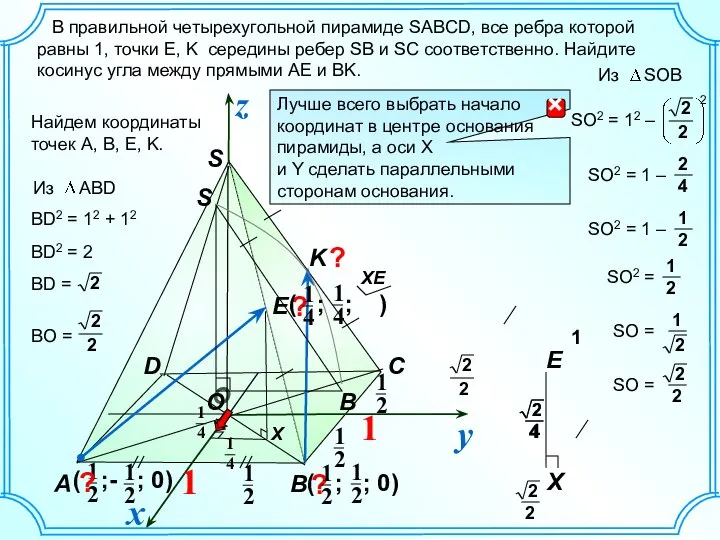 Пирамиды. Решение задач. C 12
Пирамиды. Решение задач. C 12 Примеры на сложение и вычитание
Примеры на сложение и вычитание Итоговое повторение. 9 класс (2)
Итоговое повторение. 9 класс (2) Геометрические фигуры: круг, квадрат, треугольник
Геометрические фигуры: круг, квадрат, треугольник Графы. ЕГЭ задание 15. Урок 11 А
Графы. ЕГЭ задание 15. Урок 11 А Математическая разминка
Математическая разминка Личные (семейные) финансы. Финансовое планирование и бюджет. Решение задач
Личные (семейные) финансы. Финансовое планирование и бюджет. Решение задач Вычисления с многозначными числами
Вычисления с многозначными числами Графики. График движения
Графики. График движения Движение по окружности. Подборка задач
Движение по окружности. Подборка задач Графическое оформление результатов эксперимента
Графическое оформление результатов эксперимента Введение в математический анализ и дифференциальное исчисление
Введение в математический анализ и дифференциальное исчисление Задачи на концентрацию, сплавы. Подготовка к ЕГЭ
Задачи на концентрацию, сплавы. Подготовка к ЕГЭ Сложение и вычитание в пределах 20. Повторение
Сложение и вычитание в пределах 20. Повторение Презентация по математике "Мы рады привествовать вас на уроке математики" -
Презентация по математике "Мы рады привествовать вас на уроке математики" -  Линейная алгебра. Метод Гаусса для решения систем линейных алгебраических уравнений
Линейная алгебра. Метод Гаусса для решения систем линейных алгебраических уравнений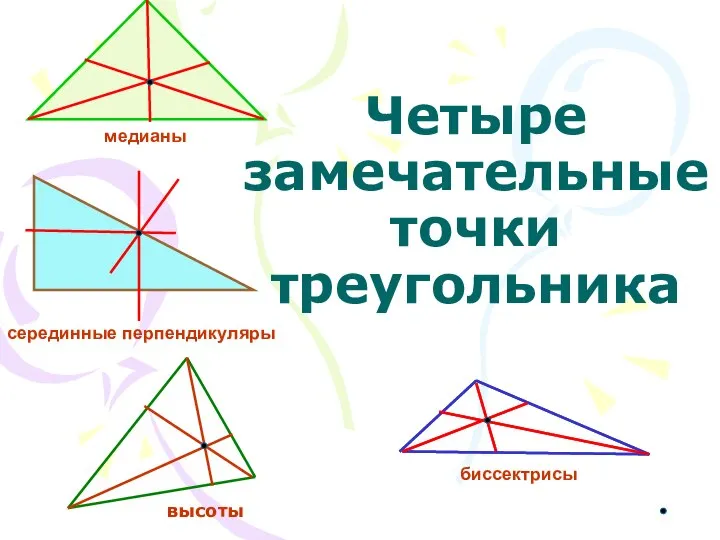 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника