Решение задач с помощью уравнений

План работы
Запишите тему урока.
Выполните тест , ответы запишите да или нет.
Разберите задачу.
Запишите этапы решения задачи.
Выполните задание на карточке.
Карточка в вордовском документе смотри сетевой или в группе.
Отправь учителю на проверку.

Верные и неверные утверждения
Корни уравнения изменяются, если обе части уравнения умножить на число (-10) .
Может ли разность двух отрицательных чисел быть целым положительным числом?
Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак
Если перед скобками стоит знак «–», то нужно раскрыть скобки, сохранив знаки слагаемых .
На ноль делить можно.
6. Чтобы сложить подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
7. Если перед скобками стоит знак «+», то можно опустить скобки, сохранив знаки слагаемых.
8. Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел и поставить «–» .
9. Произведение может быть равно нулю, когда хотя бы один из множителей равен нулю.
10. Может ли сумма двух целых положительных чисел быть равной 0?

Задача 1.
В одном бидоне молока в 3 раза больше, чем в другом. Когда из одного бидона перелили в другой 5литров, молока в бидонах стало поровну. Сколько литров молока было в каждом бидоне первоначально?

Этапы решения задачи:
Анализ задачи (условия и вопросы, число объектов).
Схематическая запись задачи (схема, таблица, краткая запись).
Запись уравнения.
Решение уравнения.
Запись ответа с учётом вопроса задачи.

Задача 1.
В одном бидоне молока в 3 раза больше, чем в другом. Когда из одного бидона перелили в другой 5литров, молока в бидонах стало поровну. Сколько литров молока было в каждом бидоне первоначально?

х
3х
3х-5
х+5
Было
1 бидон
2 бидон
Стало
Было
1
2
Стало
3х
х

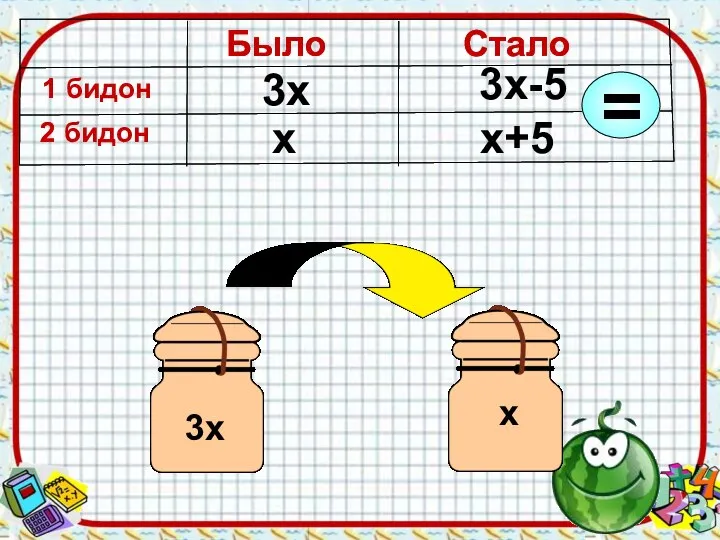
Краткое условие задачи
Пусть х литров – количество молока во втором бидоне до переливания.
3х литров – количество молока в первом бидоне до переливания;
(3х – 5) литров – осталось в первом бидоне;
(х + 5) литров – стало во втором бидоне.
По условию задачи, после переливания молока в обоих бидонах стало поровну.
Составим уравнение:
З х – 5 = х + 5

Решение уравнения
Зх – 5 = х + 5
Зх – х = 5 + 5
2х = 10
Х = 10 : 2
Х = 5
5 литров молока было во втором бидоне
3 · 5 = 15 (л) молока было в первом бидоне.
Ответ: 15л, 5л.