Презентация на тему Применение свойств функций к решению уравнений и неравенств

Содержание
Метод мажорант (метод оценки)
Использование свойств функций:
Область определения
Множество значений
Четность и нечетность
3. Задачи с параметром
4. Задачи из сборника ЕГЭ, часть «С»
5. Использованные источники

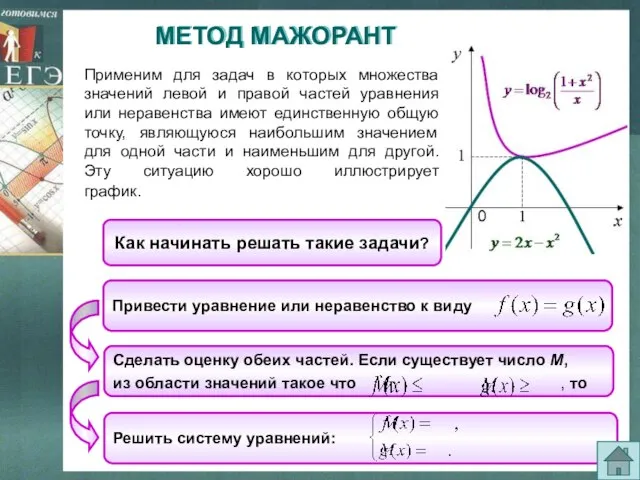
Применим для задач в которых множества значений левой и правой частей уравнения или неравенства имеют единственную общую точку, являющуюся наибольшим значением для одной части и наименьшим для другой. Эту ситуацию хорошо иллюстрирует график.
Как начинать решать такие задачи?
МЕТОД МАЖОРАНТ
Привести уравнение или неравенство к виду

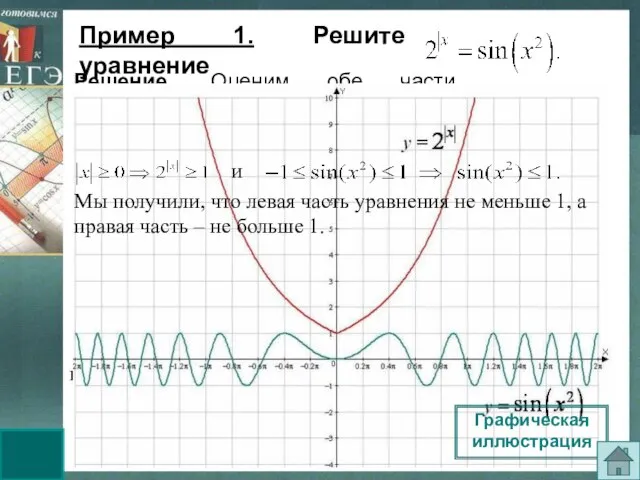
удовлетворяет второму уравнению.
Решение. Оценим обе части уравнения.
При всех значениях х верны неравенства:
Следовательно, данное уравнение равносильно системе:
Графическая иллюстрация
Мы получили, что левая часть уравнения не меньше 1, а правая часть – не больше 1.

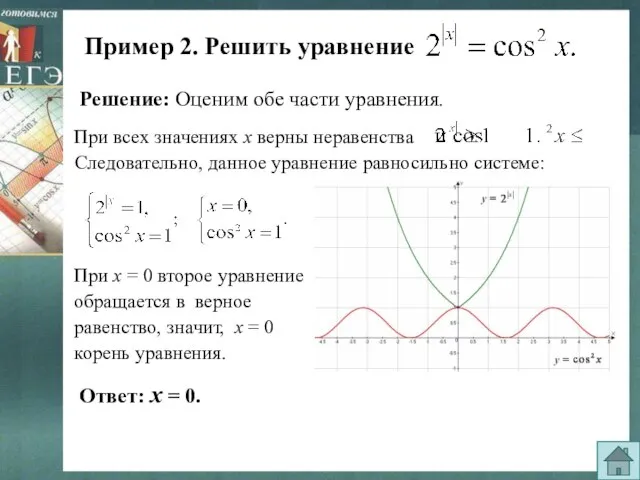
Пример 2. Решить уравнение
Решение: Оценим обе части уравнения.
Следовательно, данное уравнение равносильно системе:
При х = 0 второе уравнение обращается в верное равенство, значит, х = 0 корень уравнения.
Ответ: х = 0.

Сделаем оценку функций, входящих в неравенство.
Пример 3. Решить неравенство
Следовательно, исходное неравенство выполняется тогда и только тогда, когда оба множителя равны 1 одновременно.
Ответ: - 1.
Решение.
Получаем х = -1 – единственное решение системы уравнений, а, значит, и данного неравенства.

(так как: ).
Пример 4. Решить уравнение
Для правой части (в силу неравенства для суммы двух взаимно
обратных чисел) выполнено
Поэтому уравнение имеет решения, если и только если
одновременно выполнены два условия
принимает значение от 0,5 до 2
Решение. Оценим обе части уравнения.

Пример 5. Решить уравнение
2) Решая первое уравнение системы, находим :
3) Подставим найденные значения во второе уравнение:
Решение. Оценим обе части уравнения.
1) Каждое слагаемое левой части уравнения не больше 1, следовательно их сумма будет равна 2, если они принимают своё наибольшее значение.

Пример 6. Решить уравнение
Решение. Оценим множители левой части уравнения.
почленно эти неравенства, получаем:
Следовательно, левая часть равна правой, лишь при условии:
Значит, данное уравнение равносильно системе уравнений:
Решая систему уравнений, получаем решения исходного уравнения:
.
Заметим, что перемножив
Ответ:
?
сумма двух положительных взаимообратных чисел
?
?
сумма единицы и неотрицательного числа
sin 3z [-1;1]  3 + sin3z [2; 4].

Проверим справедливость первого равенства, подставив эти корни.
При
Пример 7. Решите уравнение
Решение. Для решения уравнения
оценим его части:
Поэтому равенство возможно
только при условии:
Сначала решим второе уравнение:
Корни этого уравнения
Итак, данное уравнение имеет единственный корень х = 0.
Ответ: 0.
При х = -1 имеем:
?
?
cos()[-1;1]  cos2( )[0; 1].
сумма единицы и неотрицательного числа.

Пример 8. Найти все значения параметра а, при каждом из которых уравнение
имеет решения. Найдите эти решения.
При всех значениях х выражение:
При всех значения х выражение:
поэтому
Следовательно, левая часть уравнения не меньше 4, а правая часть – не больше 4. Получаем систему:
Решение. Перепишем уравнение в виде
Оценим функции входящие в данное уравнение.
Очевидно, что

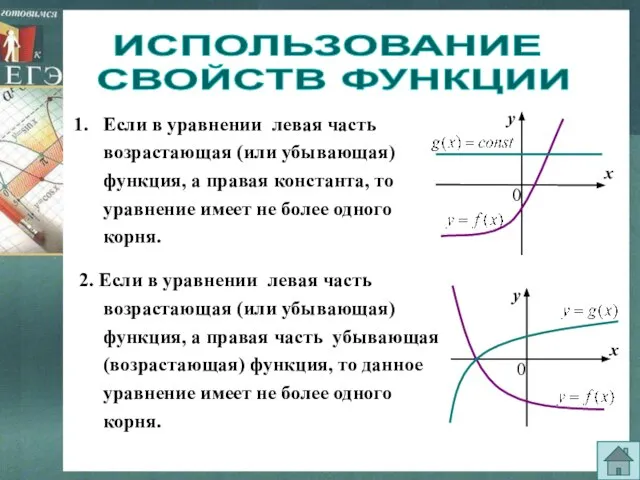
ИСПОЛЬЗОВАНИЕ
СВОЙСТВ ФУНКЦИИ
Если в уравнении левая часть возрастающая (или убывающая) функция, а правая константа, то уравнение имеет не более одного корня.
2. Если в уравнении левая часть возрастающая (или убывающая) функция, а правая часть убывающая (возрастающая) функция, то данное уравнение имеет не более одного корня.
х
у
0
х
у
0

Пример 9. Решить уравнение
Решение:
Заметим, что х = 1 , является корнем данного уравнения. Левая часть уравнения представляет собой сумму двух возрастающих функций и, следовательно, сама является возрастающей функцией, принимающей каждое своё значение ровно один раз.
Поэтому других корней данное уравнение не имеет.
Ответ: 1.

Пример 10. Доказать, что уравнение не имеет решений:
Арифметический корень не может быть отрицательным числом, поэтому уравнение решений не имеет.
?
?
?
?
?

ИСПОЛЬЗОВАНИЕ ОБЛАСТИ
ОПРЕДЕЛЕНИЯ ФУНКЦИИ
Итак, единственной точкой, в которой определены эти радикалы, является x = 1. Легко проверить, что это число – корень уравнения.
Решить уравнение:
Решение.
Второй радикал определен при любых значениях х.
Выражение под третьим радикалом неотрицательно если
Ответ: 1.

Решить уравнение
1) Выпишем, условие существования функции, стоящей в левой части:
Решить данное неравенство довольно сложно.
3) Значит, исходное уравнение тоже не имеет решений, так как левая часть его – неотрицательная функция!
Ответ: .
Решение.
2) Проверим не отрицательность правой части:
Последнее неравенство решений не имеет.

ИСПОЛЬЗОВАНИЕ СВОЙСТВА ОГРАНИЧЕННОСТИ ФУНКЦИИ
ДЛЯ НАХОЖДЕНИЯ ЕЁ НАИБОЛЬШЕГО ЗНАЧЕНИЯ
Укажите наибольшее целое значение функции
Ответ: 1250.
Решение.

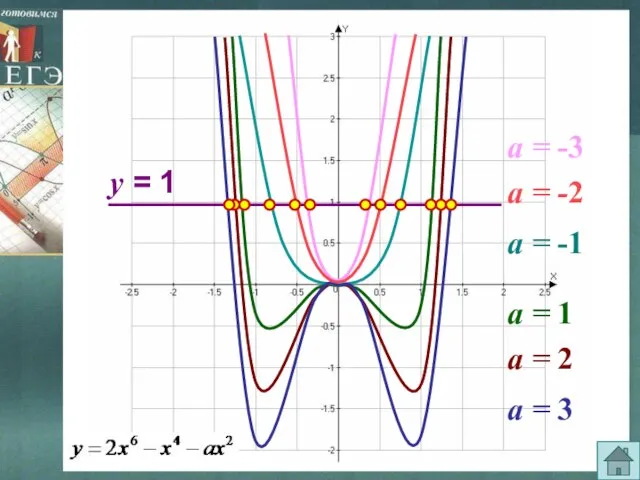
Пример. Может ли при каком-нибудь значении параметра а, уравнение иметь три корня?
ИСПОЛЬЗОВАНИЕ ЧЕТНОСТИ ФУНКЦИИ
Так как число 0 не является корнем уравнения, то уравнение имеет четное число корней.
Ответ: не может.
Графическая иллюстрация

а = 1
а = 2
а = 3
а = -3
а = -2
а = -1

Может ли при каком-нибудь значении параметра а, уравнение
Так как при замене х на –х данное уравнение не изменится, то множество его корней вместе с каждым корнем содержит противоположный корень. Следовательно, уравнение имеет четное число корней, отличных от нуля. Проверка показывает, что 0 – корень, значит, данное уравнение имеет нечетное число корней.
иметь нечетное число корней?
Решение.
Ответ: да.
ИСПОЛЬЗОВАНИЕ ЧЕТНОСТИ ФУНКЦИИ