Квадратные неравенства

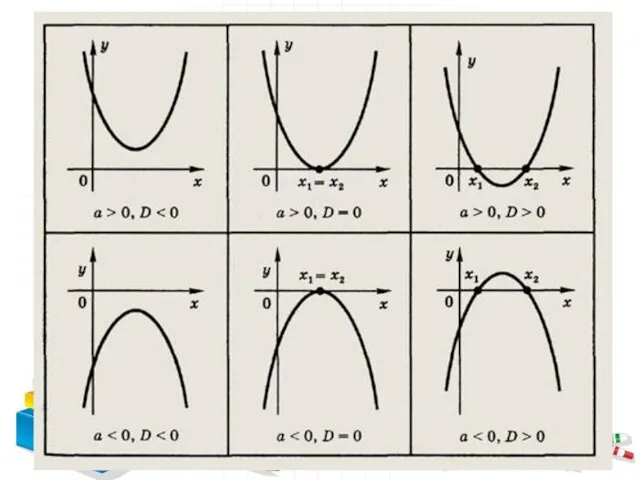
Инструкционная карта
Решение квадратных неравенств
ах2 + bx + с > 0 (< 0, ≥ 0, ≤ 0)
1. Вводим соответствующую функцию
у = ах2 + bx + с - квадратичная функция.
2. Определяем направление ветвей
параболы у = ах2 + bx + с ( при а > 0 ветви
направлены вверх; при а < 0 ветви
направлены вниз).
3. Находим нули функции, т.е. решаем
уравнение ах2 + bx + с =о.

4. Если уравнение имеет корни, то отмечаем
корни на координатной прямой и
схематически рисуем параболу в соответствии
с направлением ветвей. Если уравнение не
имеет корней, то схематически рисуем
параболу в соответствии с направлением
ветвей.
5. Находим решение неравенства с учетом
смысла знака неравенства.

Пример 1 D > 0
Решить неравенство -х2 - 2x + 3 ≥ 0.

Пример 1 D > 0
Решить неравенство -х2 - 2x + 3 ≥ 0.
Вводим функцию у = -х2 - 2x + 3 – квадратичная функция
а = -1 < 0, ветви
-х2 - 2x + 3 = 0
х = 1 и х = -3.
4. Отметим числа 1 и -3 на координатной
прямой и построим эскиз графика.

5. Т.к. знак неравенства (≥), то решением
является отрезок [-3; 1].
Ответ: [-3; 1].
-3
у
х
1

Пример 2 D = 0
Решить неравенство 4х2 + 4x + 1 > 0.

Пример 2 D = 0
Решить неравенство 4х2 + 4x + 1 > 0.
Вводим функцию f(x) = 4х2 + 4x + 1 - квадратичная функция .
а = 4 > 0 , ветви направлены вверх.
Решим уравнение 4х2 + 4x + 1 = 0
х1 = х2 = -0,5.
4. Парабола касается оси абсцисс.

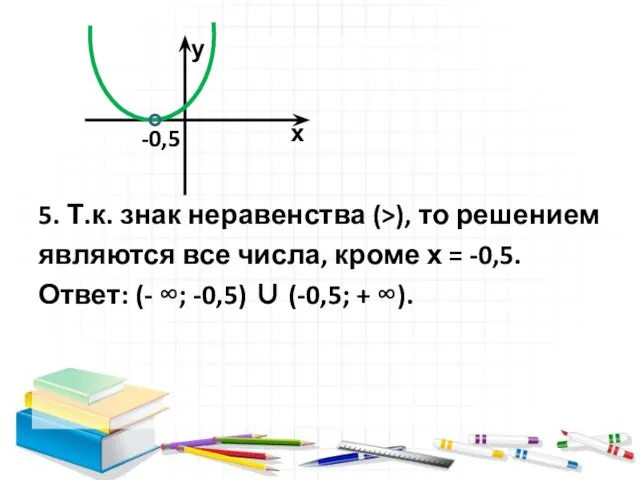
5. Т.к. знак неравенства (>), то решением
являются все числа, кроме х = -0,5.
Ответ: (- ∞; -0,5) ∪ (-0,5; + ∞).
-0,5
у
х

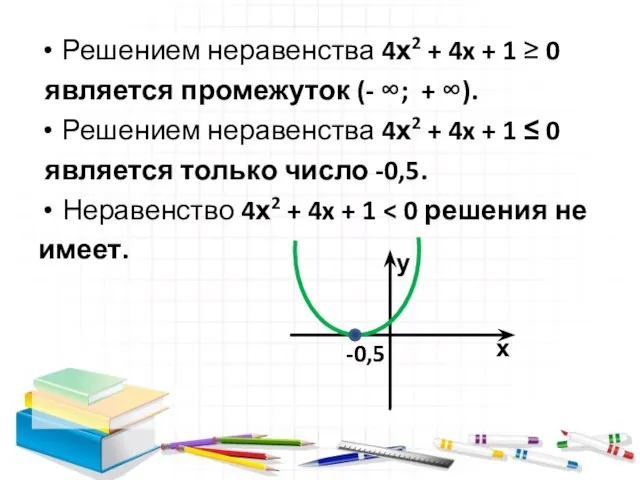
Решением неравенства 4х2 + 4x + 1 ≥ 0
является промежуток (- ∞; + ∞).
Решением неравенства 4х2 + 4x + 1 ≤ 0
является только число -0,5.
Неравенство 4х2 + 4x + 1 < 0 решения не
имеет.
-0,5
у
х

Пример 3 D < 0
Решить неравенство -х2 - 6x - 10 < 0.

Пример 3 D < 0
Решить неравенство -х2 - 6x - 10 < 0.
Вводим функцию f(x) = -х2 - 6x – 10 - квадратичная функция.
а = -1 < 0, ветви направлены вниз.
Уравнение -х2 - 6x - 10 = 0 решения не
имеет.
4. Парабола не пересекает ось х и не
касается её.

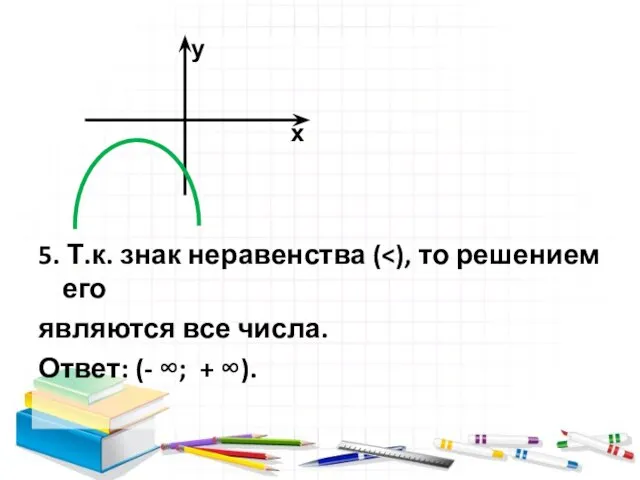
5. Т.к. знак неравенства (<), то решением его
являются все числа.
Ответ: (- ∞; + ∞).
у
х