Содержание
- 2. Введение Цель работы: 1. Совершенствовать уровень своей математической подготовки. 2. Овладеть некоторыми вопросами математического анализа. Задачи
- 3. Предел переменной величины Пределом переменной величины х называется постоянное число а, если для каждого наперед заданного
- 4. Рассмотрим несколько примеров переменных, стремящихся к пределу. Пример 1. Доказать, что переменная хn=1+ имеет предел, равный
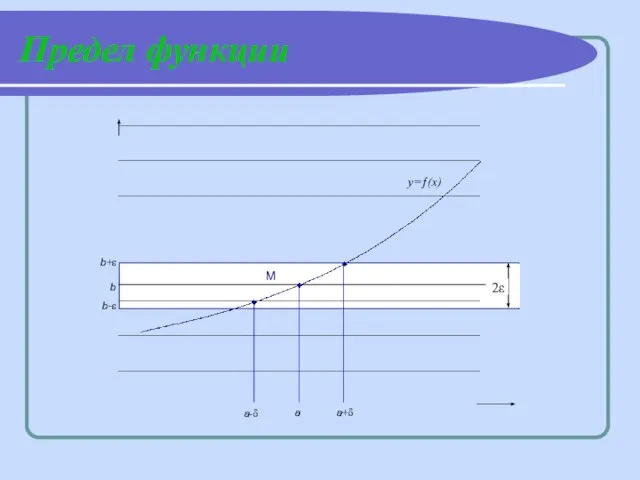
- 5. Предел функции Пределом функции ƒ(х) при х→а называется число b, если для любого положительного ε можно
- 6. Предел функции
- 7. Основные свойства пределов Свойство 1. Предел суммы нескольких переменных равен сумме пределов этих переменных: lim(a1+a2+…+an)= lim
- 8. Основные свойства пределов Первый замечательный предел: Второй замечательный предел: Далее я решил привести некоторые часто встречающиеся
- 9. Основные свойства пределов 3. 4.
- 10. Основные свойства пределов 5. 6. Пусть и=2+а, а→0.
- 11. Непрерывность функций Функция называется непрерывной в точке х0, если она определена в некоторой окрестности этой точки
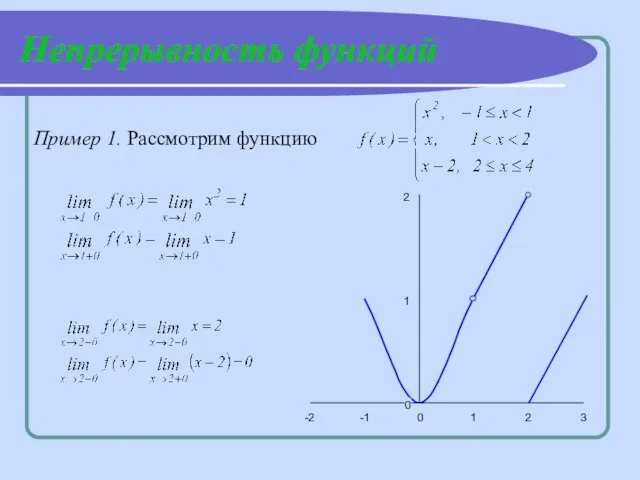
- 12. Непрерывность функций Пример 1. Рассмотрим функцию
- 14. Скачать презентацию









 Действие с дробями. Устная работа
Действие с дробями. Устная работа Тест 3 по математике
Тест 3 по математике Элементы нелинейного функционального анализа. Глава 1. Дифференциальное исчисление в нормированных пространствах
Элементы нелинейного функционального анализа. Глава 1. Дифференциальное исчисление в нормированных пространствах Сфера и плоскость
Сфера и плоскость Диаграммы
Диаграммы Решение составных задач
Решение составных задач Пирамида Кукулькана – величайший храм майя
Пирамида Кукулькана – величайший храм майя Текстовые задачи на движение по прямой
Текстовые задачи на движение по прямой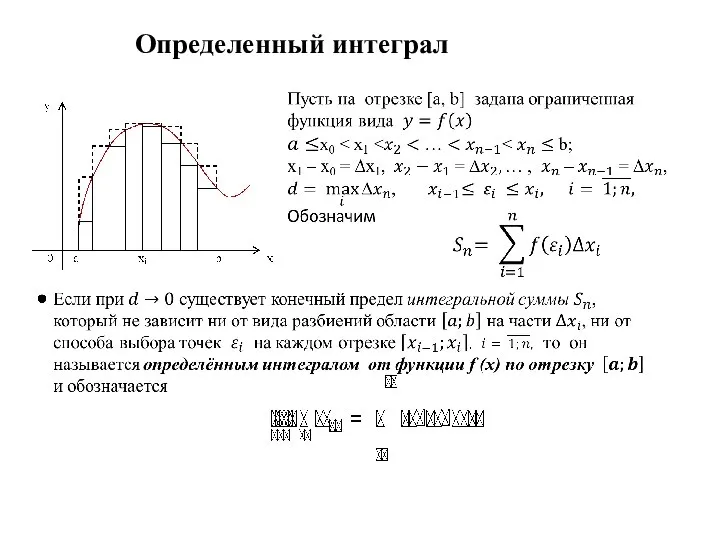 Определённый интеграл
Определённый интеграл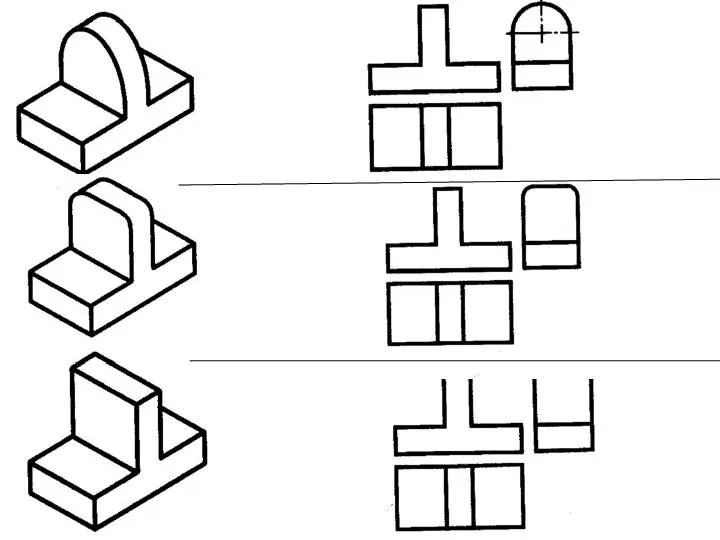 Проецирование на три взаимно перпендикулярные плоскости проекций
Проецирование на три взаимно перпендикулярные плоскости проекций Угол между прямыми
Угол между прямыми Porządki kompozycji symetria i asymetria
Porządki kompozycji symetria i asymetria Производная в экономике
Производная в экономике Цилиндр. Круговой цилиндр
Цилиндр. Круговой цилиндр Симметрия относительно прямой
Симметрия относительно прямой Презентация на тему Конусы в нашей жизни
Презентация на тему Конусы в нашей жизни  Математика в профессии геодезиста
Математика в профессии геодезиста Дидактический материал. Проверочные работы. Начальные понятия геометрии
Дидактический материал. Проверочные работы. Начальные понятия геометрии Аксиомы стереометрии
Аксиомы стереометрии Сумма углов треугольника
Сумма углов треугольника Определенный интеграл
Определенный интеграл Приближенные решения уравнений
Приближенные решения уравнений Определитель матрицы. Правило Крамера
Определитель матрицы. Правило Крамера Аналитическая панель
Аналитическая панель Презентация на тему АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ ПРОИЗВОЛЬНЫХ СТЕПЕНЕЙ
Презентация на тему АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ ПРОИЗВОЛЬНЫХ СТЕПЕНЕЙ 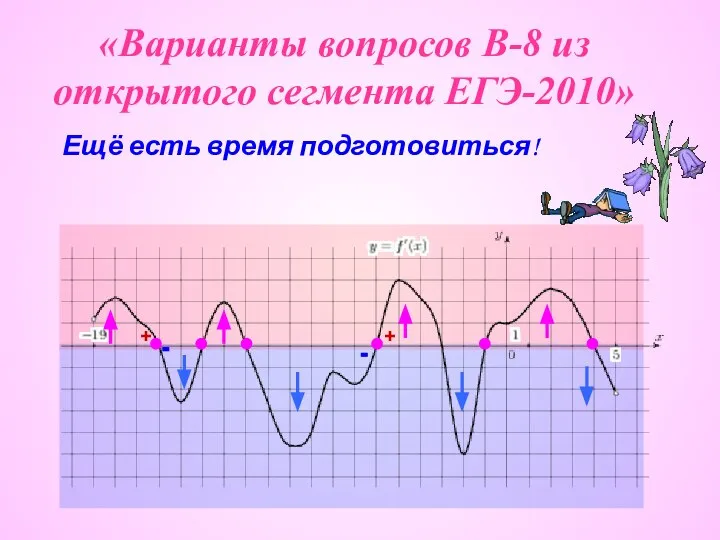 Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Прогрессии в окружающей нас жизни
Прогрессии в окружающей нас жизни Подготовка к ЕГЭ В-4. Курс лекций по математике
Подготовка к ЕГЭ В-4. Курс лекций по математике