Презентация на тему Звездчатые многогранники

Звёздчатый многогранник (звёздчатое тело) — это невыпуклый многогранник, грани которого пересекаются между собой. Как и у незвёздчатых многогранников грани попарно соединяются в ребрах, при этом внутренние линии пересечения не считаются рёбрами.
Звёздчатой формой многогранника называется многогранник, полученный путём продления граней данного многогранника через рёбра до их следующего пересечения с другими гранями по новым рёбрам.
Гравюра Эшера Мориса

Правильные звёздчатые многогранники - это звёздчатые многогранники, гранями которых являются одинаковые правильные или звёздчатые многоугольники. Коши установил, что существует всего 4 правильных звёздчатых тела, не являющиеся соединениями платоновых и звёздчатых тел, называемые телами Кепплера-Пуансо: все 3 звёздчатых формы додекаэдра и одна из звёздчатых форм икосаэдра. Остальные правильные звёздчатые многогранники являются или соединениями платоновых тел, или соединениями тел Кепплера-Пуансо.

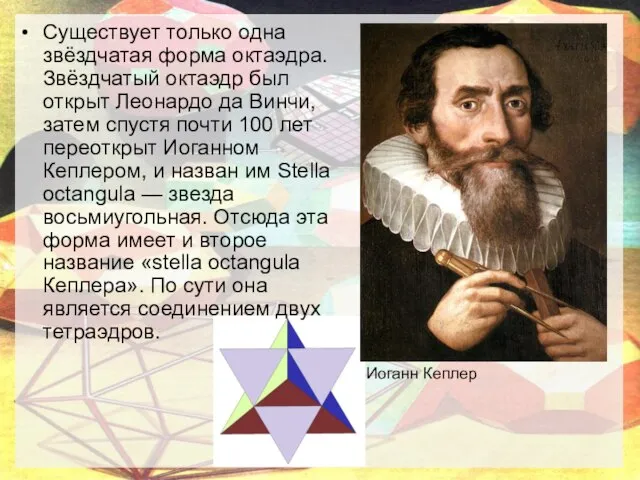
Существует только одна звёздчатая форма октаэдра. Звёздчатый октаэдр был открыт Леонардо да Винчи, затем спустя почти 100 лет переоткрыт Иоганном Кеплером, и назван им Stella octangula — звезда восьмиугольная. Отсюда эта форма имеет и второе название «stella octangula Кеплера». По сути она является соединением двух тетраэдров.
Иоганн Кеплер

Додекаэдр имеет 3 звёздчатые формы: малый звёздчатый додекаэдр, большой додекаэдр, большой звёздчатый додекаэдр (звёздчатый большой додекаэдр, завершающая форма). Первые две из них были открыты Кеплером (1619), третья — Пуансо (1809). В отличие от октаэдра любая из звёздчатых форм додекаэдра не является соединением платоновых тел, а образует новый многогранник.
Все 3 звёздчатые формы додекаэдра, вместе с большим икосаэдром образуют семейство тел Кеплера-Пуансо, то есть правильных невыпуклых (звёздчатых) многогранников.
У большого додекаэдра гранями являются пятиугольники, которые, сходятся по пять в каждой из вершин. У малого звёздчатого и большого звёздчатого додекаэдров грани - пятиконечные звёзды (пентаграммы), которые в первом случае сходятся по 5, а во втором по 3.
малый звёздчатый додекаэдр большой додэкаэдр большой звездчатый додэкаэдр

В работе "О многоугольниках и многогранниках" (1810) Пуансо описал четыре правильных звездчатых многогранника, но вопрос о существовании других таких многогранников оставался открытым. Ответ на него был дан год спустя, в 1811 году, французским математиком О. Коши. В работе «Исследование о многогранниках» он доказал, что других правильных звездчатых многогранников не существует.
О.Коши
Луи Пуансо

Кроме правильных звездчатых многогранников существуют и другие звездчатые формы, получающиеся продолжением граней правильных и полуправильных многогранников.
Продолжения граней кубооктаэдра приводят к четырем звездчатым многогранникам. Они представлены на рисунке 21.

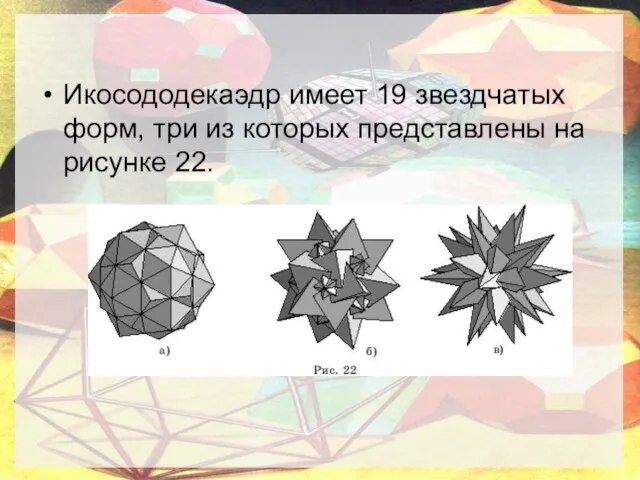
Икосододекаэдр имеет 19 звездчатых форм, три из которых представлены на рисунке 22.

Наконец, икосаэдр имеет 59 звездчатых форм, три из которых представлены на рисунке 23.

Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений. Применяются они и в архитектуре.
Многие формы звездчатых многогранников подсказывает сама природа в виде кристаллов. Снежинки - это тоже звездчатые многогранники. С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок.

Модель большого додекаэдра использовали в качестве памятника к одной из годовщин Победы. Установлена она на питерском проспекте Науки (недалеко от метро "Академическая").

Ниже показана мраморная инкрустация, которая изображает небольшой звездчатый додекаэдр, расположенных в полу базилики святого Марка в Венеции. Предположительно она была создана итальянским художником XIV века Пауло Учелло еще в 1420 году. Если это действительно так то открытие многогранника произошло за двести лет до математического описания этого же многогранник в 1619 Кеплером.

Открыв малый звездчатый додэкаэдр, Кеплер назвал его «еж» и поместил в свою удивительную по фантастичности идей книгу «Мировая гармония» Но ученые отказывались считать кеплеровского ежа многогранником.
У этого упрямства была своя логика и своя предыстория. Столетиями математики не признавали за всякого рода звездами права называться многоугольниками из-за того, что стороны их пересекаются.
А тут — геометрическое тело, гранями которого служат пятиконечные звезды, да еще вдобавок пересекающиеся! Довод был прост и весом: это кеплеровское животное не подчиняется формуле Эйлера: Высоты + Грани – Ребра = 2. Конечно же, геометрический ежик не настолько уж колюч, чтобы восстать против непогрешимой формулы. Надо только взглянуть на него как на простое, честное геометрическое тело, составленное из 60 треугольников, имеющее 90 ребер и 32 вершины. Тогда В + Г - Р = 32 + 60 – 90 = 2 как и положено.
Кеплер не додумался, что у полученной им фигуры есть двойник. Это увидел Август Фердинад Мебиус, а сам многогранник — «большой додекаэдр» — построил французский геометр Луи Пуансо, спустя без малого двести лет после кеплеровских звездчатых фигур.

Рисуя правильные многогранники в книге Луки Пачоли «О божественной пропорции», Леонардо да Винчи не пользовался циркулем и линейкой. По его записям также видно, что он мало вычислял. Практически нет никаких сомнений, что он рисовал многогранники со сделанных его руками моделей. Лука Пачоли обращает внимание на перспективное представление 60 сделанных им рисунков, что также свидетельствует о большой предварительной работе, проделанной им по изготовлению этих моделей.
В связи с затронутой нами темой Брагина пишет: «Здесь он [Лука Пачоли] вновь воздает хвалу рисункам Леонардо, сделанным для его книги "О божественной пропорции". Леонардо создал прекрасные фигуры многогранников — "высочайшего [уровня] легчайшие [изящные] фигуры всех платоновских и математических тел, как правильных, так и производных [от правильных], рисунки которых выполнил в изометрической перспективе столь совершенно, что лучше сделать было бы невозможно…".
Звездчатый октаэдр
Малый звездчатый додекаэдр

Гравюры Эшера Мориса
Хаос и порядок
Тяготение
Двойная планета