Презентация по математике "Алгоритмы внутренних точек с приближенным решением вспомогательной задачи" -
Содержание
- 2. 1939 – линейное программирование (Канторович). 1947 – симплекс-метод (Данциг). 1967 – метод внутренних точек (Дикин). 1984
- 3. Основные классы алгоритмов внутренних точек (1) (2) Пара взаимно-двойственных задач линейного программирования Аффинно-масштабирующие алгоритмы. Алгоритмы центрального
- 4. Аффинно-масштабирующие алгоритмы внутренних точек Стартовое приближение: Итеративный переход: Задача поиска направления корректировки: Шаг корректировки: (3) Способы
- 5. Алгоритмы центрального пути (имеют полиномиальные оценки) Логарифмическая барьерная функция: (8) Задача поиска направления корректировки: Комбинированные алгоритмы
- 6. Решение вспомогательной задачи Аффинно-масштабирующие алгоритмы: Алгоритмы центрального пути: Комбинированные алгоритмы: (11) (12) (13) (14) (17) (18)
- 7. Методы решения вспомогательной задачи Метод Гаусса. Метод Халецкого (метод квадратного корня). Метод сопряженных направлений. Метод Зейделя.
- 8. Метод сопряженных направлений Направление корректировки: Шаг, определяющий вариант метода: Итеративный переход: Шаг корректировки:
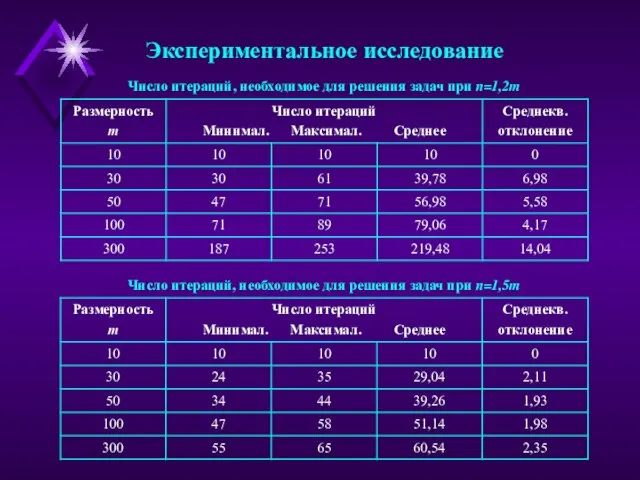
- 9. Экспериментальное исследование Число итераций, необходимое для решения задач при n=1,2m Число итераций, необходимое для решения задач
- 10. Параметры управления алгоритмом Вариант приближенного метода. ε – параметр в условии останова δ – параметр в
- 12. Скачать презентацию








 Площадь треугольника
Площадь треугольника Первый признак равенства треугольников
Первый признак равенства треугольников Алгебраический способ решения задач (часть 1)
Алгебраический способ решения задач (часть 1) Солнечная система. Обыкновенные дроби
Солнечная система. Обыкновенные дроби Модели скоростей при движении по реке. 5 класс
Модели скоростей при движении по реке. 5 класс Дробь. Подготовка к олимпиадам
Дробь. Подготовка к олимпиадам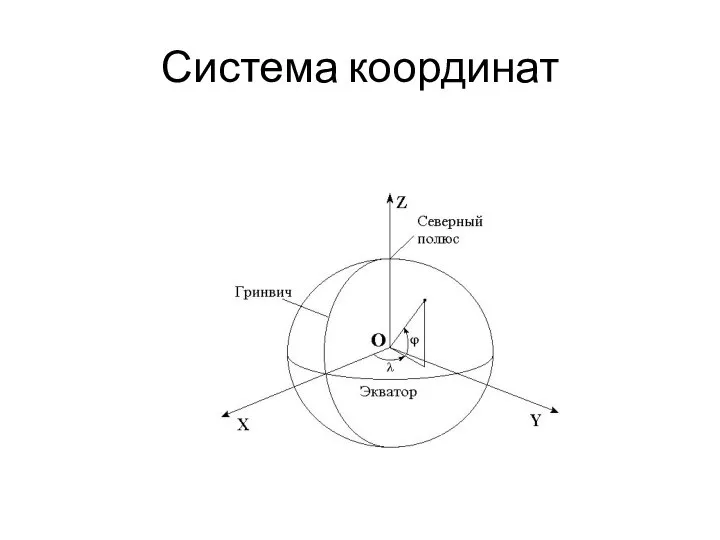 Система координат. Географические координаты
Система координат. Географические координаты Измерение углов, расстояний. Теодолит, устройство, поверки (лекция 5)
Измерение углов, расстояний. Теодолит, устройство, поверки (лекция 5) Ряды. Лекция
Ряды. Лекция Урок математики 9 класс учитель Курохтина В.А. МОУ СОШ № 1 г. Пыть-Ях
Урок математики 9 класс учитель Курохтина В.А. МОУ СОШ № 1 г. Пыть-Ях Геометрическая прогрессия
Геометрическая прогрессия Деление обыкновенных дробей. 5 класс
Деление обыкновенных дробей. 5 класс Первое знакомство с понятием вероятности. 6 класс
Первое знакомство с понятием вероятности. 6 класс Задачи на проценты
Задачи на проценты Задания по математике
Задания по математике Составление фигур из спичек
Составление фигур из спичек Задачи. Итоговое повторение
Задачи. Итоговое повторение Роль дисплазии соединительной ткани в формировании остеопенического синдрома у детей
Роль дисплазии соединительной ткани в формировании остеопенического синдрома у детей Аналитическая геометрия
Аналитическая геометрия Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)
Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша) Математика. Прогулка в осенний лес. 2 класс
Математика. Прогулка в осенний лес. 2 класс Задачи по геометрии
Задачи по геометрии Производная сложной функции
Производная сложной функции Метод наименьших квадратов. Ordinary Least Squares, OLS
Метод наименьших квадратов. Ordinary Least Squares, OLS Линейная алгебра
Линейная алгебра Двойные интегралы
Двойные интегралы Приключение олобка на тропинке умножения. Тренажер
Приключение олобка на тропинке умножения. Тренажер Тест на распознавание предметов
Тест на распознавание предметов