Презентация по математике "Числовые неравенства" -

Самостоятельная работа
Вариант 1
Дайте определение, что число a больше числа b
Сравните: а) б) а2 + 16 и 8а
Докажите неравенство (а – 3)(а + 9 ) < (а+3)(а + 5)
Вариант 2
Дайте определение, что число a меньше числа b
Сравните: а) б) а2 + 25 и 10а
Докажите неравенство (а – 2)(а + 9 ) < (а+3)(а + 4)

Теорема 1 Если а>b, то b
Если а
a
Теорема 2 Если а
Теорема 3 Если а < b и c – любое число, то a + с < b + c
Теорема 4 Если а < b и c – положительное число, то a * с < b * c
Если а < b и c – отрицательное число, то a * с > b * c

Если a и b положительные числа и a < b, то
Пример 1
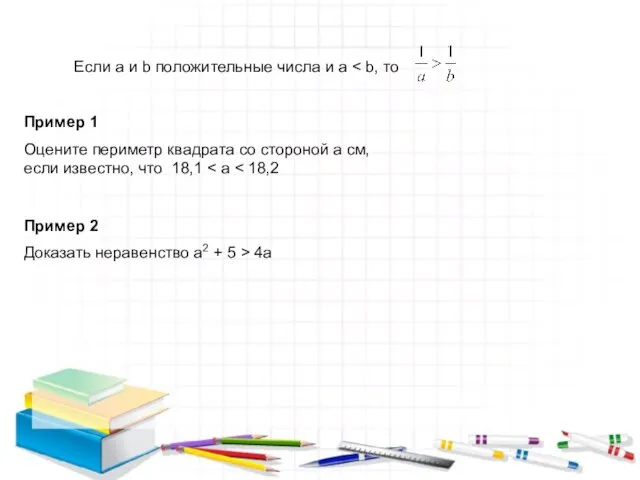
Оцените периметр квадрата со стороной a см, если известно, что 18,1 < a < 18,2
Пример 2
Доказать неравенство a2 + 5 > 4a

В классе №748 № 731 № 749(г) №750 - № 754 (в,г)
д/з п29 №749 - № 754 (а,б)

1. Если a > b и b > c , то a > c.
Например, 6 > 4 и 4 > -1, тогда 6 > -1.
Аналогично, если c < b и b < a , то c < a.
2. Если a > b, то a + c > b + c.
Если к обеим частям неравенства прибавить одно и то же число
(положительное или отрицательное), то знак неравенства не
изменится.
Например, 6 > 4, тогда 6 + 3 > 4 + 3.
3. Если a + c > b, то a > b - c.
Любое слагаемое можно переносить из одной части неравенства
в другую, изменяя при этом знак слагаемого на противоположный.
Например, 5 + 10 > 4, тогда 5 > 4 – 10.

a b
4. Если a > b и c > 0 , то ac > bc и .
c c
Если обе части неравенства умножить или разделить на одно и
то же положительное число, то знак неравенства не изменится.
Например, 3 > 1, тогда 3 ∙ 5 > 1 ∙ 5.
7 < 21, тогда 7 : 7 < 21 : 7.
a b
Если a > b и c < 0, то ac < bc и .
c c
Если обе части неравенства умножить или разделить на одно и
то же отрицательное число, то знак неравенства изменится на
противоположный.
Например, 9 > 4, тогда 9 ∙ (-2) < 4 ∙ (-2).
12 < 30, тогда 12 : (-3) > 30 : (-3).

5. Если a > b и c > d, то a + c > b + d.
При сложении неравенств одинакового знака получается
неравенство того же знака.
Например, 8 > 5 и 4 > 1, тогда 8 + 4 > 5 + 1.
6. Если для положительных чисел a, b, c, d: a > b и c > d, то
a ∙ c > b ∙ d.
При умножении неравенств одинакового знака, у которых левые и
правые части положительны, получается неравенство того же
знака.
Например, 12 > 5 и 3 > 2, тогда 12 ∙ 3 > 5 ∙ 2.