Презентация по математике "Перевод из десятичной системы счисления в другую систему счисления и обратно" -

Перевод из десятичной системы счисления в другую систему счисления и обратно.
Перевод целых чисел
Перевод дробных чисел
Перевод смешанных чисел
Перевод в десятичную систему счисления
В

Перевод из десятичной системы счисления в другую систему счисления и обратно.
При переводе целых чисел из десятичной системы в любую другую систему, необходимо:
Десятичное число последовательно делить на основание другой системы, до тех пор пока частное не окажется меньше основания.
Запись получившегося числа осуществляется справа налево.
Цифрами числа будут являться остатки от деления, начиная с последнего частного.
В
Н

Пример 1. Перевести число 63 в двоичную систему счисления.
63
2
31
62
1
2
-
-
30
1
15
2
7
-
14
1
2
-
6
1
3
2
-
2
1
1
а0=
а1=
а2=
а3=
а4=
= а5
Для обозначения цифр в записи числа используем символику: а0, а1, а2, а3, а4, а5.
Отсюда: 6310 = 1111112 (а5 а4 а3 а2 а1 а0)
В
Н

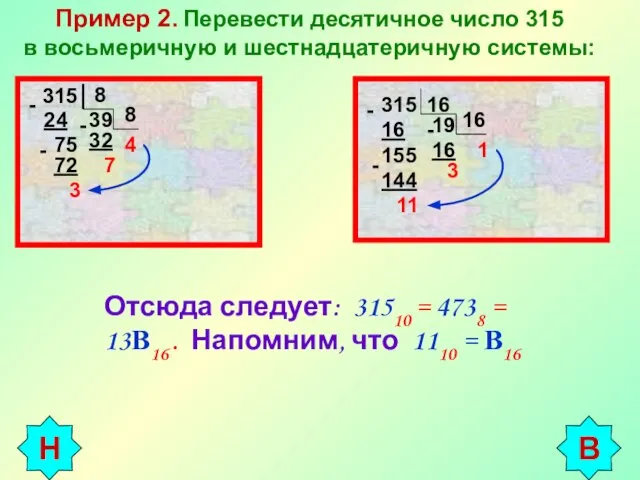
Пример 2. Перевести десятичное число 315
в восьмеричную и шестнадцатеричную системы:
315
8
-
24
75
-
72
3
39
8
-
32
7
4
315
16
-
16
155
-
144
11
19
16
-
16
3
1
Отсюда следует: 31510 = 4738 = 13В16 . Напомним, что 1110 = В16
В
Н

Перевод из десятичной системы счисления в другую систему счисления и обратно.
При переводе дробных чисел из десятичной системы в любую другую систему, необходимо:
Последовательно умножать данное число на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления.
Запись получившегося числа осуществляется сверху вниз.
Цифрами числа будут являться полученные целые части произведений.
В
Н

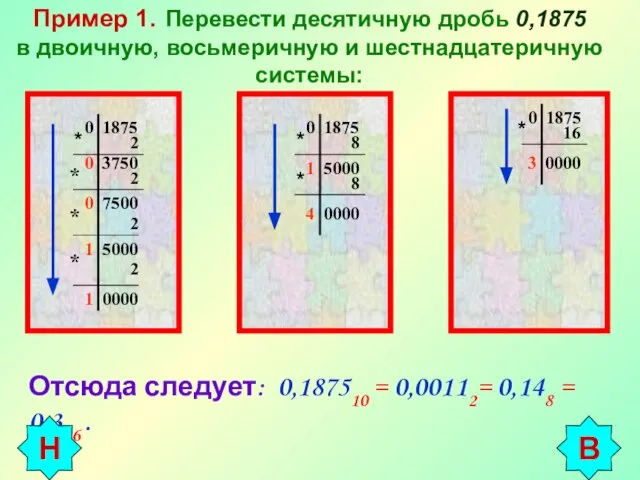
Пример 1. Перевести десятичную дробь 0,1875
в двоичную, восьмеричную и шестнадцатеричную системы:
0 1875
*
2
0 3750
*
2
0 7500
*
2
1 5000
2
*
1 0000
0 1875
*
8
1 5000
*
8
4 0000
0 1875
*
16
3 0000
Отсюда следует: 0,187510 = 0,00112= 0,148 = 0,316 .
В
Н

Перевод из десятичной системы счисления в другую систему счисления и обратно.
Перевод смешанных чисел, содержащих целую и дробную части из десятичной системы в любую другую систему осуществляется в два этапа. Целая и дробная части исходного числа переводятся отдельно по соответствующим алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой (точкой).
Пример1. Перевести десятичное число 315.187510 в восьмеричную и в шестнадцатеричную системы счисления.
Из рассмотренных выше примеров следует:
315.187510 = 473.148 = 13В.316.
В
Н

Перевод из десятичной системы счисления в любую другую систему счисления и обратно.
Обратное преобразование чисел из любой системы счисления в десятичную систему осуществляется с помощью выражения вида:
ХS = A0S0 + A1S1 + A2S2 + …
где ХS – число в S-й системе счисления,
S – основание системы, А – цифра числа.
Данное выражение используется для преобразования целых чисел, причем отчет цифр идет справа налево.
В
Н