Слайд 2Большинство физических, химических, экономических и прочих процессов описываются дифференциальными уравнениями или системами

дифференциальных уравнений. Возникает необходимость получения результатов их решения. И не всегда есть возможность получить точный ответ аналитическим способом.
Поэтому требуются навыки в решении ДУ с использованием численных методов. Один из таких методов – метод ломаных Эйлера. Рассмотрим решение дифференциального уравнения усовершенствованным методом ломаных Эйлера, который имеет большую точность расчетов.
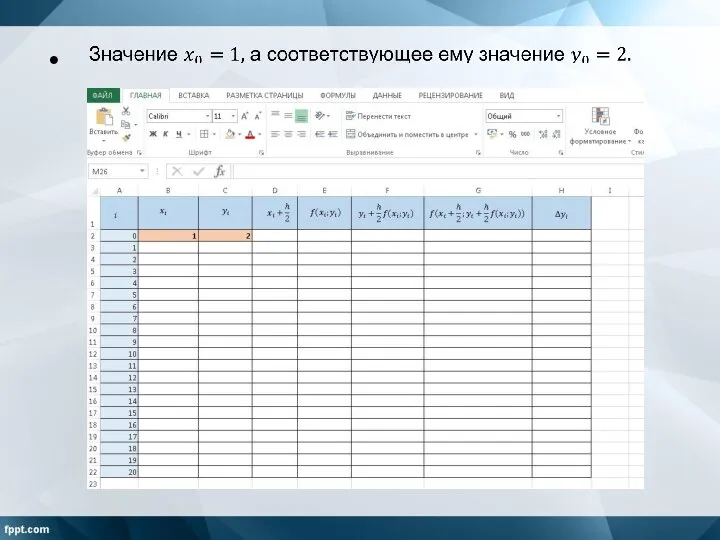
Слайд 4Даем название столбцам таблицы в соответствии с алгоритмом для решения ДУ аналитически.
Создание
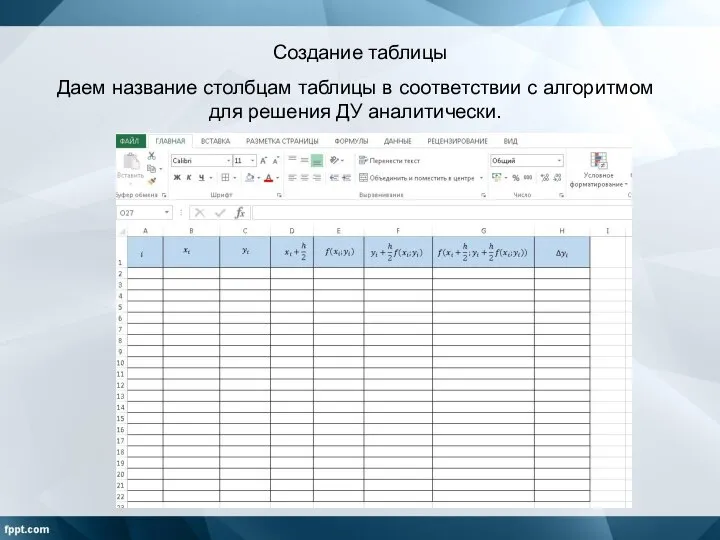
таблицы
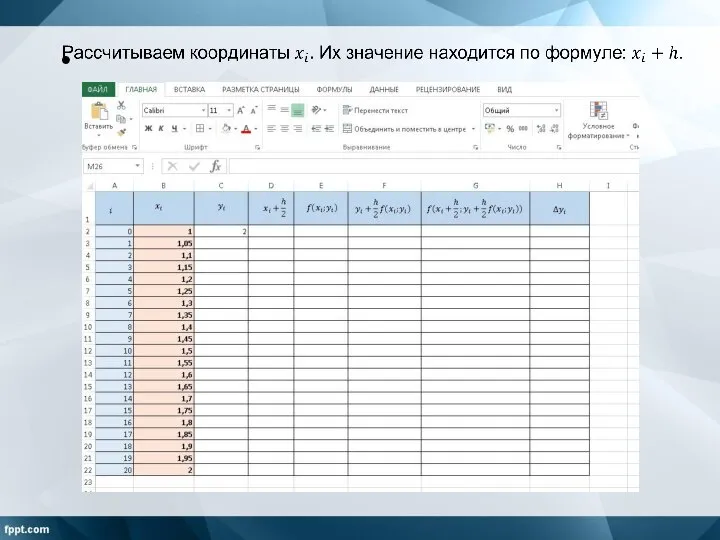
Слайд 5Длина отрезка равна единице, а шаг разбиения – 0,05. Количество узловых точек
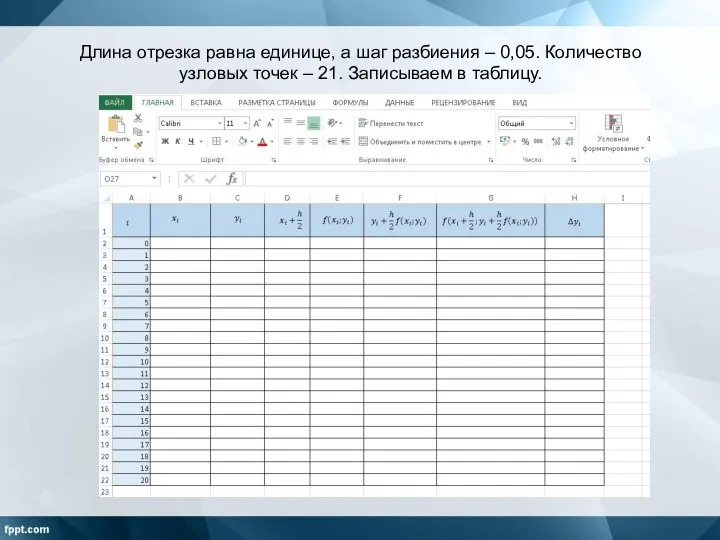
– 21. Записываем в таблицу.
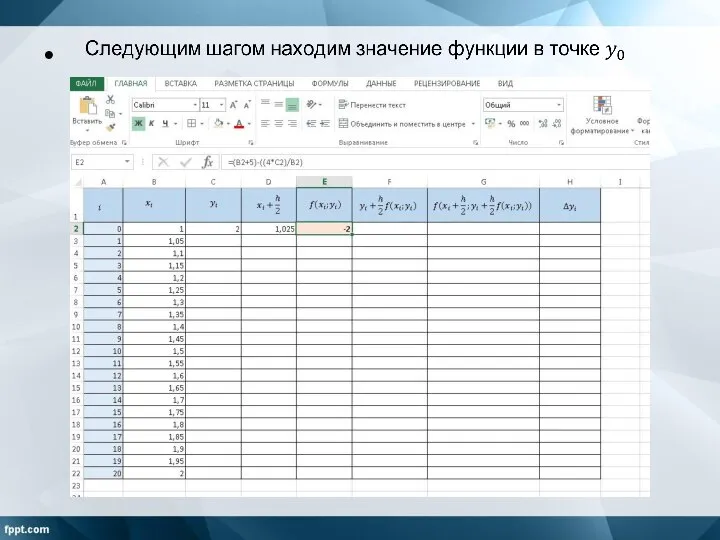
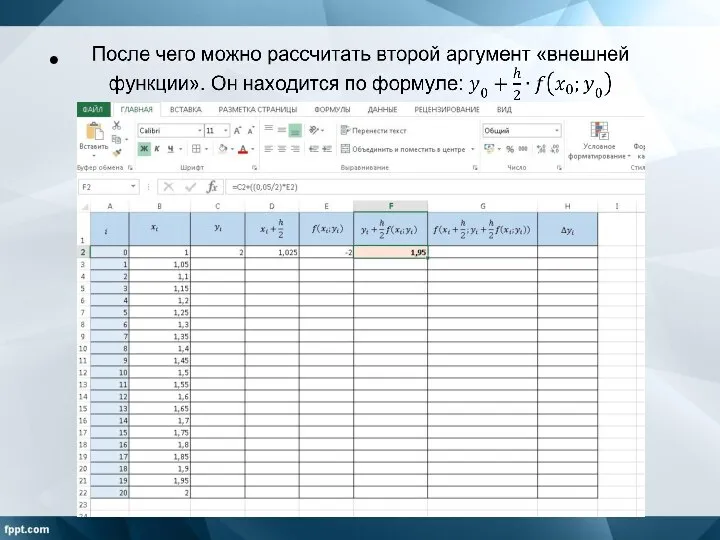
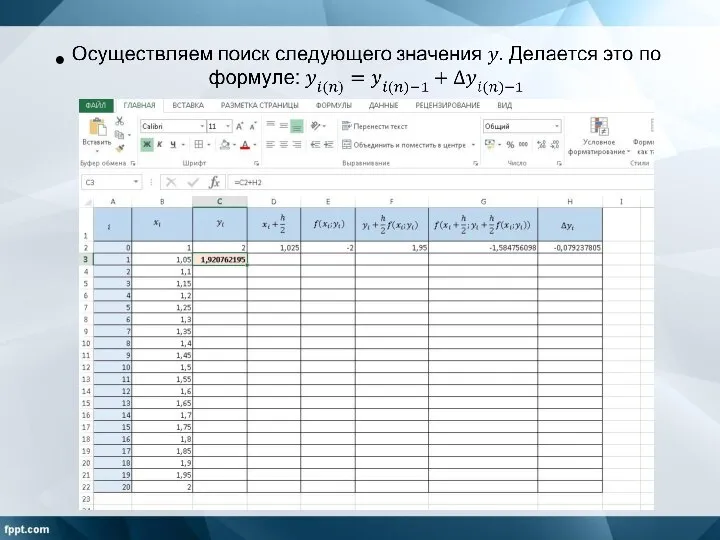
Слайд 8Находим первый аргумент «внешней функции».
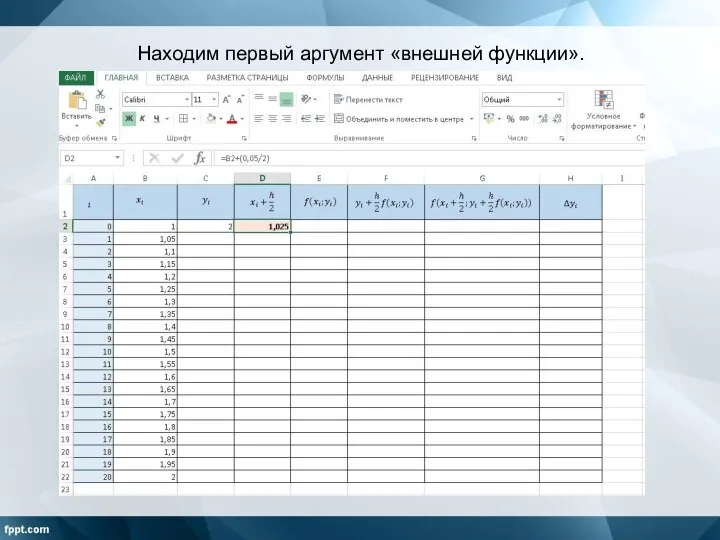
Слайд 11Ищем значение функции в точке, рассчитанной с учетом погрешности.
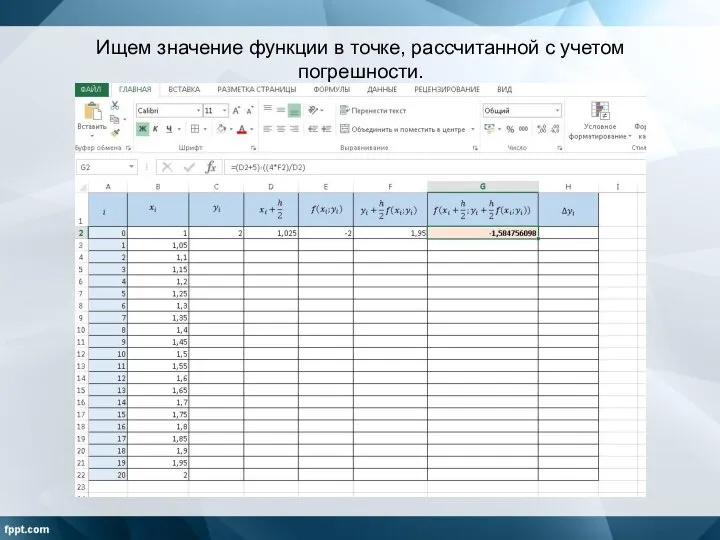
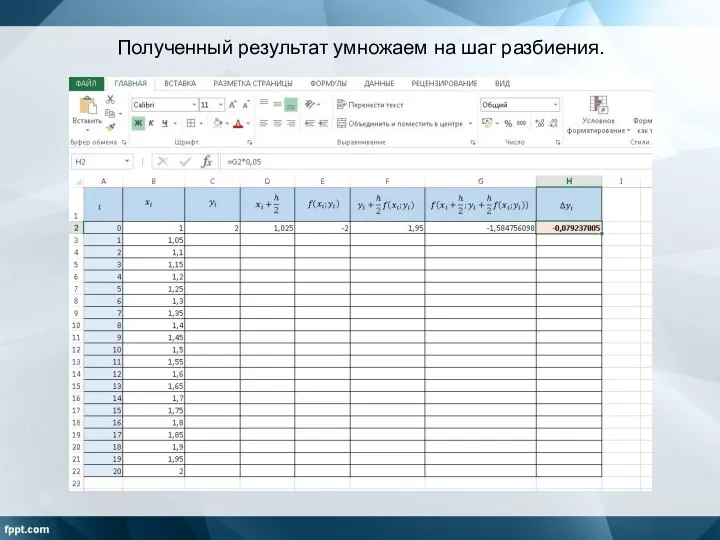
Слайд 12Полученный результат умножаем на шаг разбиения.
Слайд 14Копируем полученные значения по образцу. (Выделяем значения полей D, E, F, G,
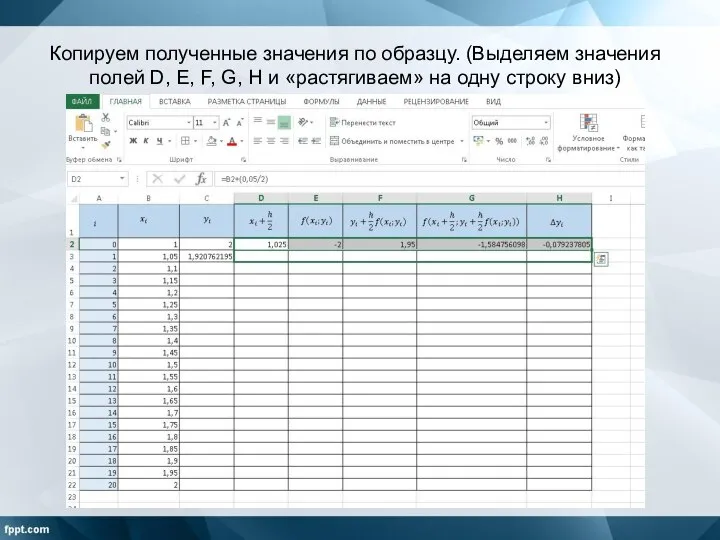
H и «растягиваем» на одну строку вниз)
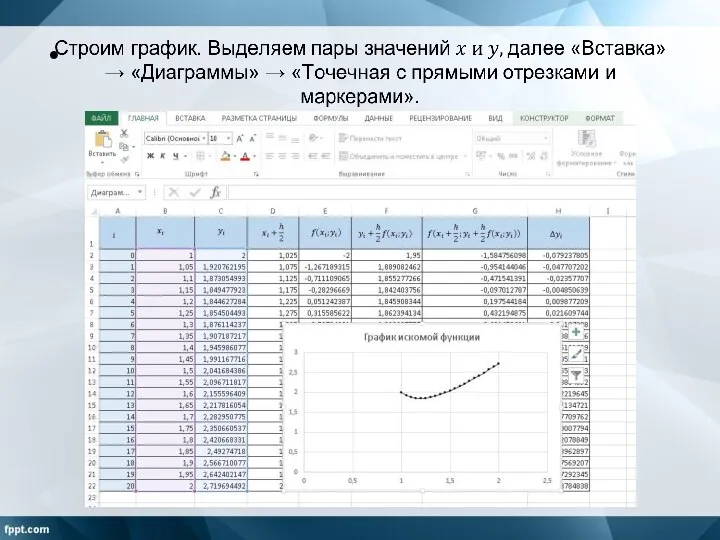
Слайд 15(Выделяем значения полей C, D, E, F, G, H и «растягиваем» до
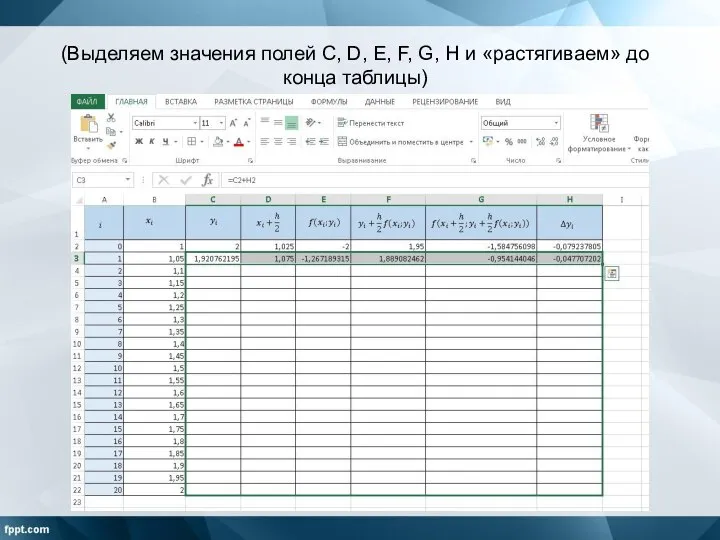
конца таблицы)
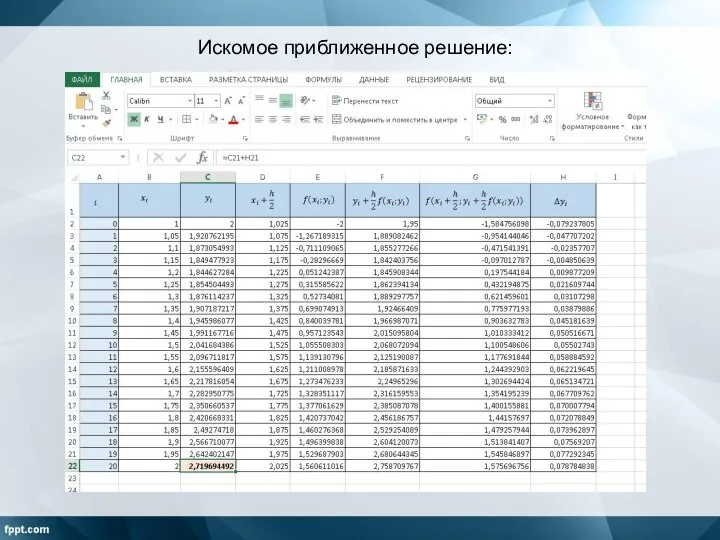
Слайд 18При решении данного ДУ аналитически результат будет равен ─ 2,71875.
Вывод: усовершенствованный метод

ломаных Эйлера дает более точные результаты в отличие от «классического» метода. Связано это с тем, что производная берется не в начале шага, а как промежуточное или среднее на разных участках одного шага. В процессе использования метода вычисляются несколько производных в разных частях шага, которые впоследствии усредняются. За счет этого точность метода возрастает на порядок.









 Системы и совокупности неравенств с одной переменной
Системы и совокупности неравенств с одной переменной Квадрат. Свойства и признаки квадрата
Квадрат. Свойства и признаки квадрата Тригонометрические функции
Тригонометрические функции Смежные и вертикальные углы
Смежные и вертикальные углы Признаки и свойства параллельных прямых
Признаки и свойства параллельных прямых Решение линейных неравенств с одной переменной. Числовые промежутки. Урок 15
Решение линейных неравенств с одной переменной. Числовые промежутки. Урок 15 Дифференциальное исчисление функции нескольких переменных
Дифференциальное исчисление функции нескольких переменных Решение задач на одновременное встречное движение
Решение задач на одновременное встречное движение Итерактивная мозаика
Итерактивная мозаика Презентация по математике "Дроби в Древнем Риме" -
Презентация по математике "Дроби в Древнем Риме" -  Отбор корней тригонометрического уравнения с помощью окружности
Отбор корней тригонометрического уравнения с помощью окружности Пространство и размерность
Пространство и размерность Розв'язання задач
Розв'язання задач Параллелограмм ауданы. 8сынып
Параллелограмм ауданы. 8сынып комбинаторика 1 лекция-1
комбинаторика 1 лекция-1 Метод линейного сплайна
Метод линейного сплайна Вычисление площадей фигур с помощью определенного интеграла
Вычисление площадей фигур с помощью определенного интеграла Неравенства. Тест
Неравенства. Тест Основное свойство дроби. Сокращение дробей
Основное свойство дроби. Сокращение дробей Теорема синусов
Теорема синусов Гипотеза Пуанкаре́
Гипотеза Пуанкаре́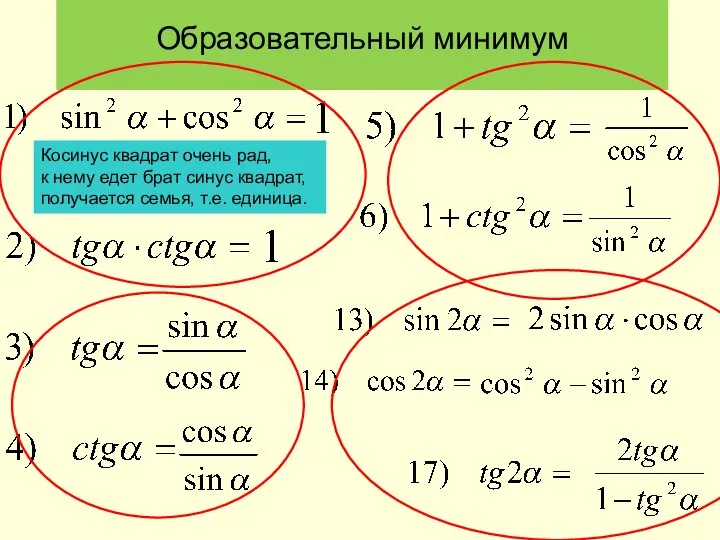 Образовательный минимум
Образовательный минимум Вычисление рациональным способом
Вычисление рациональным способом Взаимно-обратные задачи. 2 класс
Взаимно-обратные задачи. 2 класс Парная регрессия: линейный анализ
Парная регрессия: линейный анализ Отношения. Дискретная математика
Отношения. Дискретная математика Построение информационной модели метода изготовления изделия
Построение информационной модели метода изготовления изделия Расстояние от точки до прямой
Расстояние от точки до прямой