Содержание
- 2. 1. Историческая справка Впервые мнимые величины появились в работе Дж. Кардано «Великое искусство, или об алгебраических
- 3. Основные понятия Комплексным числом называется выражение вида z=a+bi , где a и b действительные числа, а
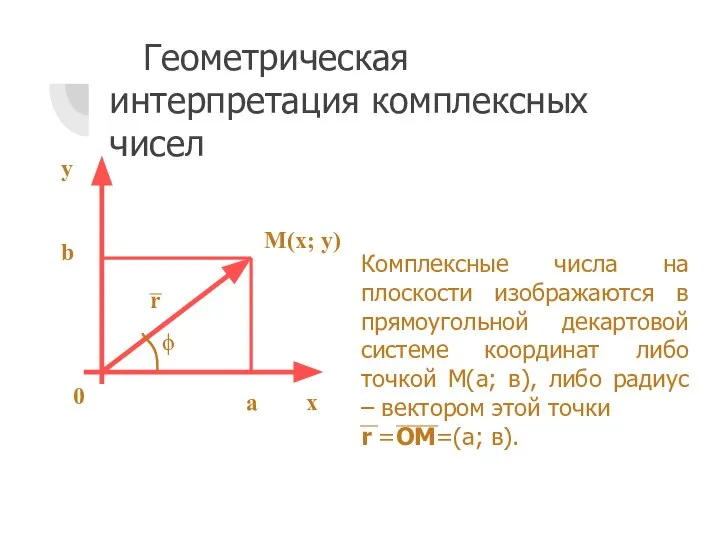
- 4. Геометрическая интерпретация комплексных чисел Комплексные числа на плоскости изображаются в прямоугольной декартовой системе координат либо точкой
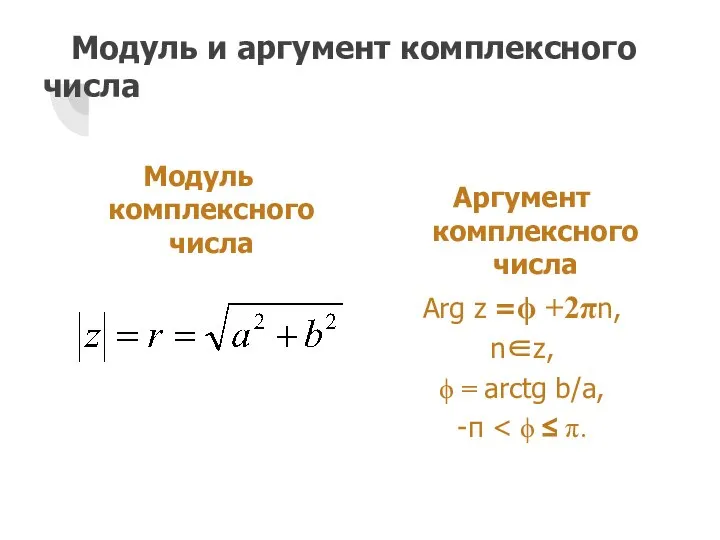
- 5. Модуль и аргумент комплексного числа Модуль комплексного числа Аргумент комплексного числа Arg z =ϕ +2πn, n∈z,
- 6. Найти модуль комплексного числа Вычислить По знакам и определить четверть, в которой заканчивается искомый угол Найти
- 7. 6. Формы записи комплексных чисел Алгебраическая z =a + bi Тригонометрическая z = r (cos φ
- 8. Комплексные числа в экономике Сегодня сложно представить себе ряд наук без применения комплексных чисел. Теория электротехники,
- 10. Скачать презентацию





 Комплексные числа и действия над ними
Комплексные числа и действия над ними Цена деления и предел измерения линейки
Цена деления и предел измерения линейки Состав чисел
Состав чисел Умножение десятичных дробей. Графический диктант
Умножение десятичных дробей. Графический диктант Властивості і графіки тригонометричних функцій. Графік тангенса та котангенса числового аргументу
Властивості і графіки тригонометричних функцій. Графік тангенса та котангенса числового аргументу Реши уравнения
Реши уравнения Числоа 6, 7. Письмо цифры 6
Числоа 6, 7. Письмо цифры 6 Треугольники
Треугольники Теорема Виета. Урок систематизации, обобщения и контроля знаний
Теорема Виета. Урок систематизации, обобщения и контроля знаний Презентация на тему Метод интервалов
Презентация на тему Метод интервалов  Решение уравнений с одной переменной
Решение уравнений с одной переменной Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений Признаки параллельности прямых
Признаки параллельности прямых Умножение и деление отрицательных чисел. Урок-путешествие
Умножение и деление отрицательных чисел. Урок-путешествие Преобразование графиков вида у=f(х±а)
Преобразование графиков вида у=f(х±а) Математика. Числа до 20
Математика. Числа до 20 Какой функции соответствует график
Какой функции соответствует график Контрольная работа
Контрольная работа Теория антагонистических игр. Задачи для выполнения
Теория антагонистических игр. Задачи для выполнения Интерактивный тренажёр Весёлый счёт. Математика 1 класс
Интерактивный тренажёр Весёлый счёт. Математика 1 класс Задачи на перебор вариантов
Задачи на перебор вариантов Решение тригонометрических уравнений
Решение тригонометрических уравнений Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Дифференциальные уравнения высшего порядка
Дифференциальные уравнения высшего порядка Итогово-обобщающий урок. Площадь. Теорема Пифагора
Итогово-обобщающий урок. Площадь. Теорема Пифагора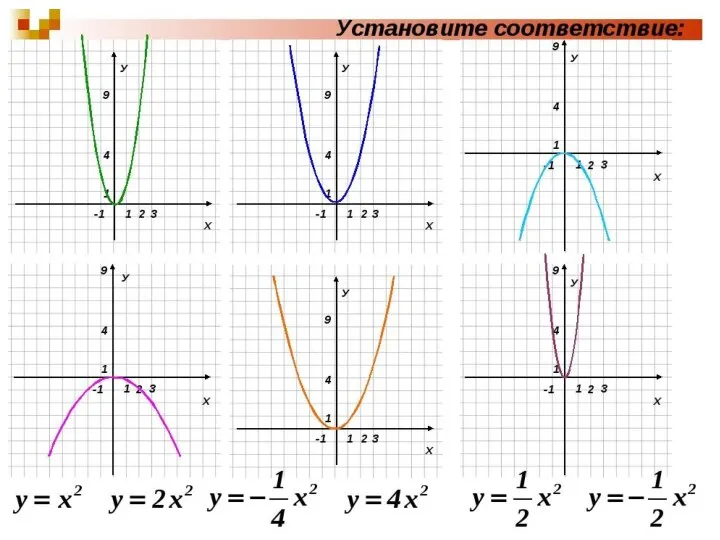 Графики функций
Графики функций Результант. Литература
Результант. Литература Занятие 45. Формулы двойного угла. Формулы половинного угла
Занятие 45. Формулы двойного угла. Формулы половинного угла