Призма, её элементы

Определение призмы:
А1А2…АnВ1В2Вn– призма
Многоугольники А1А2…Аn и В1В2…Вn – основания призмы
Параллелограммы А1А2В2В1, А1А2В2В1,… АnА1В1Вn – боковые грани
Отрезки А1В1, А2В2…АnBn – боковые ребра призмы
Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников.

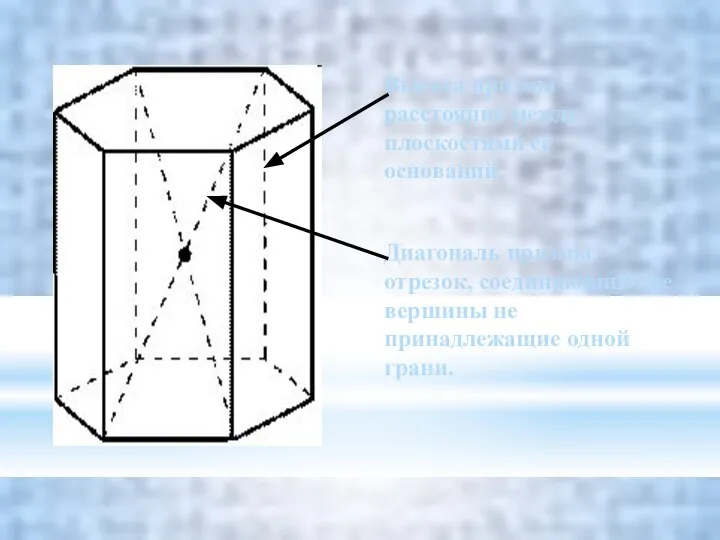
Высота призмы – расстояние между плоскостями её оснований.
Диагональ призмы – отрезок, соединяющий две вершины не принадлежащие одной грани.

Свойства призмы.
1. Основания призмы являются равными многоугольниками.
2. Боковые грани призмы являются параллелограммами.
3. Боковые ребра призмы равны.

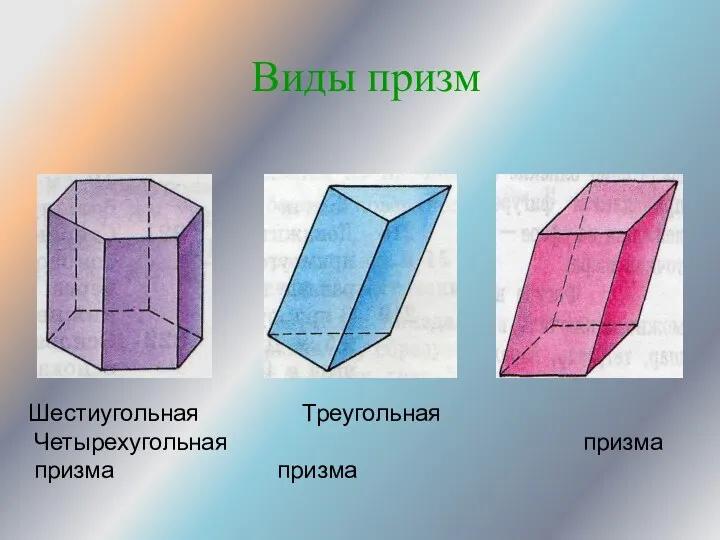
Виды призм
Шестиугольная Треугольная Четырехугольная призма призма призма

Наклонная и прямая призма
Если боковые ребра призмы перпендикулярны основаниям то призма называется прямой, в противном случае – наклонной.

Правильная призма
Призма называется правильной, если она прямая и ее основания - правильные многоугольники.

Боковой поверхностью призмы называется сумма площадей боковых граней.
Площадь боковой поверхности призмы

Площадь боковой поверхности прямой призмы
Теорема
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы, т.е на длину бокового ребра.
Sбок =Pоснования*h

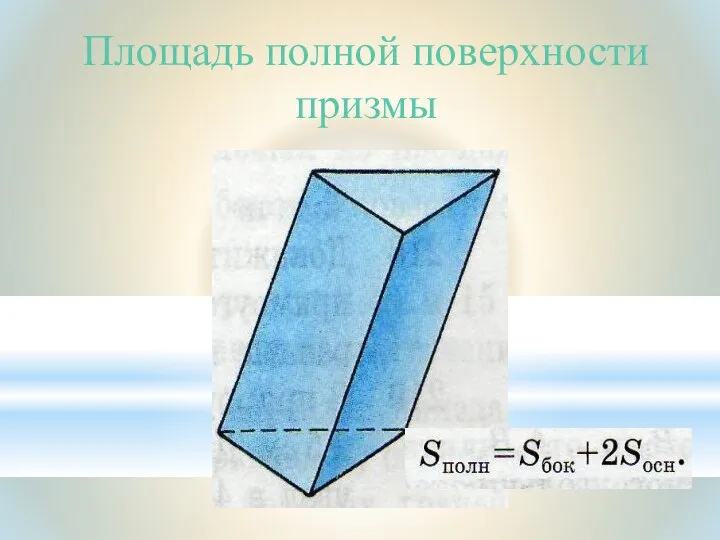
Площадь полной поверхности призмы

Объем призмы
вычисляется по формуле
где - площадь перпендикулярного сечения призмы,
или
где - площадь основания.