Применение производной к построению графиков функции

План исследования и построения
графика функции с помощью производной.
Найти область определения функции.
Найти производную функции.
Определить является ли функция чётной или является нечётной.
Найти точки экстремума .
Найти промежутки возрастания и убывания функции
Результаты исследования записать в виде таблицы. Найти несколько дополнительных точек графика функции. Построить график функции.

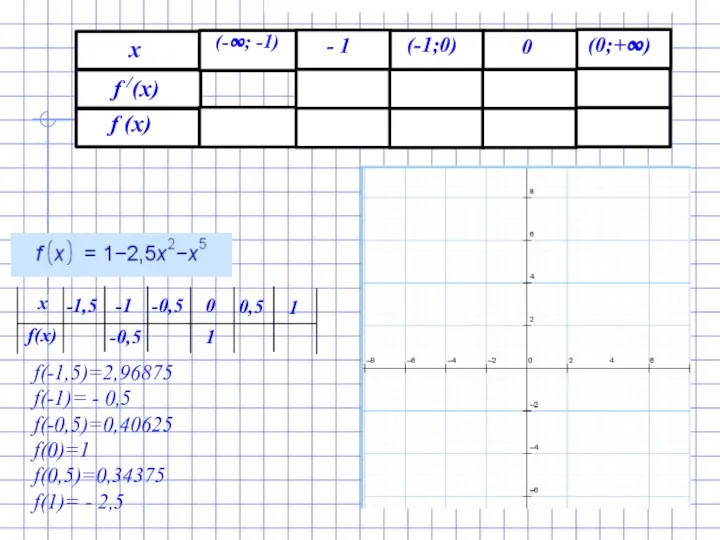
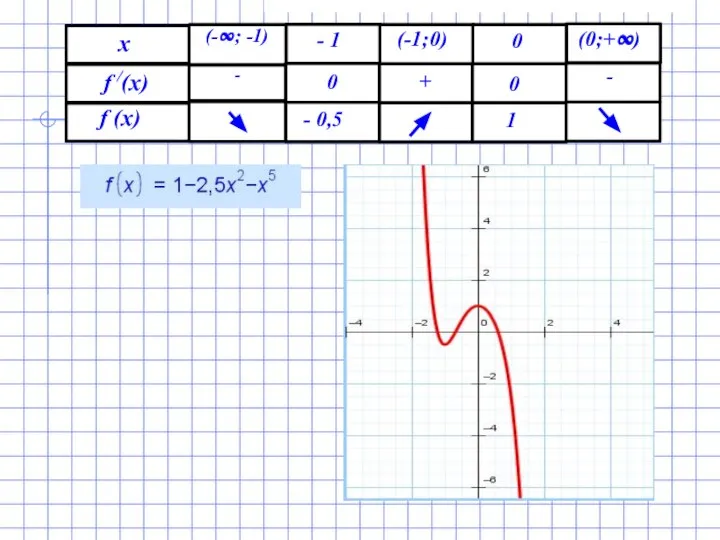
Исследование функции y=1-2,5x2-x5
и построения графика функции
у / = -5х-5х4
у / = -5х-5х4, у / = 0.
-5х-5х4=0
-5х(1+х3)=0
-5х=0 или (1+х3)=0
х=0:(-5) х3=0-1
х=0 х3=-1
х=∛-1
х= -1
х1=0 и х2= -1
стационарные точки.
у = 1-2,5х2-х5

1.(-∞; -1): f /(-2)= -5(-2) - 5(-2)4=10-80= -70, -70<0.
2.(-1;0): f /(-0,5)= -5(-0,5) - 5(-0,5)4=5/2-5/16=35/16, 35/16>0.
3.(0;+∞): f /(1)= -5(1) - 5(1)4= -5-5= -10, -10<0.
Функция возрастает на промежутке [-1;0].
Функция убывает на промежутке (-∞; -1], [0; +∞).
-
-
+

1.При переходе через стационарную точку -1 производная меняет знак с "-" на "+",
х2=-1 - точка минимума.
f(-1)=1-2,5(-1)2-(-1)5=1-2,5+1= -0,5.
2.При переходе через стационарную точку 0 производная меняет знак с "+" на "-",
х1=0 - точка максимума.
f(0)=1-2,5(0)2-(0)5=1-0-0=1.

f(-1,5)=2,96875
f(-1)= - 0,5
f(-0,5)=0,40625
f(0)=1
f(0,5)=0,34375
f(1)= - 2,5