Примеры комбинаторных задач

Такие задачи получили название комбинаторных задач, а раздел математики, в котором рассматриваются эти задачи, называют комбинаторикой.
В науке и на практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций.

Раздел математики,
в котором изучают
комбинаторные задачи,
называется
комбинаторикой

- раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов.
о

Термин «комбинаторика» был введён в математический обиход немецким философом, математиком Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».

Познакомимся с некоторыми
приемами решения комбинаторных задач
решение методом перебора;
решение с помощью дерева возможных вариантов;
решение с помощью комбинаторного правила умножения;
решение с помощью таблиц;
решение с помощью графов.

У Ирины 5 подруг: Вера, Зоя, Марина, Полина и Светлана. Она решила двух из них пригласить в кино. Укажите все возможные варианты выбора подруг. Сколько таких вариантов?
Замечание. При решении для краткости будем писать первые буквы имен.

Составим сначала все пары, в которые входит Вера.
ВЗ, ВМ, ВП, ВС
Выпишем теперь пары, в которые входит Зоя, но не входит Вера.
Далее составим пары, в которые входит Марина, но не входят Вера и Зоя.
Еще одна пара
ЗМ, ЗП, ЗС
МП, МС
ПС
Всего существует 4+3+2+1=10
Решение
Ответ:10 вариантов
Вера
Зоя
Марина
Полина
Света
Получим 4 пары.
Таких пар три.
Их две.
Далее составим пары, в которые входит Полина.

Рассмотрим еще одну задачу. На цветочной клумбе сидели шмель, жук, бабочка и муха. Два насекомых улетели. Какие пары насекомых могли улететь? Укажите все возможные варианты. Сколько таких вариантов?
Способ рассуждений, которым мы воспользовались при решении задачи, называют
перебором возможных вариантов.
ш
ж
б
м

Решение
Всего 3+2+1=6
Ответ:6 вариантов
ш
ш
ш
ж
ж
б
б
б
ж
м
м
м

Таким образом, из трёх данных цифр можно составить всего 9 различных двузначных чисел.
Ответ: 9 чисел.
Приемы решения комбинаторных задач
метод перебора
11;14;17; (начали с 1)
Решение: Для того, чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания:
Сколько двузначных чисел можно составить, используя цифры 1; 4; 7?
41;44;47; (начали с 4)
71;74;77; (начали с 7)

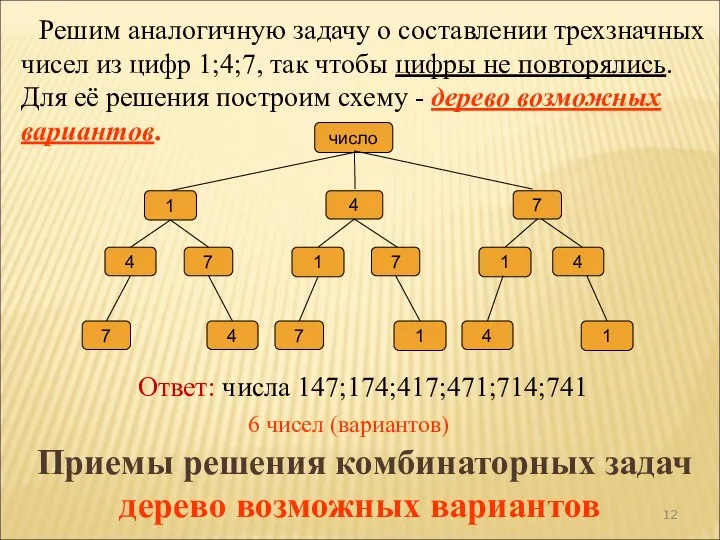
Приемы решения комбинаторных задач дерево возможных вариантов
Решим аналогичную задачу о составлении трехзначных чисел из цифр 1;4;7, так чтобы цифры не повторялись. Для её решения построим схему - дерево возможных вариантов.
число
1
4
7
4
4
7
7
1
1
7
7
1
1
4
4
Ответ: числа 147;174;417;471;714;741
6 чисел (вариантов)

Заметим, что ответ на вопрос, можно получить, не выписывая сами числа. Будем рассуждать так.
Первую цифру можно выбрать тремя способами. Так как после выбора первой цифры останутся две, то вторую цифру можно выбрать двумя способами. Остается приписать одну цифру. Следовательно, общее число искомых трехзначных чисел равно произведению

«Если объект А можно выбрать m способами, а другой объект В можно выбрать k способами, то объект «А и В» можно выбрать m ∙ k способами».
Мы нашли ответ на вопрос, используя так называемое комбинаторное правило умножения

У Куклы Светы 3 юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций одежды имеется у Светы?
Решение. 3·5 = 15
комбинаторное правило умножения

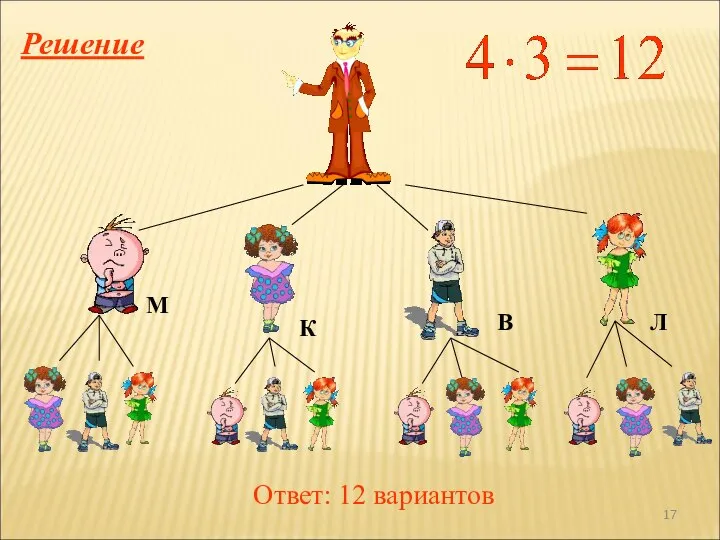
Решите задачу, используя
дерево возможных вариантов
В класс пришли четыре новых ученика Миша, Катя, Вася, Лиза. С помощью дерева возможных вариантов покажи, все возможные варианты расположения четырех учеников за одной партой. Сколько вариантов выбора будет?
Л
В
К
М

Ответ: 12 вариантов
Решение
М
В
К
Л

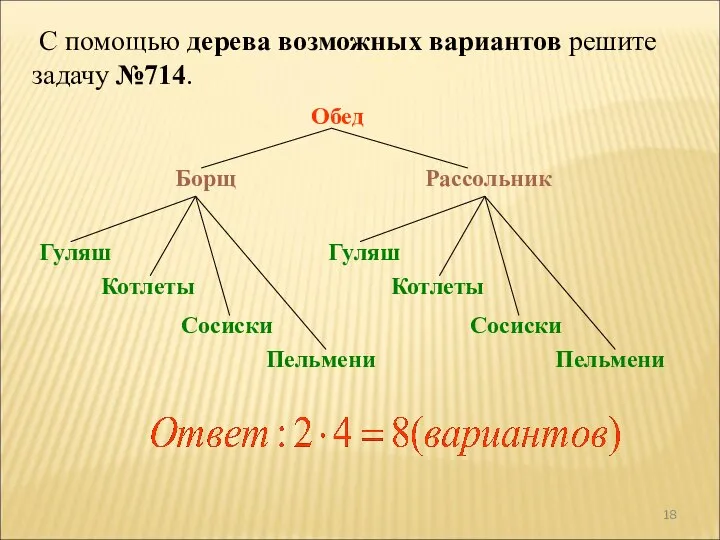
С помощью дерева возможных вариантов решите задачу №714.
Котлеты
Гуляш
Рассольник Борщ
Обед
Пельмени
Сосиски
Котлеты
Гуляш
Пельмени
Сосиски

У Миши 4 ручки разного цвета и 3 блокнота разного размера. Сколько различных наборов из ручки и блокнота сможет составить Миша? Реши задачу, составив таблицу.
Приемы решения комбинаторных задач
задачи, решаемые с помощью таблиц
м
с
б
с
з
ч
к

12 различных наборов
м
с
б
з
ч
к
с

Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9?
Приемы решения комбинаторных задач
задачи, решаемые с помощью таблиц
Ответ:15 чисел (5·3)
1
2
4
5
9
0
2
4
10
14
12
20
22
24
40
42
44
50
52
54
90
92
94

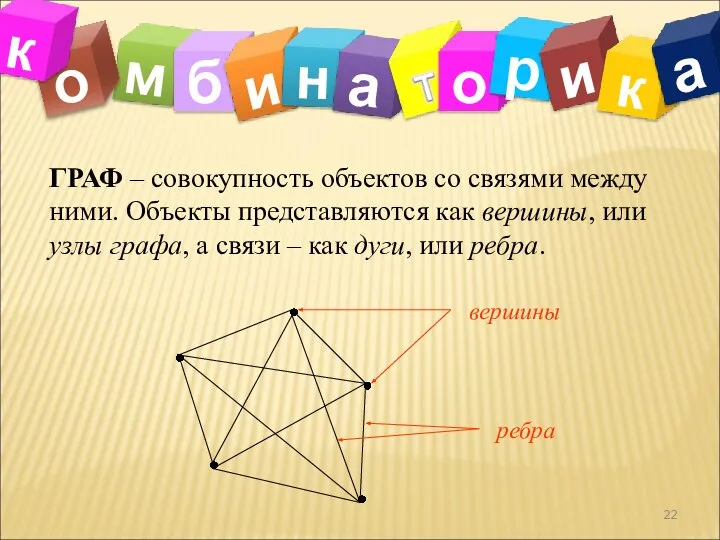
о
ГРАФ – совокупность объектов со связями между ними. Объекты представляются как вершины, или узлы графа, а связи – как дуги, или ребра.
вершины
ребра

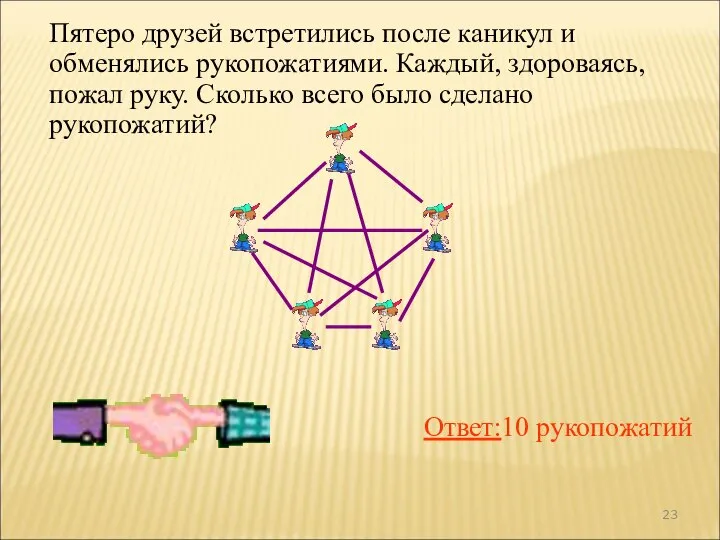
Пятеро друзей встретились после каникул и обменялись рукопожатиями. Каждый, здороваясь, пожал руку. Сколько всего было сделано рукопожатий?
Ответ:10 рукопожатий

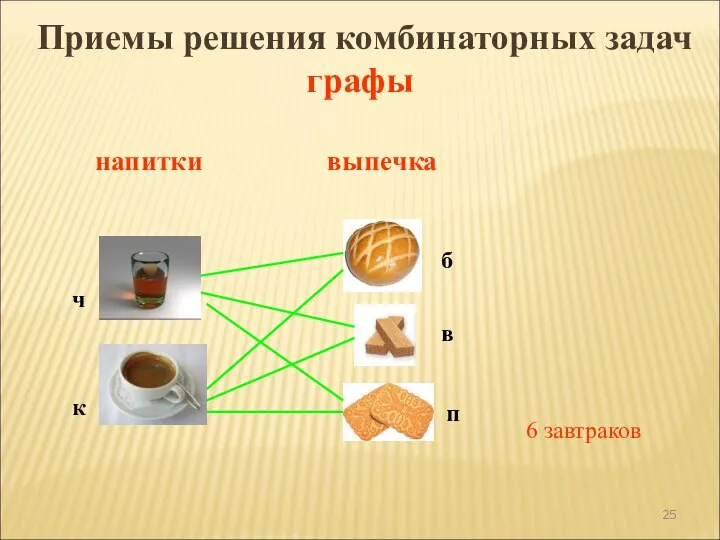
Сколько различных завтраков, состоящих из 1 напитка и 1 вида выпечки, можно составить из чая, кофе, булочки, печенья и вафель?
Решите задачу, используя граф
ч
к
б
п
в

6 завтраков
напитки
выпечка
ч
к
б
п
в
Приемы решения комбинаторных задач графы

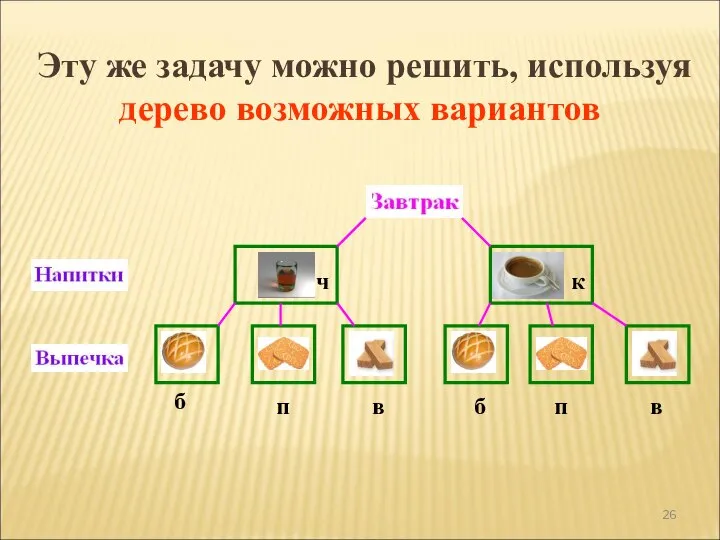
ч
к
б
б
п
п
в
в
Эту же задачу можно решить, используя дерево возможных вариантов

ч
ч
ч
ч
к
к
к
к
п
п
п
б
б
б
в
в
в
Решение задачи с помощью таблицы

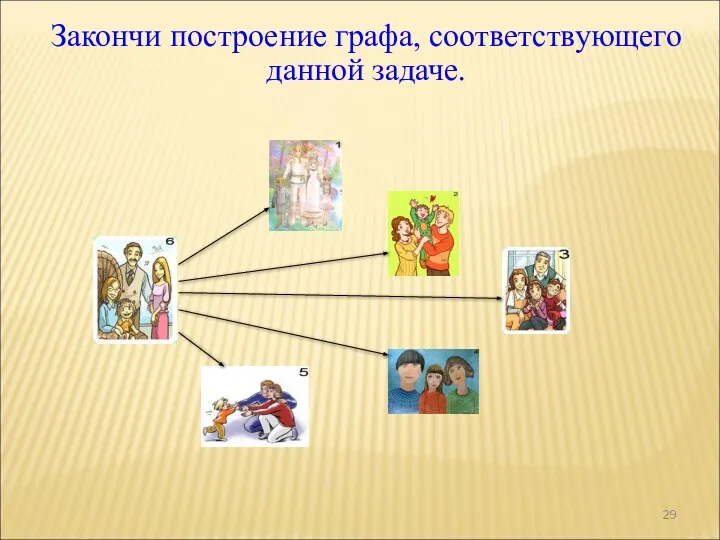
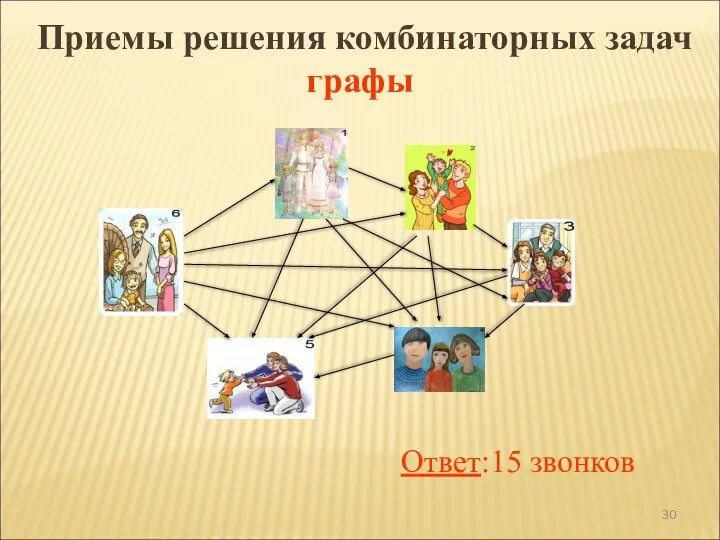
Шесть семей уехали отдыхать в разные города. Приехав к месту отдыха, они поговорили друг с другом по телефону. Сколько звонков было сделано?
Решите задачу, используя граф

Закончи построение графа, соответствующего данной задаче.

Приемы решения комбинаторных задач графы
Ответ:15 звонков

–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
Ответ:15 звонков
Приемы решения комбинаторных задач
задачи, решаемые с помощью таблиц

ДОМАШНЕЕ ЗАДАНИЕ:
§ 33, Примеры
№ 33.2, 33.5, 33.8, 33.10, 33.12.

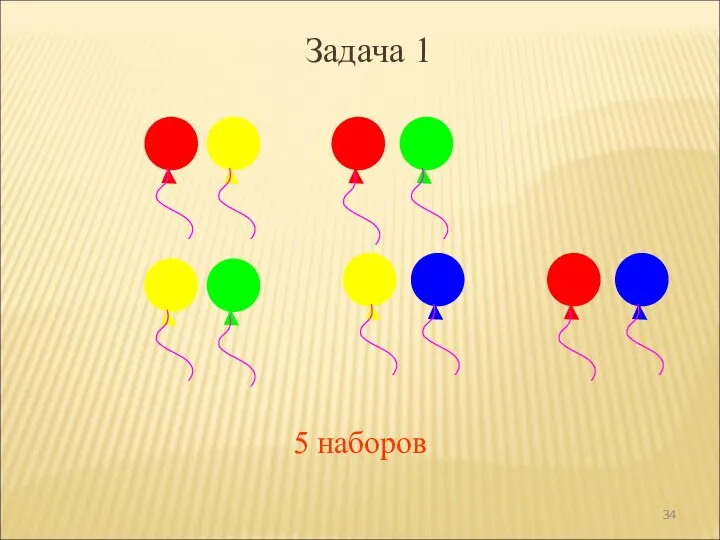
В магазине продают воздушные шары: красные, желтые, зеленые, синие. Какие наборы можно составить из двух разных шаров? Сколько наборов
у тебя получилось?
Задачи, решаемые
методом
организованного перебора
Приемы решения комбинаторных задач
дополнительные задачи
Задача 1

Задача 1
5 наборов

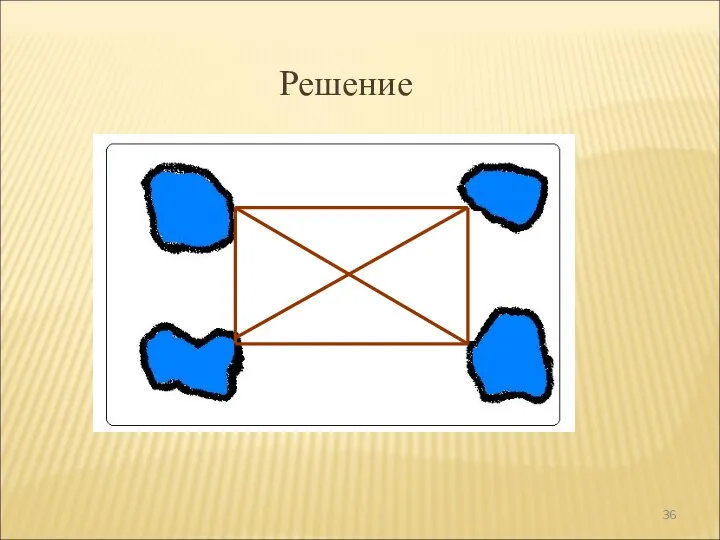
Приемы решения комбинаторных задач
Задача 2
В парке 4 пруда. Было решено засыпать песком дорожки между ними так, чтобы можно было пройти от одного пруда к другому кратчайшим путем, т.е. не нужно было идти в обход.
Задание: покажи, какие дорожки надо сделать.
Графы

Решение

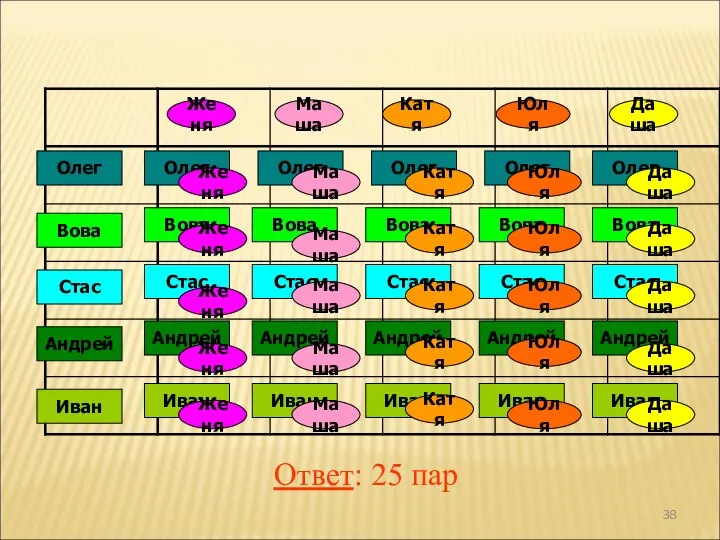
В танцевальном кружке занимаются пять девочек: Женя, Маша, Катя, Юля и Даша и
пять мальчиков: Олег, Вова, Стас, Андрей и Иван. Сколько различных танцевальных пар можно составить? Заполни таблицу.
Приемы решения комбинаторных задач
Задачи, решаемые
с помощью таблиц

Ответ: 25 пар
Женя
Маша
Катя
Юля
Даша
Олег
Вова
Стас
Андрей
Иван
Олег
Олег
Олег
Олег
Олег
Вова
Вова
Вова
Вова
Вова
Стас
Стас
Стас
Стас
Стас
Андрей
Андрей
Андрей
Андрей
Андрей
Иван
Иван
Иван
Иван
Иван
Женя
Женя
Женя
Женя
Женя
Маша
Маша
Маша
Маша
Маша
Катя
Катя
Катя
Катя
Катя
Юля
Юля
Юля
Юля
Юля
Даша
Даша
Даша
Даша
Даша

Задачи, решаемые с помощью таблиц
На завтрак Миша может выбрать: плюшку, бутерброд, пряник, или кекс, а запить он может: кофе, соком, кефиром. Сколько возможных вариантов завтрака?
Ответ:12 (4·3=12)