Содержание
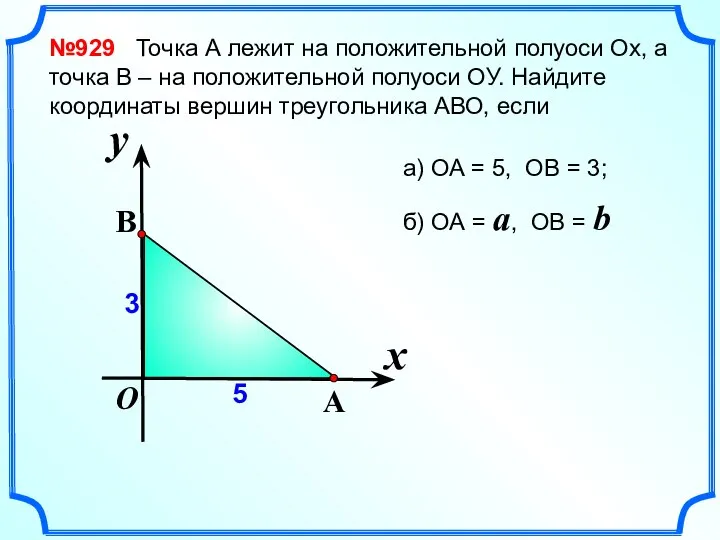
- 2. №929 Точка А лежит на положительной полуоси Ох, а точка В – на положительной полуоси ОУ.
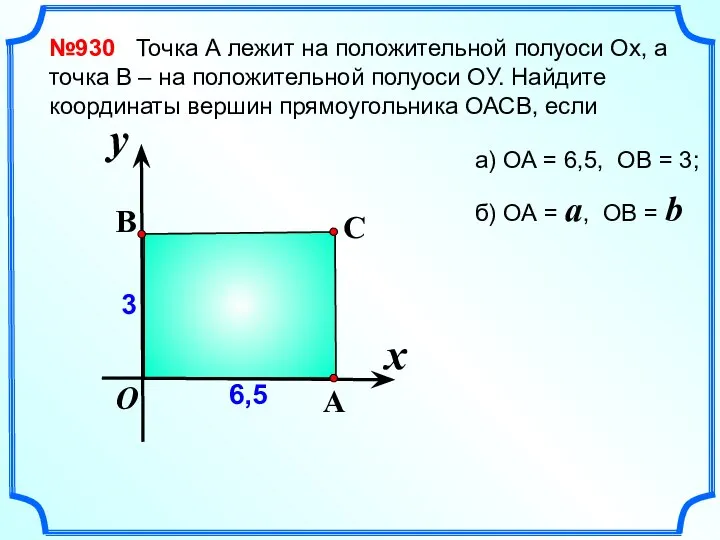
- 3. №930 Точка А лежит на положительной полуоси Ох, а точка В – на положительной полуоси ОУ.
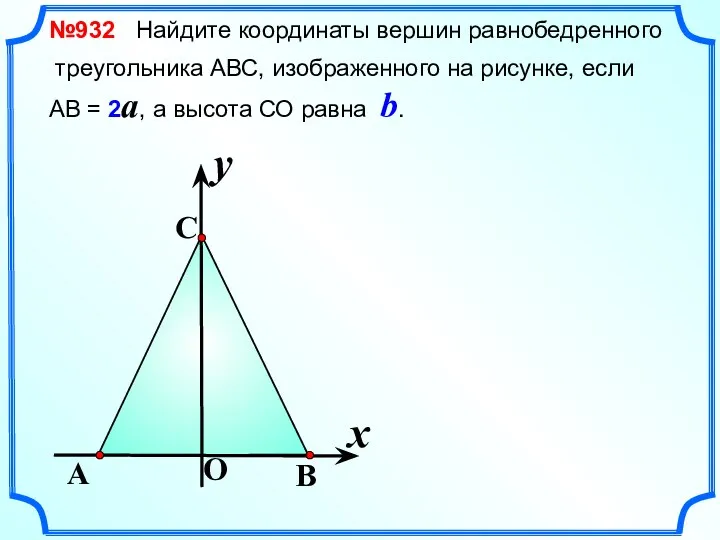
- 4. №932 Найдите координаты вершин равнобедренного треугольника АВС, изображенного на рисунке, если АВ = 2a, а высота
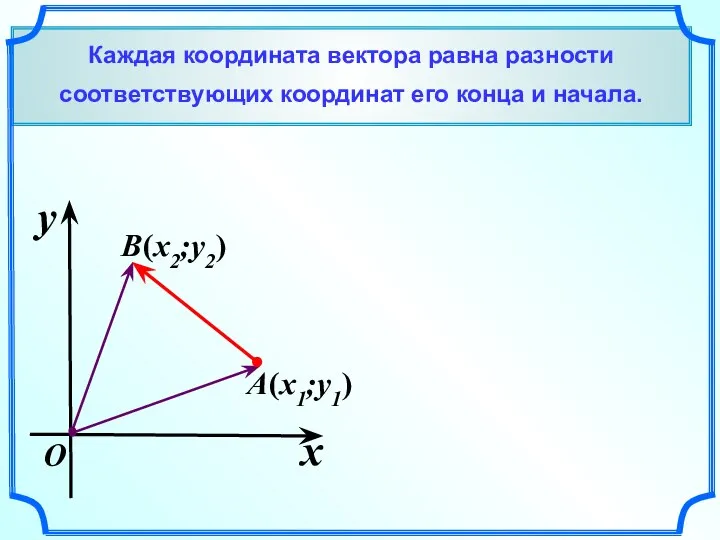
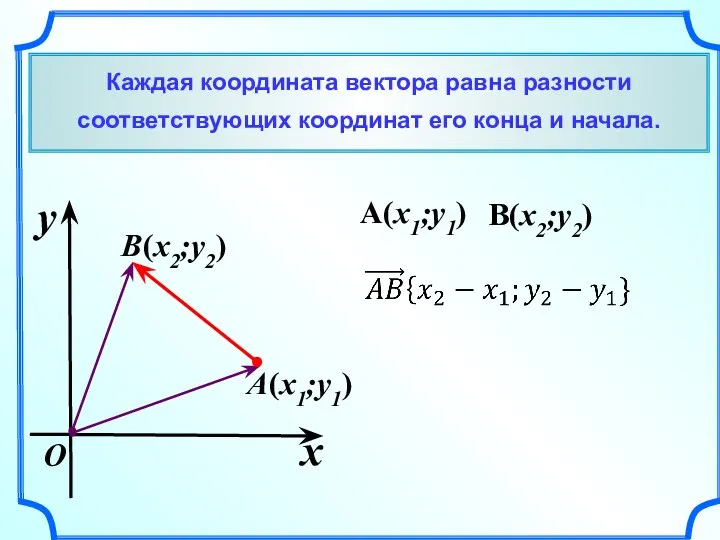
- 5. Каждая координата вектора равна разности соответствующих координат его конца и начала. x y O (x1;y1) (x2;y2)
- 6. Каждая координата вектора равна разности соответствующих координат его конца и начала. x y O (x1;y1) (x2;y2)
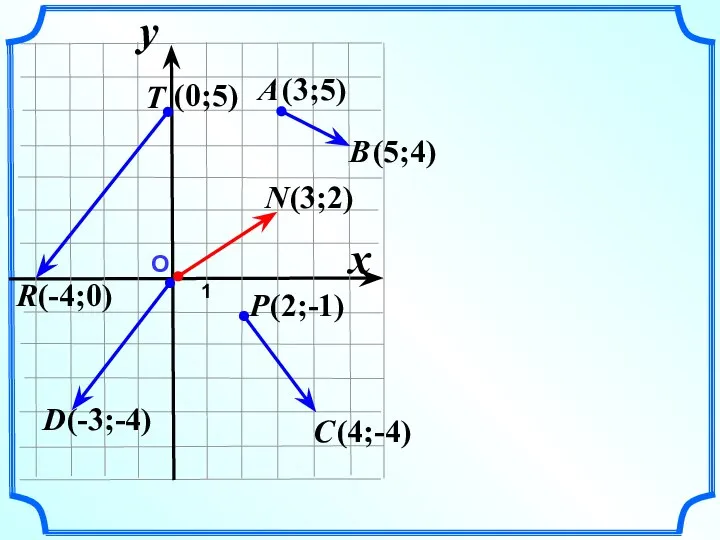
- 7. О 1 x y
- 8. Обратные задачи.
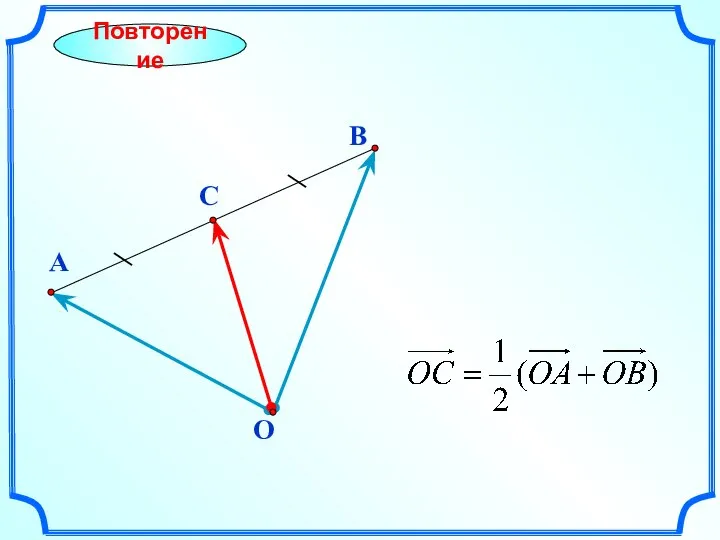
- 9. B Повторение A
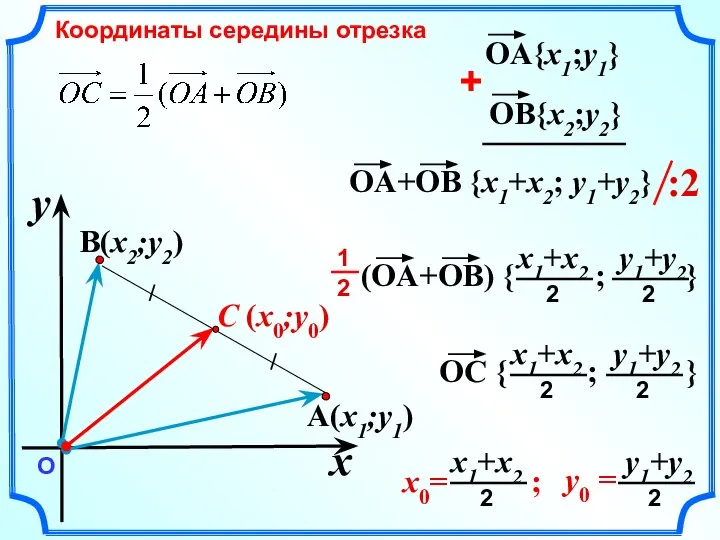
- 10. C (x0;y0) A(x1;y1) B(x2;y2) x y О Координаты середины отрезка
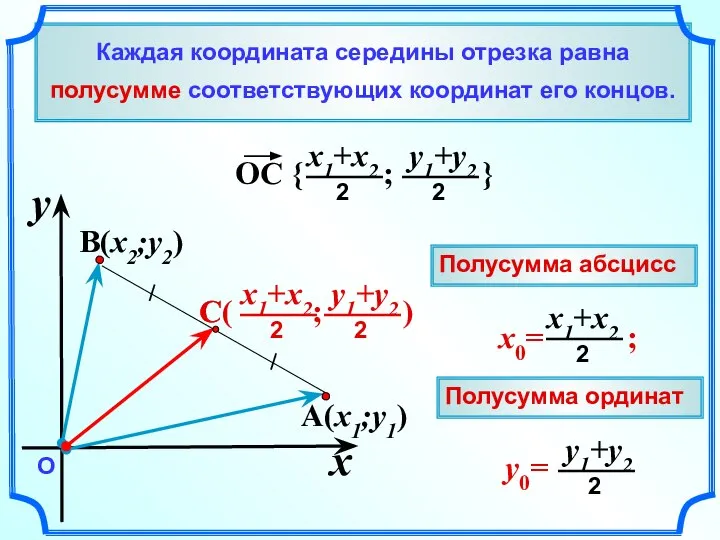
- 11. Каждая координата середины отрезка равна полусумме соответствующих координат его концов. A(x1;y1) B(x2;y2) x y О Полусумма
- 12. Каждая координата середины отрезка равна полусумме соответствующих координат его концов. A(x1;y1) B(x2;y2) C(x0;y0) C C –
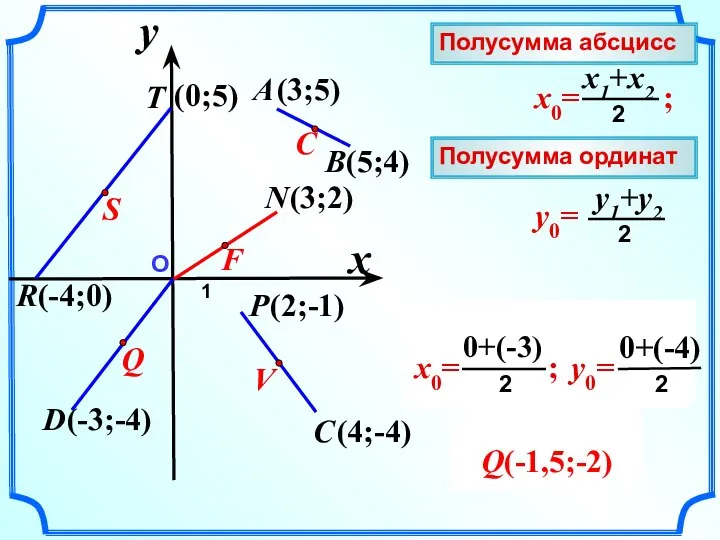
- 13. О 1 x y A (3;5) B(5;4) Полусумма абсцисс Полусумма ординат
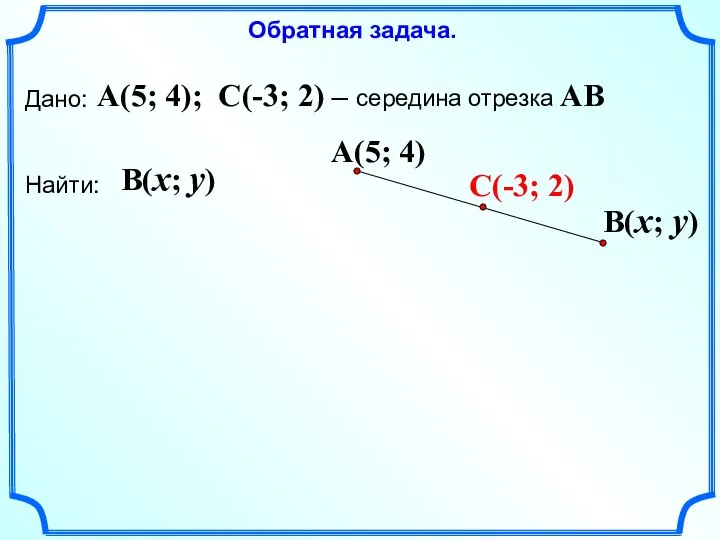
- 14. Дано: Найти: A(5; 4); C(-3; 2) – середина отрезка AB B(x; y) Обратная задача.
- 15. = = x y О Вычисление длины вектора по его координатам OA2=OA12 + AA12 OA2= x2
- 16. Вычисление длины вектора по его координатам вычисляется по формуле
- 17. Расстояние между двумя точками M2(x2;y2) M1(x1;y1) d
- 18. Расстояние между двумя точками и вычисляется по формуле
- 19. № 940 Найдите расстояние между точками A(2;7) и B(-2;7)
- 21. Скачать презентацию







 Решение задач всех типов на обыкновенные дроби
Решение задач всех типов на обыкновенные дроби Введение в математический анализ
Введение в математический анализ Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ  Восход и заход солнца с точки зрения графика тригонометрических функций
Восход и заход солнца с точки зрения графика тригонометрических функций Десятичные дроби. Уравнения
Десятичные дроби. Уравнения Таблица сложения
Таблица сложения Точечное оценивание параметров распределений случайных величин
Точечное оценивание параметров распределений случайных величин Преподаватель математики и информатики ГБОУ СПО РО «Константиновский педагогический колледж» Алексей Юлия Вадимовна
Преподаватель математики и информатики ГБОУ СПО РО «Константиновский педагогический колледж» Алексей Юлия Вадимовна Повторение вычисления двухзначных чисел столбиком с переходом через десяток
Повторение вычисления двухзначных чисел столбиком с переходом через десяток Теорема об интегрировании рядов Фурье
Теорема об интегрировании рядов Фурье Презентация. Ромб. Квадрат
Презентация. Ромб. Квадрат Презентация на тему Декартовы координаты (8 класс)
Презентация на тему Декартовы координаты (8 класс)  Построить линейный угол двугранного угла
Построить линейный угол двугранного угла Золотое сечение
Золотое сечение Генеалогическое древо семьи Бернулли
Генеалогическое древо семьи Бернулли Математикадан 5 класста үткәрелгән Тигезләмә темасын йомгаклау дәресе планы
Математикадан 5 класста үткәрелгән Тигезләмә темасын йомгаклау дәресе планы Сложение и вычитание чисел
Сложение и вычитание чисел Теоремы о пределах. Нахождение пределов
Теоремы о пределах. Нахождение пределов Метод интервалов. 8 класс
Метод интервалов. 8 класс Случайные величины
Случайные величины Среднее арифметическое. Задания
Среднее арифметическое. Задания Тела вращения. Открытый урок
Тела вращения. Открытый урок Диагонали треугольника равны
Диагонали треугольника равны Презентация на тему Правила вычисления производных
Презентация на тему Правила вычисления производных  Углы. Прямой и развернутый углы
Углы. Прямой и развернутый углы Распознавание и называние геометрических фигур
Распознавание и называние геометрических фигур Функция, ее график и свойства
Функция, ее график и свойства Линейная презентация
Линейная презентация