Корреляционный и спектральный анализ случайных процессов

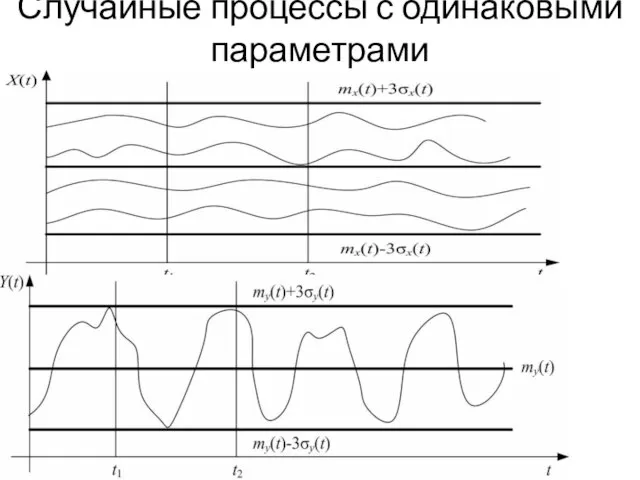
Случайные процессы с одинаковыми параметрами

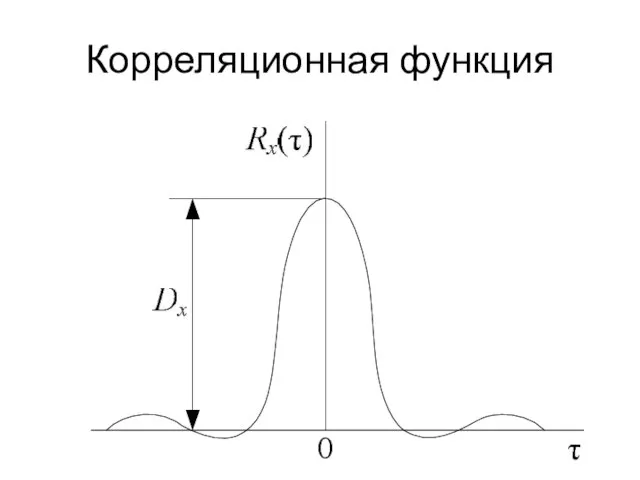
Корреляционная функция
Корреляционная функция – такая неслучайная функция Rx(t1, t2) двух аргументов, которая для любой пары фиксированных значений аргументов t1 и t2 равна корреляционному моменту, соответствующих этим сечениям случайных величин x(t1) и x(t2).

автокорреляционная функция
Корреляционная функция математически выражает корреляцию двух функций или корреляцию функции с самой собой (автокорреляционная функция).
где t1 и t2 – любые моменты времени

Корреляционные функции двух различных процессов
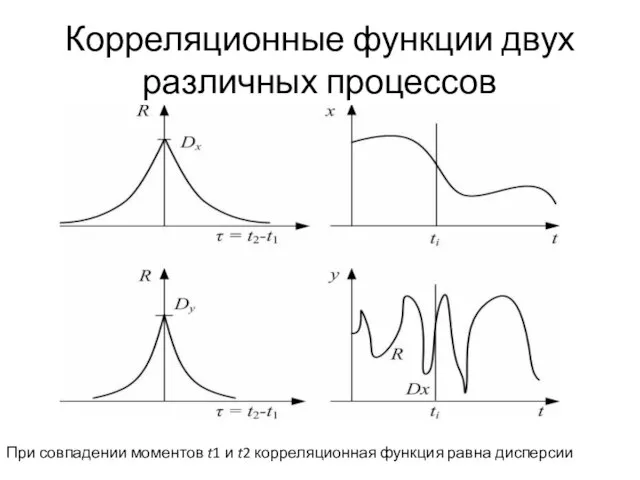
При совпадении моментов t1 и t2 корреляционная функция равна дисперсии

Нормированная корреляционная функция
Нормированная корреляционная функция вычисляется по формуле

Корреляционная функция
Знание о случайном процессе будет тем полнее, чем больше сечений будем рассматривать совместно и, следовательно, чем больше размерность плотности вероятности.
Следовательно рассматривая n сечений нужно знать n- мерную плотность.
Для полного описания случайного процесса необходимо знать бесконечномерную плотность вероятности. На практике обычно ограничиваются знанием первой и второй плотности вероятности.

Корреляционная функция
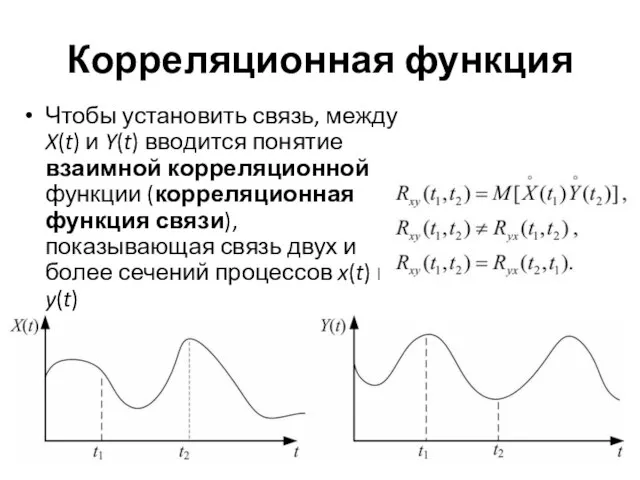
Чтобы установить связь, между X(t) и Y(t) вводится понятие взаимной корреляционной функции (корреляционная функция связи), показывающая связь двух и более сечений процессов x(t) и y(t)

корреляционная функция связи
нормированная корреляционная функция связи

Свойства корреляционных и взаимно корреляционных функций
Корреляционная функция Rx(t1, t2) симметрична относительно своих аргументов.
Корреляционная функция комплексной случайной функции при перестановке аргументов заменяется комплексной сопряжённой функцией.

Свойства корреляционных и взаимно корреляционных функций
При добавлении к случайной функции X(t) произвольного неслучайного слагаемого, корреляционная функция случайной величины не изменяется

Свойства корреляционных и взаимно корреляционных функций
При умножении случайной функции X(t) на произвольный неслучайный множитель ψ(t) корреляционная функция Rx(t1, t2) умножается на ψ(t1)ψ(t2).

Свойства корреляционных и взаимно корреляционных функций

Свойства корреляционных и взаимно корреляционных функций
Корреляционная функция является положительно определённой функцией
т.е. дисперсия случайной функции всегда неотрицательна.

Свойства корреляционных и взаимно корреляционных функций
Взаимная корреляционная функция двух случайных функций X(t) и Y(t) не изменяется при добавлении к этим случайным функциям произвольных неслучайных функций.

Свойства корреляционных и взаимно корреляционных функций

СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ СЛУЧАЙНЫХ ПРОЦЕССОВ
Спектр стационарного случайного процесса характеризует распределение дисперсий случайных амплитуд по частотам.
Спектральное разложение
является разложением случайной функции X(t) на конечном интервале наблюдения T

Коэффициенты разложения Zk, Uk, Ck определяются по формулам Эйлера- Фурье. Zk, Uk – некоррелированные центрированные случайные величины (амплитуды колебаний) с дисперсиями, одинаковыми для каждой пары случайных величин Zk и Uk с одним и тем же индексом k.
Координатными функциями разложения являются функции sin wkt и cos wkt при различных частотах wk.

Спектральное разложение
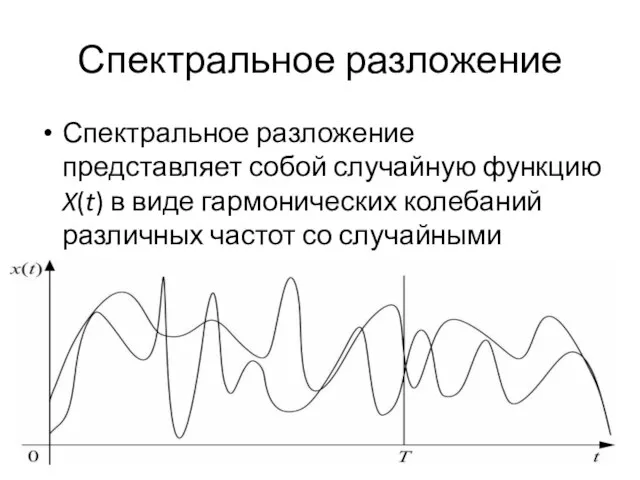
Спектральное разложение представляет собой случайную функцию X(t) в виде гармонических колебаний различных частот со случайными амплитудами

Для исследования спектрального разложения удобно представлять его в комплексной форме.

Корреляционный момент

корреляционная функция случайного процесса X (t)

корреляционная функция случайного процесса X (t)
Дисперсия случайной гармоники Xk(t) при представлении её в комплексной форме делится пополам между гармоникой положительной частоты wk и отрицательной частоты (–wk)

случайный процесс
представим случайный процесс X(t) в комплексной форме
Суммируем отдельно слагаемые, соответствующие положительным и отрицательным частотам.
Заметим, что сумму отрицательных слагаемых можно выразить таким же образом, как и сумму положительных слагаемых

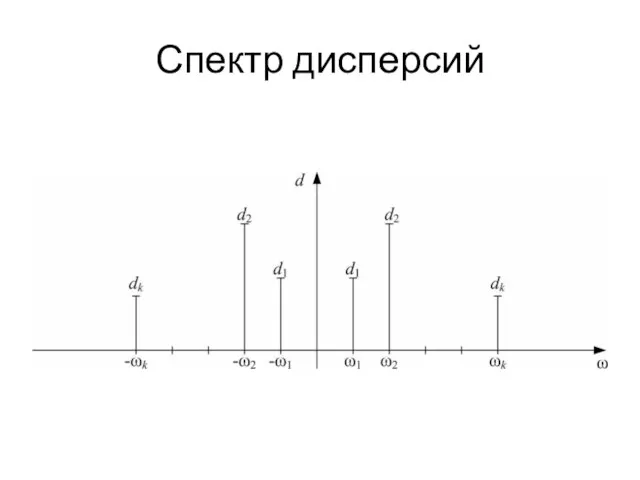
Спектр дисперсий
Распределение дисперсии по частотам определяет так называемый спектр дисперсий стационарной случайной функции.
Спектр дисперсий можно изобразить на графике в виде линейчатого спектра

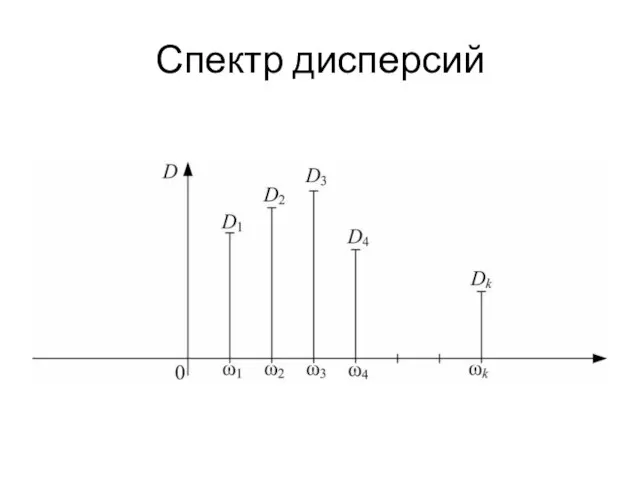
Спектр дисперсий

Спектр дисперсий
Так как отрицательные частоты физически не существуют.
можно переписать только для положительных частот
w1, w2, … wk. При этом дисперсии, соответствующие этим частотам, необходимо удвоить.

Спектр дисперсий

показывает, что дисперсия стационарного процесса X(t) равна дисперсий всех гармоник его спектрального разложения.
даёт разложение корреляционной функции Rx(τ) случайного процесса X(tв ряд Фурье, коэффициентами которого являются дисперсии dk. А dk вычисляются как коэффициенты ряда Фурье

Спектральное разложение стационарных случайных функций (процессов) в непрерывный спектр дисперсии
Для этого будем рассматривать X(t) при T стремящемуся к бесконечности. Тогда расстояния между опорными частотами будут неограниченно уменьшаться.
При этом дискретный спектр дисперсии будет неограниченно приближаться к непрерывному, в котором бесконечно малому интервалу частот Δωk = ωk – ωk–1 будет соответствовать элементарная дисперсия dk(ωk).

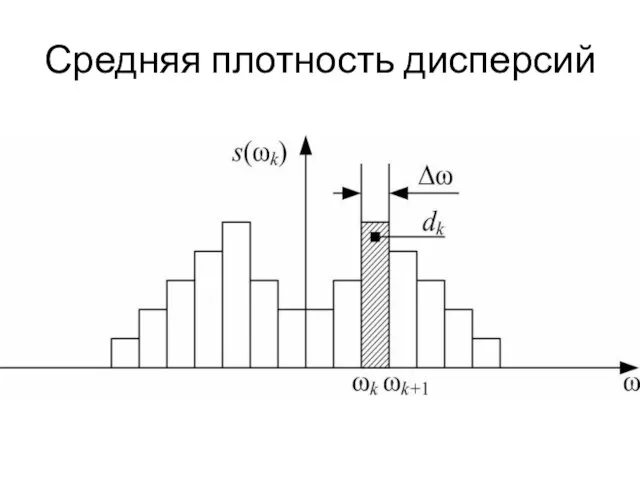
Средняя плотность дисперсий

спектральная плотность
dk/Δω имеет физический смысл средней плотности дисперсии и называется спектральной плотностью

Переход от дискретного спектра к непрерывному

Переход от дискретного спектра к непрерывному

Переход от дискретного спектра к непрерывному

Формула, выражающая корреляционную функцию стационарного случайного процесса через её спектральную плотность, была впервые получена в начале 30-х годов для ограниченного класса случайных процессов американским математиком, «отцом» кибернетики Норбертом Винером (1894- 1964).
Несколько позже эту формулу для любых стационарных случайных процессов вывел советский математик Александр Яковлевич Хинчин (1894- 1959).
Поэтому формулы, связывающие Rx(τ), Sx(w) называют формулами Винера-Хинчина.

плотность распределения дисперсии
Графический смысл предельного перехода от конечного интервала [0, T] к бесконечному при T → ∞, Δω → 0 выражается в том, что ступенчатая функция sx(wk) будет неограниченно приближаться к непрерывной функции sx(w), которая будет изображать плотность распределения дисперсии случайных амплитуд по частотам непрерывного спектра.

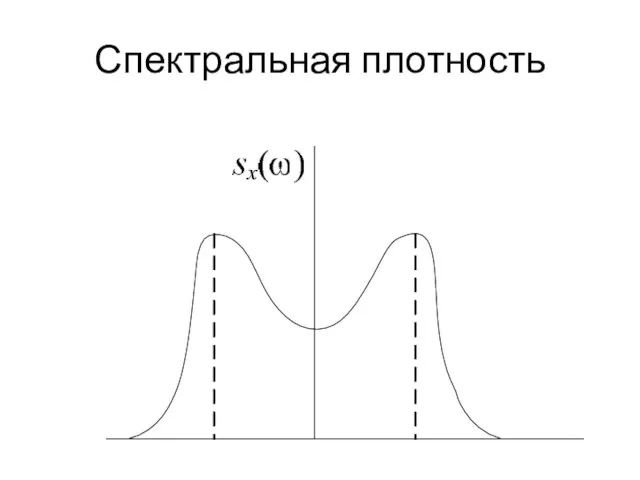
спектральной плотностью стационарного случайного процесса
Непрерывная функция sx(ω) называется спектральной плотностью стационарного случайного процесса. sx(ω) характеризует частотный состав стационарного случайного процесса X(t) и полностью определяется его корреляционной функцией Rx(τ)

Разложение дисперсии
представляет собой разложение дисперсии Dx на сумму элементарных слагаемых sx(ω)dω, каждая из которых представляет собой дисперсию, приходящуюся на элементарный бесконечно малый интервал частот dω, прилежащей к точке ω при (– ∞ < ω < ∞).

Спектральная плотность стационарного случайного процесса

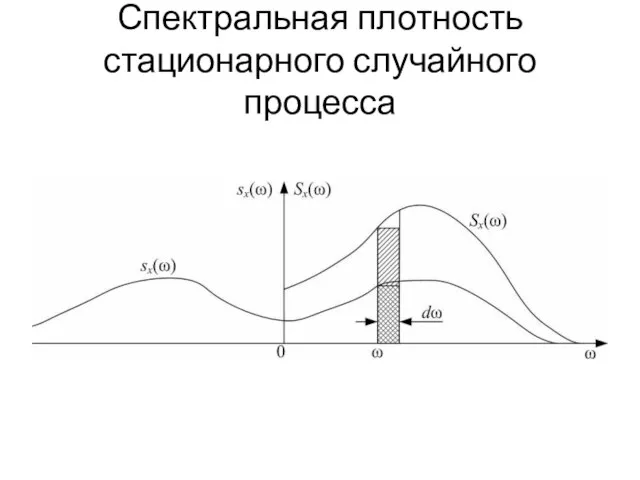
нормированная спектральная плотность

Свойства спектральной плотности
Спектральная плотность действительного стационарного случайного процесса является чётной действительной функцией аргумента ω
Дисперсия действительного стационарного случайного процесса равна интегралу от спектральной плотности этого процесса в бесконечных пределах

Спектральная плотность стационарного случайного процесса – функция неотрицательная.

Корреляционные функции и спектральные плотности типовых стационарных процессов
Белый шум
Формирующий фильтр
Нерегулярная качка

Белый шум
Белый шум – это центрированный случайный процесс X(t) с некоррелированными сечениями.
корреляционная функция белого шума

Белый шум
Множитель G(t) = G(t1) = G(t2) называется интенсивностью белого шума.
Если G(t) = G – белый шум стационарный.
Белый шум – идеализированная случайная функция, реализовать которую на практике невозможно.

спектральная плотность

Формирующий фильтр
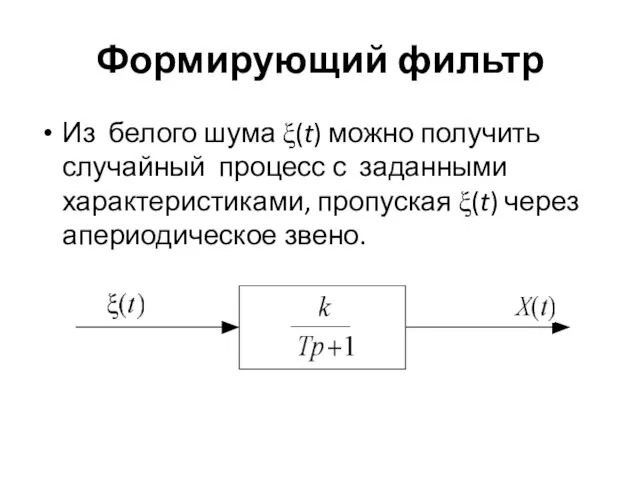
Из белого шума ξ(t) можно получить случайный процесс с заданными характеристиками, пропуская ξ(t) через апериодическое звено.

Корреляционная функция формирующего фильтра

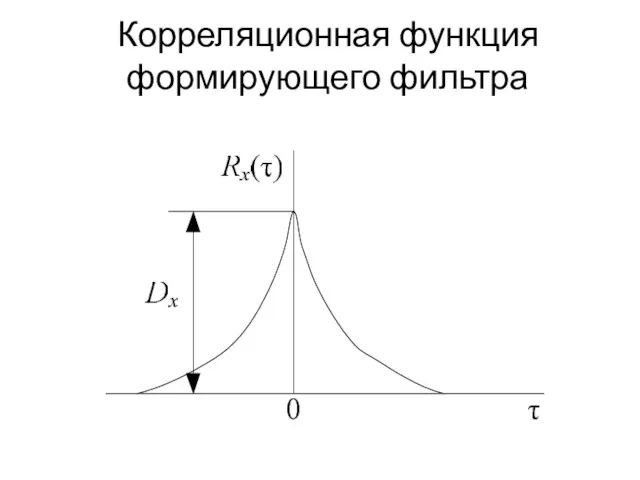
спектральная плотность формирующего фильтра

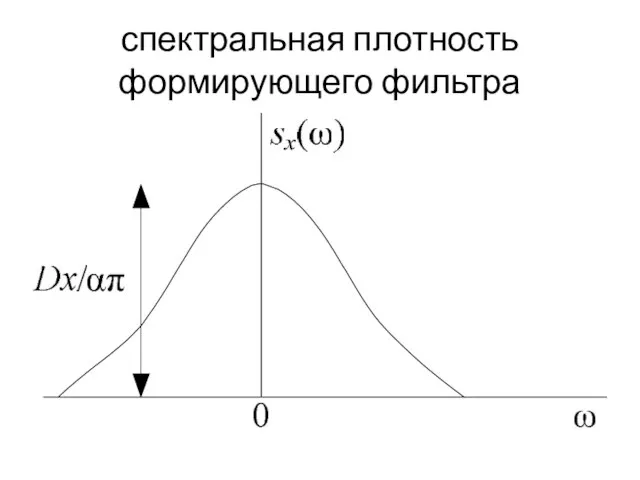
Экспоненциальная корреляционная функция

Спектральная плотность

Формирующий фильтр
При уменьшении параметра α (при возрастании постоянной времени Т) корреляционная функция будет убывать медленнее, что соответствует более плавным реализациям случайного процесса X(t).
Кривая sx(w) при этом вытягивается вверх, сжимаясь с боков, т.е. повышается удельный вес низких частот.
При α → ∞ (T → 0) X(t) вырождается в белый шум.

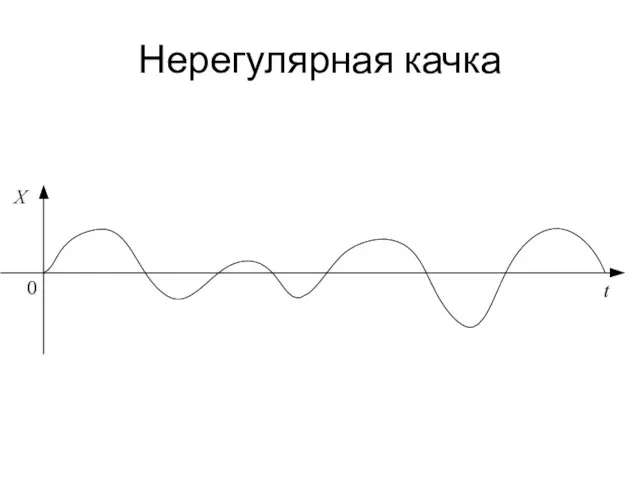
Нерегулярная качка
Некоторые объекты, например корабли, самолёты, находясь под действием нерегулярных возмущений (волнение моря, турбулентность атмосферы), движутся по случайному закону.
Получающееся при этом случайное движение объекта называют нерегулярной качкой, в отличие от регулярной качки, представляющей собой периодическое движение.

Нерегулярная качка

Корреляционная функция
Выражение является экспоненциально-косинусной корреляционной функцией, где ω0 – резонансная частота, α – параметр затухания, Dx – дисперсия.

Спектральная плотность

Корреляционная функция

Спектральная плотность