Содержание
- 2. ОПРЕДЛЕНИЕ. Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых
- 3. Высотой призмы называется расстояние между её основаниями. ВЫСОТА ПРИЗМЫ
- 4. Поверхность призмы Боковой поверхностью призмы (точнее боковой поверхности) называется сумма площадей боковых граней. Полная поверхность призмы
- 5. Свойства призмы Основания призмы равны. Основания призмы лежат в параллельных плоскостях. Боковые ребра призмы параллельны и
- 6. Виды призм Призма называется прямой, если её боковые рёбра перпендикулярны основаниям. В противном случае призма называется
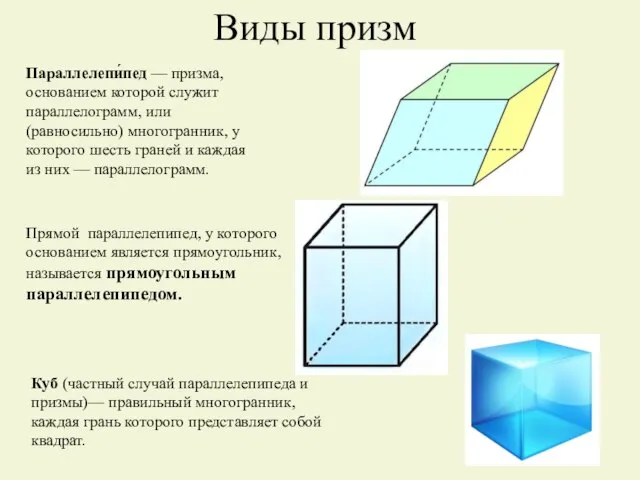
- 7. Виды призм Параллелепи́пед — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней
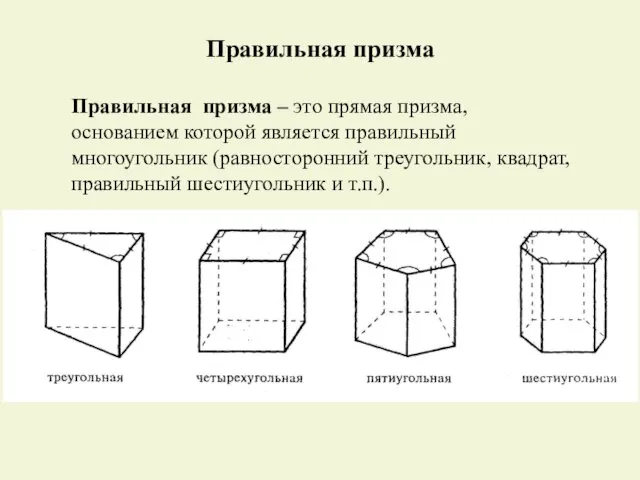
- 8. Правильная призма – это прямая призма, основанием которой является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник
- 10. Скачать презентацию





 Презентация на тему Степени
Презентация на тему Степени  Какие величины можно вычислить по следующим формулам
Какие величины можно вычислить по следующим формулам Выражение в инфиксной форме. Выражение в постфиксной форме
Выражение в инфиксной форме. Выражение в постфиксной форме Решение задач. 3 класс
Решение задач. 3 класс Практическая работа. Вычислить значения функции в критических точках и на концах отрезка
Практическая работа. Вычислить значения функции в критических точках и на концах отрезка Презентация на тему Площадь
Презентация на тему Площадь  Третий признак равенства треугольников
Третий признак равенства треугольников Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними
Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними Сколько останется? Посчитай и назови ответ
Сколько останется? Посчитай и назови ответ Арифметический квадратный корень. Классная работа
Арифметический квадратный корень. Классная работа Формула суммы n первых членов геометрической прогрессии
Формула суммы n первых членов геометрической прогрессии Возмущения линейных систем и проматрицы
Возмущения линейных систем и проматрицы Его величество п
Его величество п Векторное произведение векторов
Векторное произведение векторов Осевая и центральная симметрия
Осевая и центральная симметрия Структура арифметической задачи
Структура арифметической задачи Дискретная математика с элементами математической логики. Основы теории множеств
Дискретная математика с элементами математической логики. Основы теории множеств Графический способ решения линейных уравнений с модулями
Графический способ решения линейных уравнений с модулями Окружность
Окружность Десятичные дроби
Десятичные дроби Площадь параллелограмма
Площадь параллелограмма Задача предельного типа. Мир арифметики
Задача предельного типа. Мир арифметики Комплексные числа. Основные понятия
Комплексные числа. Основные понятия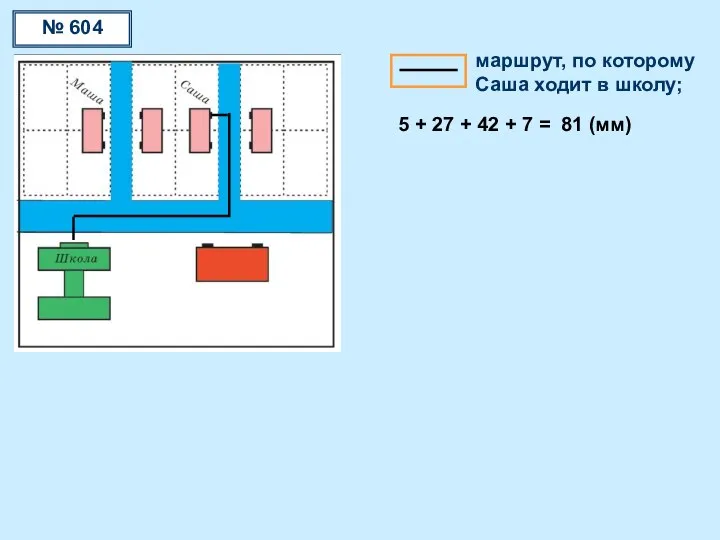 Длина маршрута (задача)
Длина маршрута (задача) Эконометрика. Временные ряды
Эконометрика. Временные ряды Свойства квадратного корня
Свойства квадратного корня Арифметический квадратный корень. Самостоятельная работа
Арифметический квадратный корень. Самостоятельная работа Делители и кратные
Делители и кратные