элементы теории множеств

Ключевые слова
множество
подмножество
объединение множеств
пересечение множеств
дополнение

Понятие множества
Множество — совокупность объектов произвольной природы, которая рассматривается как единое целое.
!

Способы задания множества
Попробуйте описать эти множества словесно, указав характеристическое свойство их элементов.
?

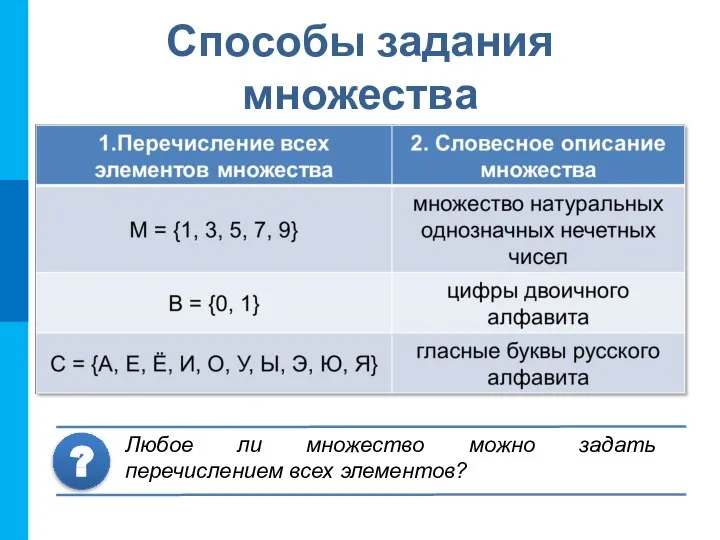
Способы задания множества
Любое ли множество можно задать перечислением всех элементов?
?

Способы задания множества
1 способ – для задания конечных множеств
2 способ – для задания любых множеств
!

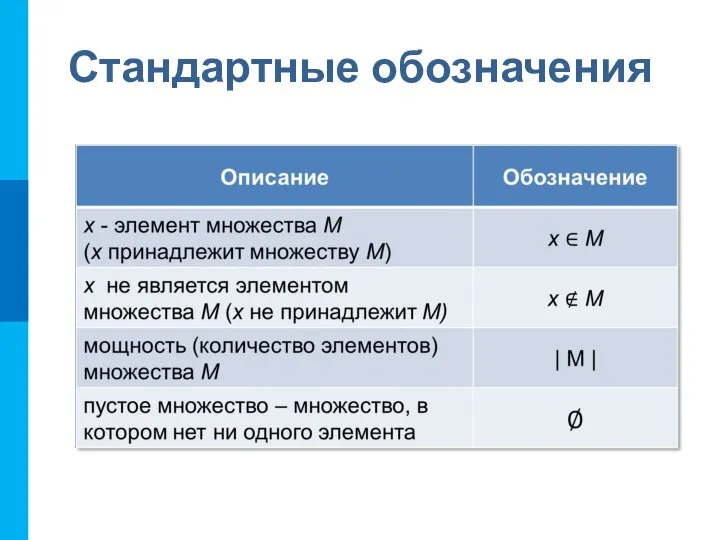
Стандартные обозначения
Множества принято обозначать прописными буквами латинского алфавита (A, B, C, …).
Объекты, входящие в состав множества, называются его элементами и обозначаются строчными латинскими буквами.

Стандартные обозначения

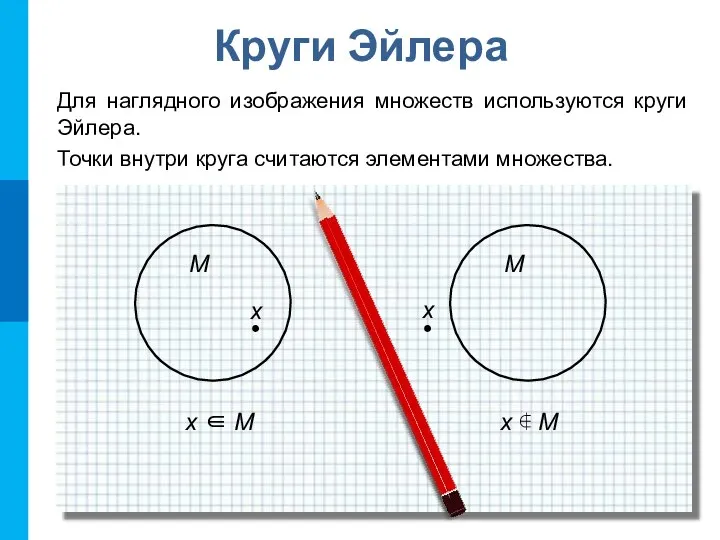
Круги Эйлера
Для наглядного изображения множеств используются круги Эйлера.
Точки внутри круга считаются элементами множества.
x ∈ M
x ∉ M

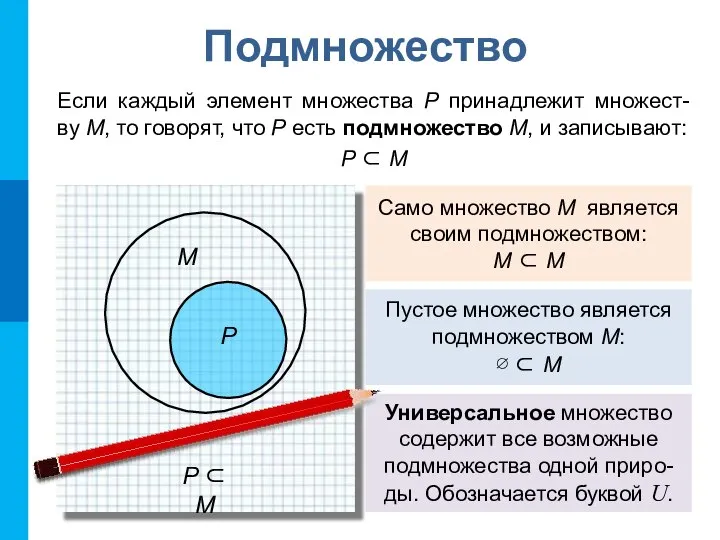
Подмножество
Если каждый элемент множества P принадлежит множест-
ву М, то говорят, что P есть подмножество М, и записывают:
P ⊂ М
Само множество М является своим подмножеством:
М ⊂ М
Пустое множество является подмножеством М:
∅ ⊂ М
Универсальное множество содержит все возможные подмножества одной приро-ды. Обозначается буквой U.
P ⊂ М

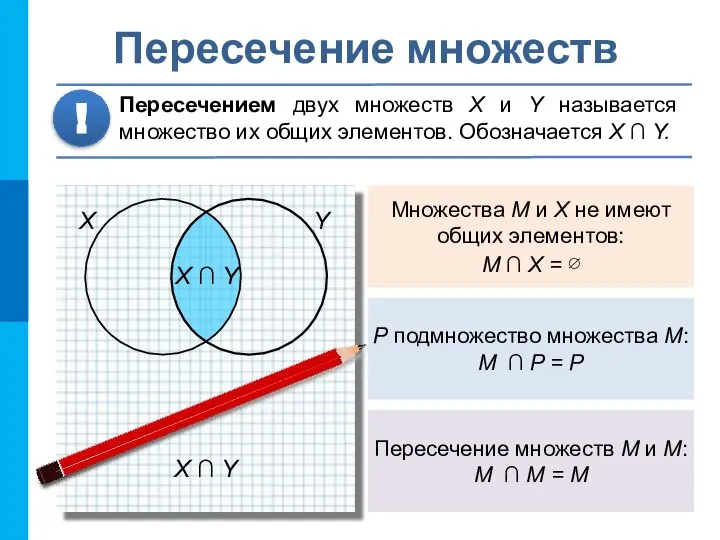
Множества M и X не имеют общих элементов:
M ∩ X = ∅
P подмножество множества М:
М ∩ P = P
Пересечение множеств М и М:
М ∩ М = М
X ∩ Y
Пересечение множеств
Пересечением двух множеств X и Y называется множество их общих элементов. Обозначается X ∩ Y.
!
X
Y
X ∩ Y

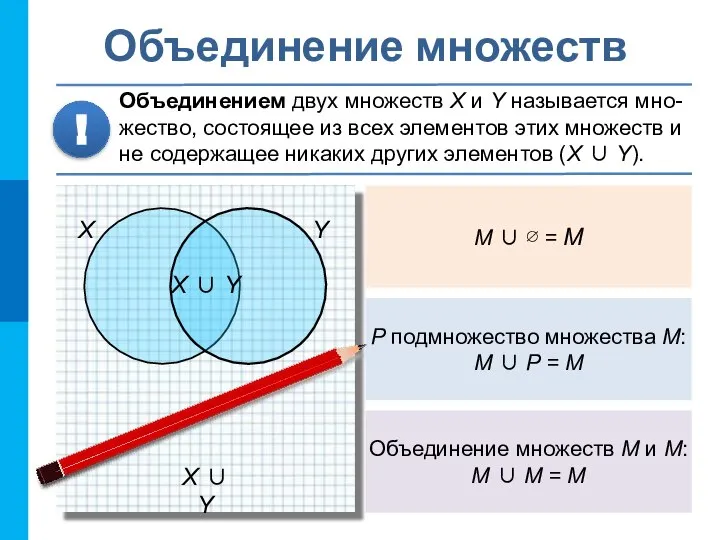
X ∪ Y
Объединение множеств
Объединением двух множеств X и Y называется мно-жество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов (X ∪ Y).
!
M ∪ ∅ = М
P подмножество множества М:
М ∪ P = М
Объединение множеств М и М:
М ∪ М = М

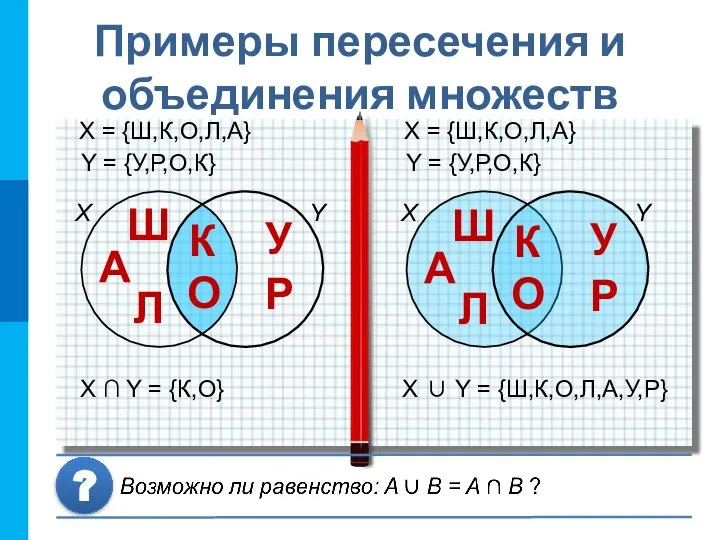
Примеры пересечения и объединения множеств
X
Y
X ∪ Y = {Ш,К,О,Л,А,У,Р}
X = {Ш,К,О,Л,А}
Y = {У,Р,О,К}
X ∩ Y = {К,О}
X
Y
Ш
Л
А
К
О
У
Р
Ш
Л
А
К
О
У
Р
?
X = {Ш,К,О,Л,А}
Y = {У,Р,О,К}

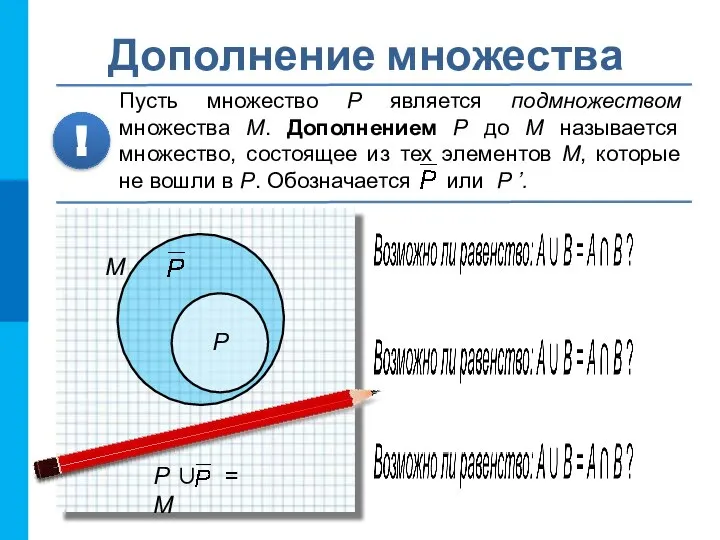
Дополнение множества
Пусть множество P является подмножеством множества М. Дополнением P до М называется множество, состоящее из тех элементов М, которые не вошли в P. Обозначается или P ’.
!
P ∪ = M

Мощность множества
Мощностью конечного множества называется число его элементов.
Мощность множества X обозначается |X|.
!
Мощность любого конечного множества равно количеству элементов данного множества.

Вопросы и задания
Задайте путем перечисления всех элементов множество O всех цифр, используемых для записи чисел в восьмеричной системе счисления.
Задайте путем перечисления всех элементов множество К всех цепочек из 0 и 1, состоящих ровно из трёх символов.
Проверка
Проверка

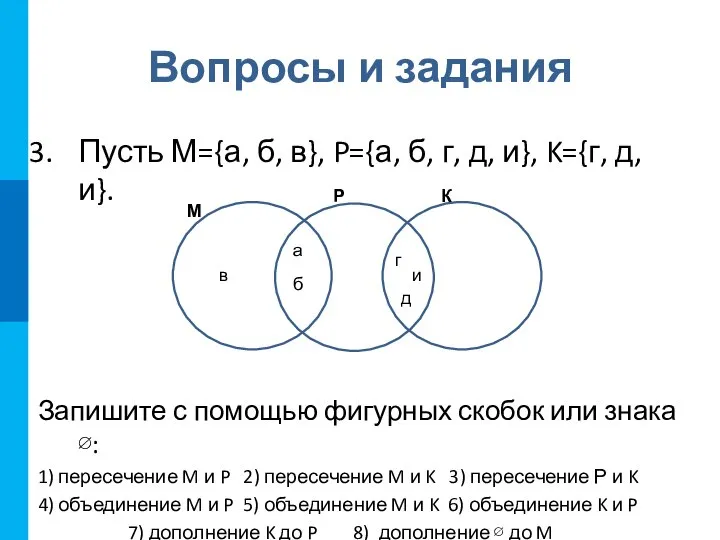
Вопросы и задания
Пусть М={а, б, в}, P={а, б, г, д, и}, K={г, д, и}.
Запишите с помощью фигурных скобок или знака ∅:
1) пересечение M и P 2) пересечение M и K 3) пересечение Р и K
4) объединение M и P 5) объединение M и K 6) объединение K и P
7) дополнение K до P 8) дополнение ∅ до M
а
б
в
д
г
и
М
Р
К

Вопросы и задания

Самое главное
Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое.
Пересечением двух множеств X и Y называется множество их общих элементов.
Объединением двух множеств X и Y называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов.
Пусть множество P является подмножеством множест-
ва М. Дополнением P до М называется множество, состоящее из тех элементов М, которые не вошли в P.
Мощностью конечного множества называется число его элементов.

Информационные источники
http://www.unikru.ru/userfiles/zoo-animal-friends-angela-waye.jpg
http://download.4-designer.com/files/20140221/Childlike-cartoon-alphabet-vector-material-62504.jpg
http://s4.pic4you.ru/y2014/07-04/12216/4477117.png
http://azbukadekor.ru/upload/iblock/475/475cddb0ce49566682e02adfdffd946e.jpg
http://st.gdefon.com/wallpapers_original/s/580857_babochki_raznotsvetnyie_radujnyie_5500x3765.jpg
https://pixabay.com/static/uploads/photo/2013/07/12/13/16/pencil-146715__180.png

Множество О всех цифр, используемых для записи чисел в восьмеричной системе счисления:
О = {0, 1, 2, 3, 4, 5, 6, 7}
К задачам