Содержание
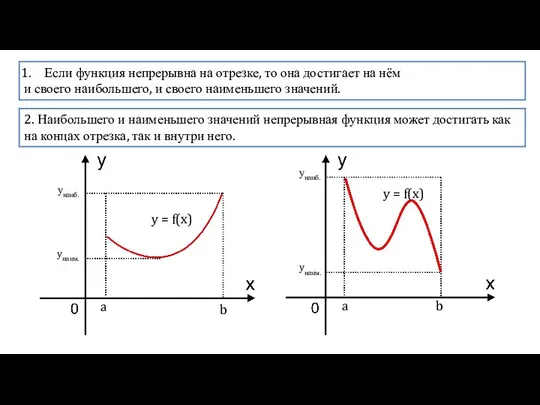
- 2. Если функция непрерывна на отрезке, то она достигает на нём и своего наибольшего, и своего наименьшего
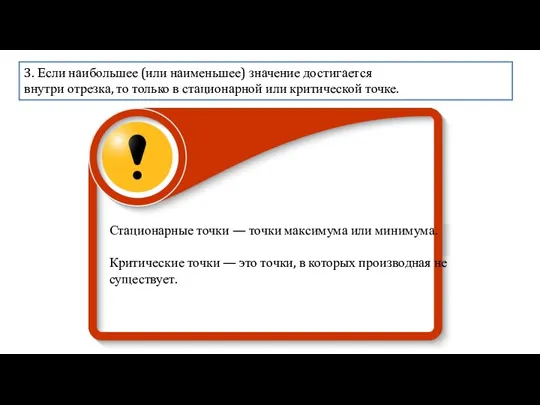
- 3. 3. Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
- 4. Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у = f(x) на отрезке [a, b]: 1)
- 5. Решение. 1) 2) у'= 0; х1 = 1, х2 = –1.
- 6. 3) yнаим. = 4, х = 1;
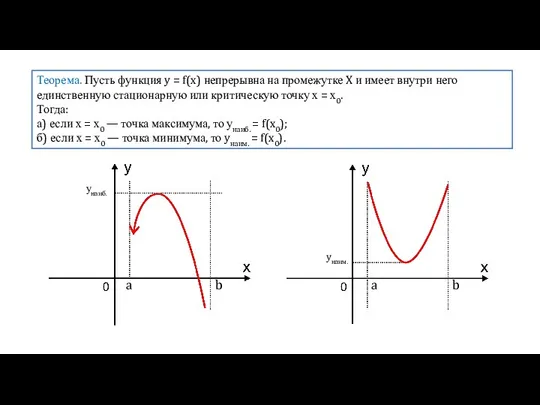
- 7. Теорема. Пусть функция y = f(x) непрерывна на промежутке X и имеет внутри него единственную стационарную
- 8. Решение. 1) у‘ = 0; х = –3, х = 2;
- 10. Скачать презентацию




 Периметр квадрата
Периметр квадрата Тригонометрия. Восхождение на пик
Тригонометрия. Восхождение на пик Ответы к тестам для подготовки к ЕГЭ по математике
Ответы к тестам для подготовки к ЕГЭ по математике Сложение двух векторов
Сложение двух векторов Основные понятия комбинаторики. Факториал. Вычисление факториала
Основные понятия комбинаторики. Факториал. Вычисление факториала Признаки равенства треугольников
Признаки равенства треугольников Урок математики в 3 классе
Урок математики в 3 классе Производная. Правила нахождения производных. Производная степенной функции с действительным показателем
Производная. Правила нахождения производных. Производная степенной функции с действительным показателем Теорема Пифагора. Чертеж к доказательству Пифагора
Теорема Пифагора. Чертеж к доказательству Пифагора Сложение и вычитание многочленов
Сложение и вычитание многочленов Применение производной к построению графиков функций
Применение производной к построению графиков функций Деревья
Деревья Думаємо колективно, працюємо оперативно, сперечаємось доказово – це для всіх обов'язково
Думаємо колективно, працюємо оперативно, сперечаємось доказово – це для всіх обов'язково Интегрирование неотрицательніх измериміх функций
Интегрирование неотрицательніх измериміх функций ТРАПЕЦІЯ
ТРАПЕЦІЯ Решение задач на работу
Решение задач на работу Решение простейших логарифмических неравенств
Решение простейших логарифмических неравенств Алгоритм решения линейных уравнений
Алгоритм решения линейных уравнений Угол. Прямой и развернутый угол. Чертежный треугольник
Угол. Прямой и развернутый угол. Чертежный треугольник Площадь треугольника
Площадь треугольника Функции многих переменных. Лекция 16
Функции многих переменных. Лекция 16 Цилиндр. Круговой цилиндр
Цилиндр. Круговой цилиндр Метод геометрических рядов и точные решения дифференциально-разностных уравнений
Метод геометрических рядов и точные решения дифференциально-разностных уравнений Использование свойств действий при вычислениях. Наглядный материал к уроку
Использование свойств действий при вычислениях. Наглядный материал к уроку Презентация по математике "Дроби в Древнем Риме" -
Презентация по математике "Дроби в Древнем Риме" - 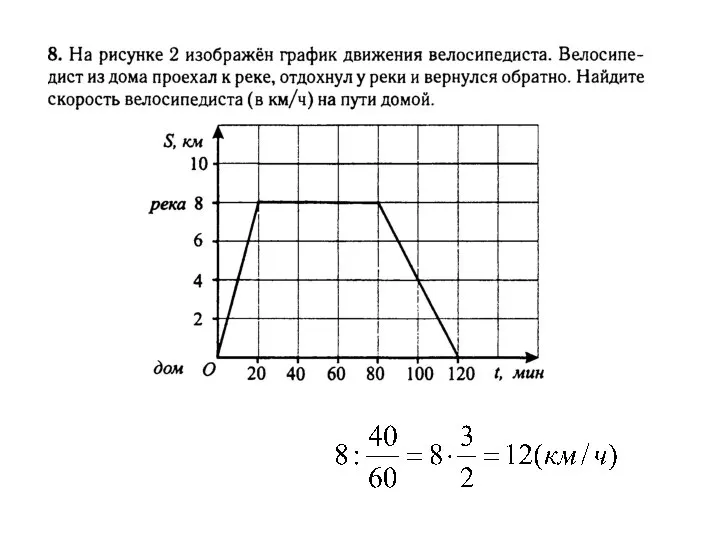 Линейная функция. Задания
Линейная функция. Задания Навыки решения составных задач
Навыки решения составных задач Решение треугольников
Решение треугольников