Содержание
- 2. Прямоугольный параллелепипед
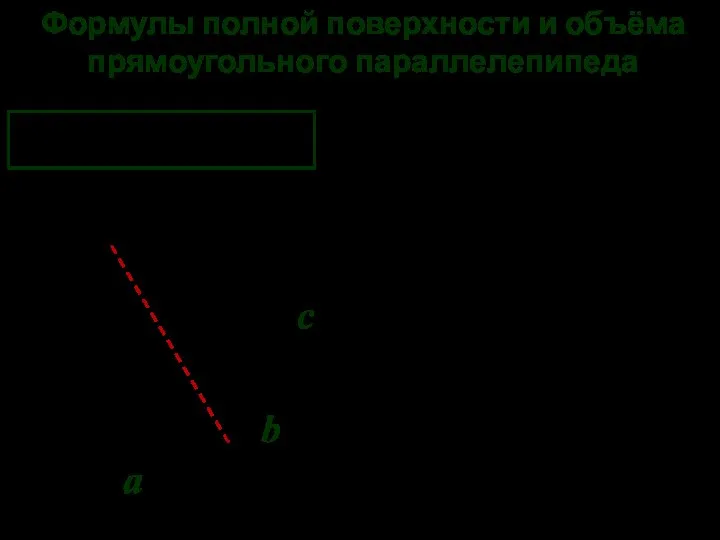
- 3. b Формулы полной поверхности и объёма прямоугольного параллелепипеда a c d
- 4. №1. 16+25+9 = 50.
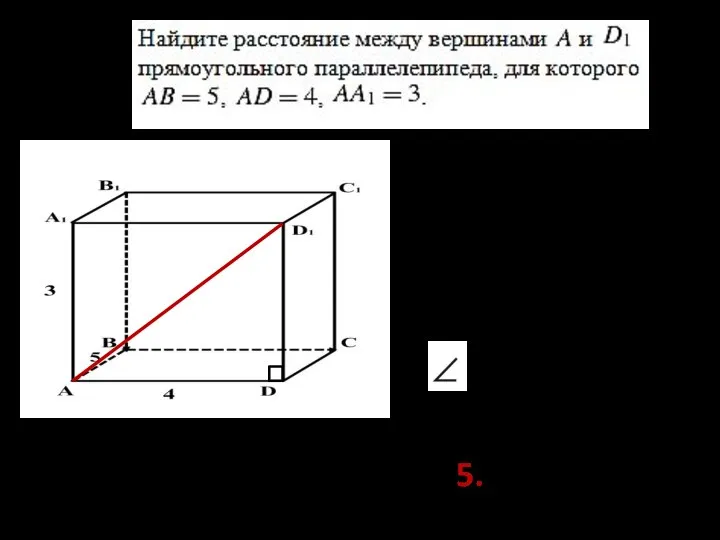
- 5. №2. D = 90°
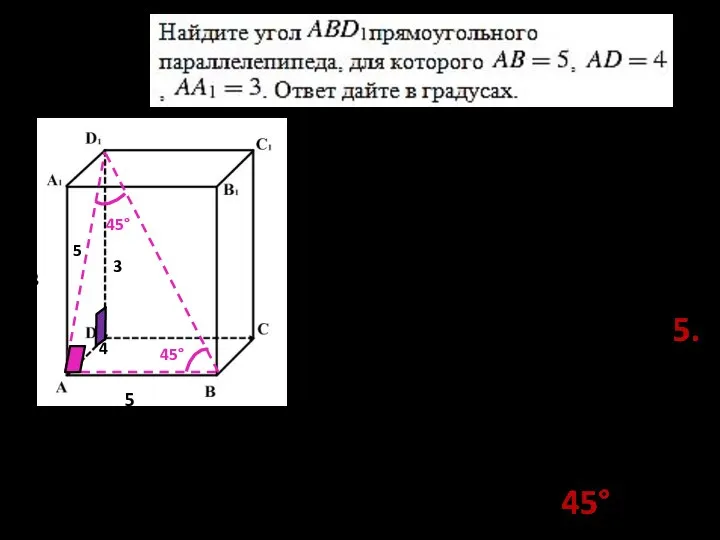
- 6. №3. 3 4 5 D= 90° ; 3 5 B = 45°; 45° 45° A =
- 7. №4. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого
- 8. 5. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна
- 9. 6. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности Т.к сфера единичная, то R=1.
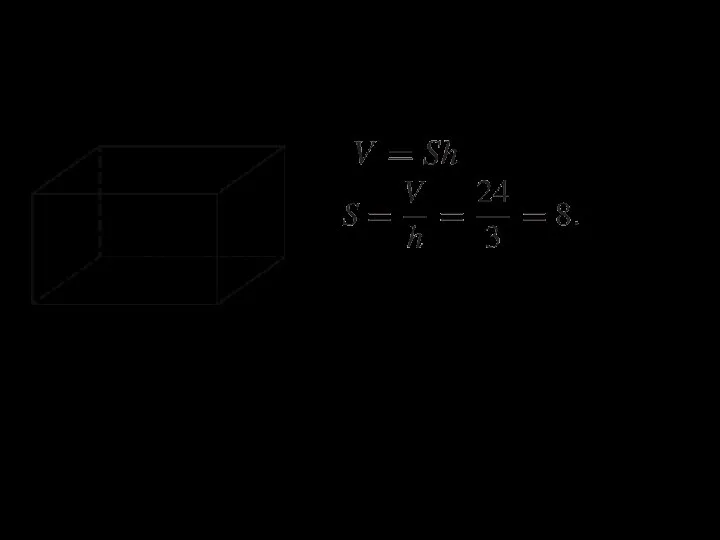
- 10. 7. Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
- 11. 8. Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда,
- 12. 9. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен
- 13. 10.Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему
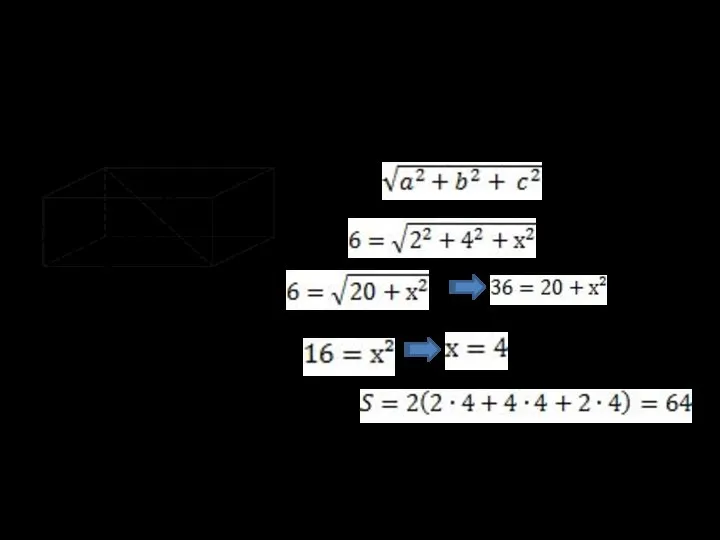
- 14. 11. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6.
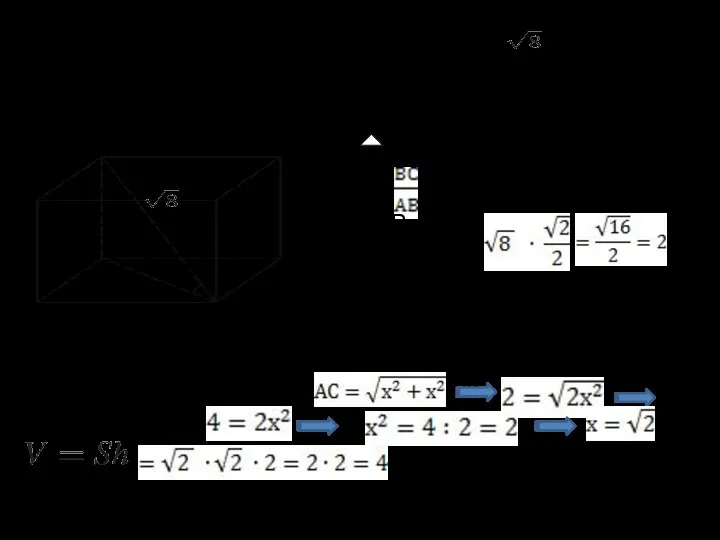
- 15. 12. Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна и образует с плоскостью этой
- 16. 13. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6.
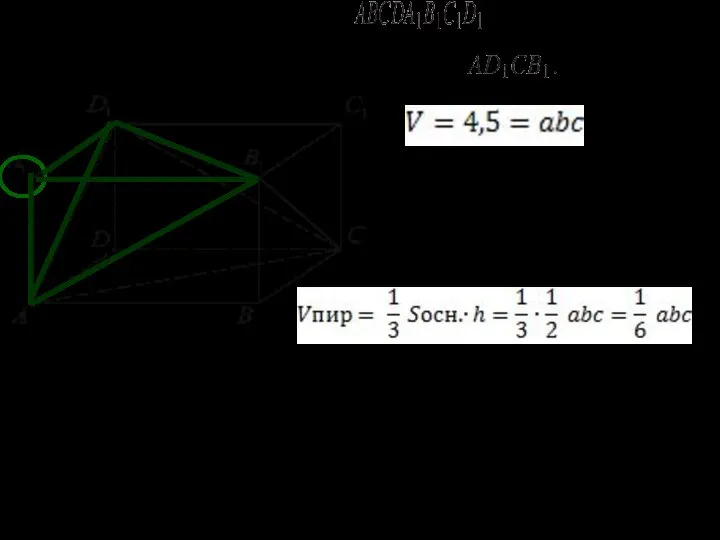
- 17. 14. Объем параллелепипеда равен 4,5. Найдите объем треугольной пирамиды
- 18. 14. Объем параллелепипеда равен 4,5. Найдите объем треугольной пирамиды
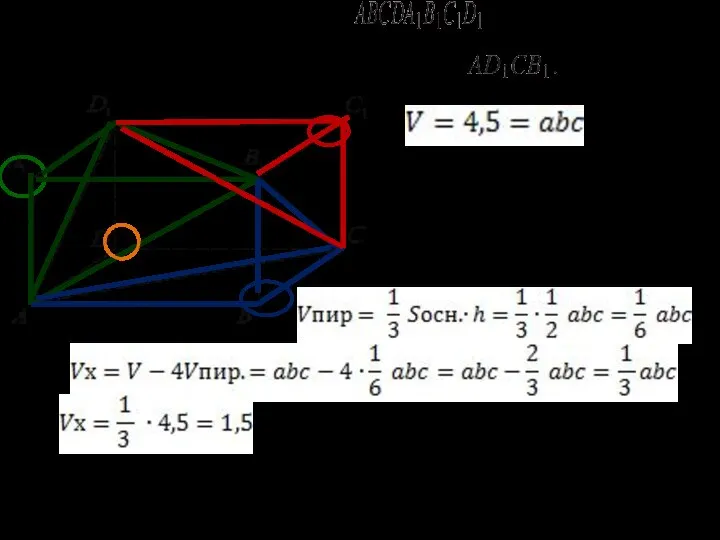
- 19. 14. Объем параллелепипеда равен 4,5. Найдите объем треугольной пирамиды Ответ: 1,5.
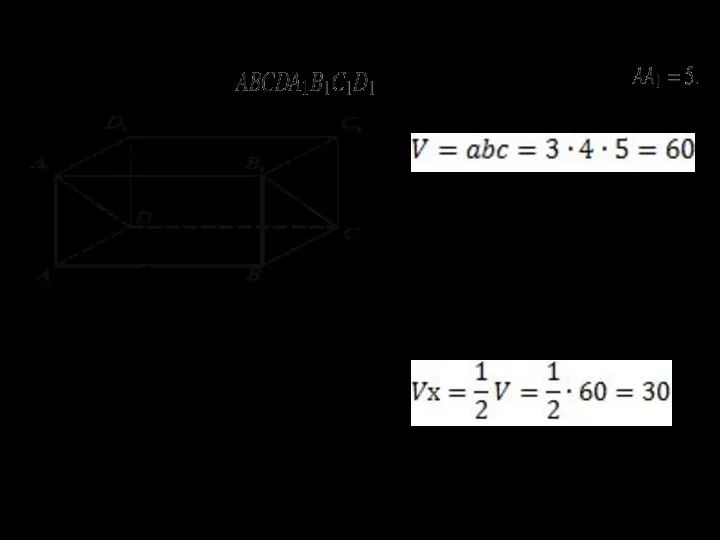
- 20. 15. Найдите объем многогранника, вершинами которого являются точки A, D, A1, B, C, B1 прямоугольного параллелепипеда
- 21. 16. Найдите объем многогранника, вершинами которого являются точки A , B ,C , прямоугольного параллелепипеда ,
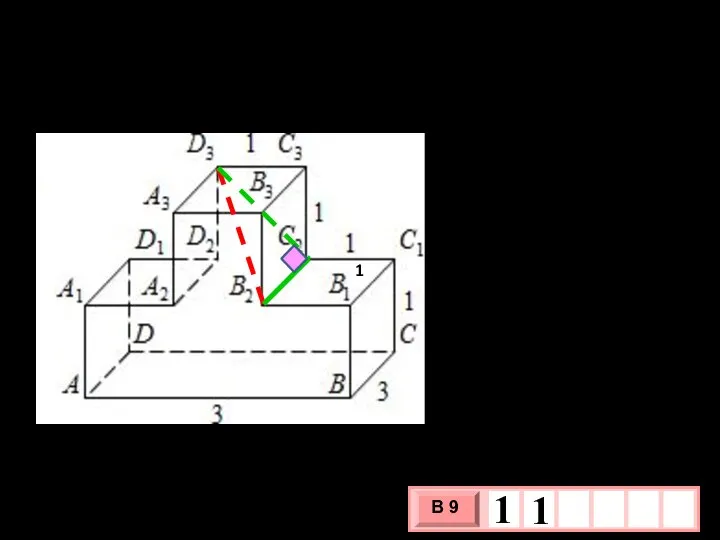
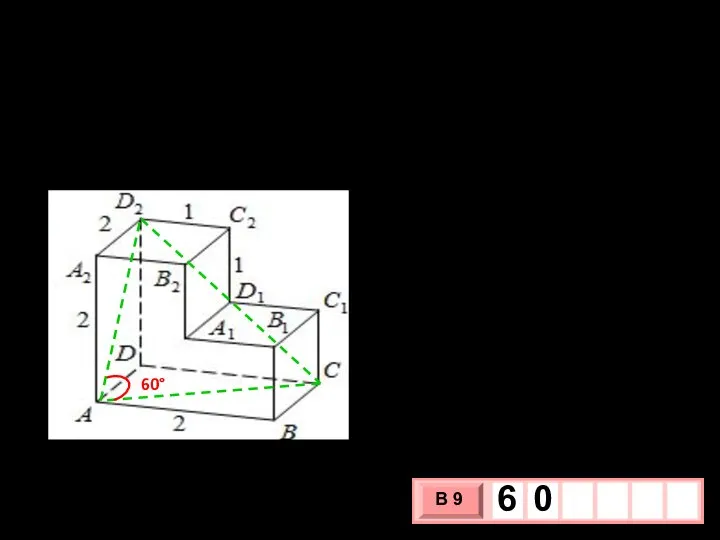
- 22. №5. ОБЗ ЕГЭ №245376. Найдите квадрат расстояния между вершинами B₂ и D ₃ многогранника , изображенного
- 23. № 6. ОБЗ ЕГЭ №245373. Найдите угол CAD₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника
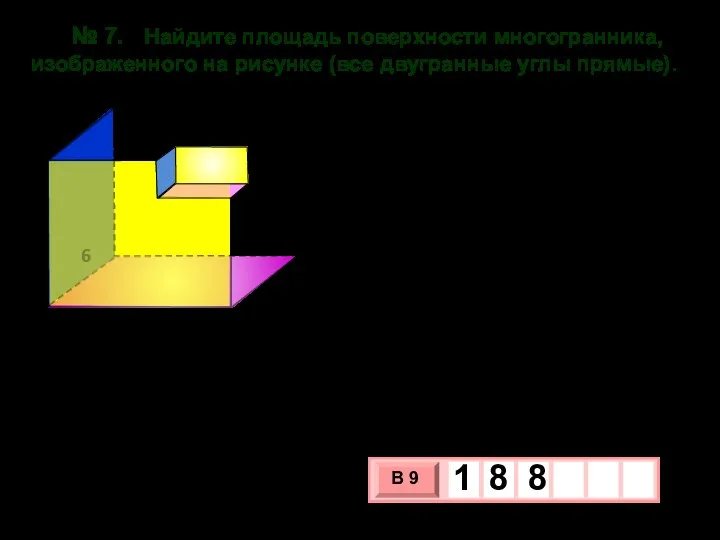
- 24. № 7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Площадь поверхности данной
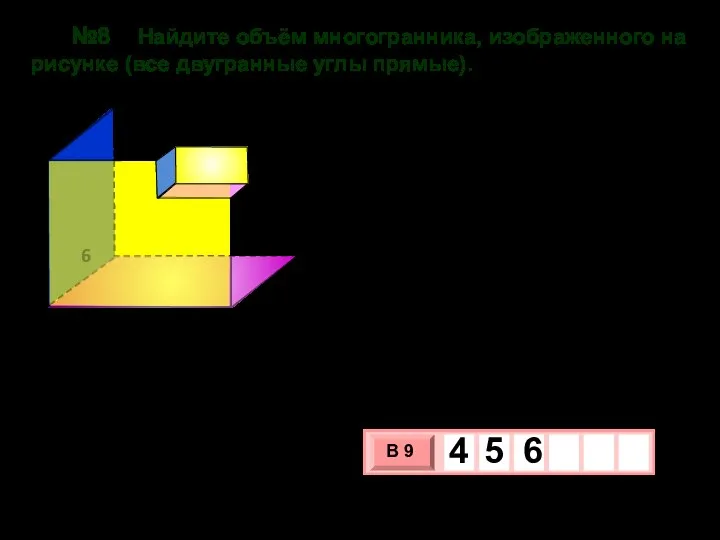
- 25. №8. Найдите объём многогранника, изображенного на рисунке (все двугранные углы прямые). 6 4 3 2 10
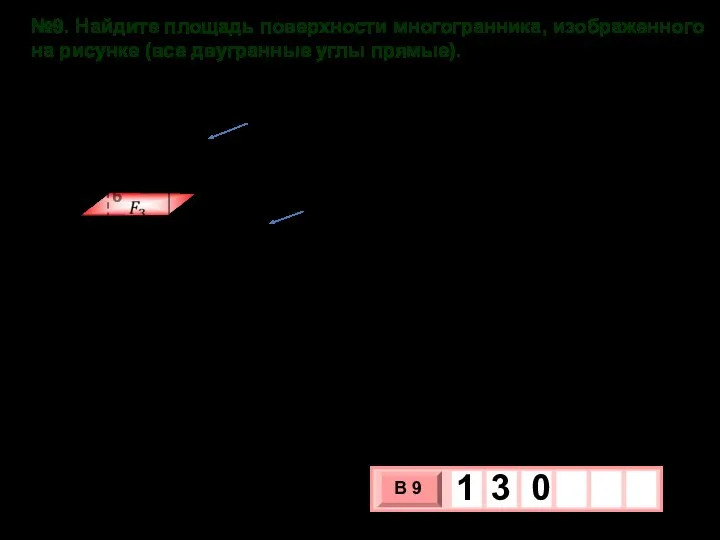
- 26. №9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 2 3 4 6
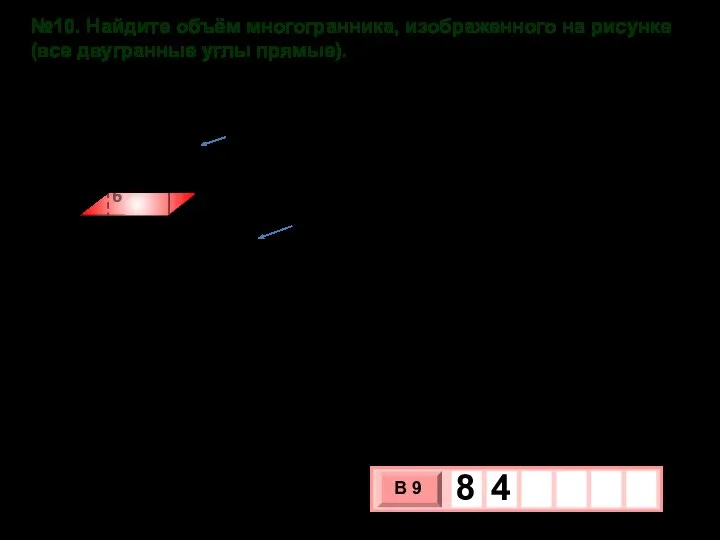
- 27. №10. Найдите объём многогранника, изображенного на рисунке (все двугранные углы прямые). 2 3 4 6 4
- 29. Скачать презентацию









 Меры длины
Меры длины Сложение и вычитание многочленов
Сложение и вычитание многочленов Заморочки из бочки. Урок-игра Счастливый случай
Заморочки из бочки. Урок-игра Счастливый случай Презентация на тему Правильные многогранники и их построение
Презентация на тему Правильные многогранники и их построение  Дисперсионный анализ
Дисперсионный анализ Вписанный угол
Вписанный угол Сложение и вычитание обыкновенных дробей. Графический диктант
Сложение и вычитание обыкновенных дробей. Графический диктант Презентация по математике "Перестановка слагаемых" -
Презентация по математике "Перестановка слагаемых" -  Внутри, вне, на границе
Внутри, вне, на границе Обратные тригонометрические функции
Обратные тригонометрические функции Решение заданий
Решение заданий Вычисления с многозначными числами
Вычисления с многозначными числами Презентация на тему Целое и части (1 класс)
Презентация на тему Целое и части (1 класс)  Квадратные уравнения
Квадратные уравнения Особенности проведения олимпиады по математике в 2016-17 учебном году
Особенности проведения олимпиады по математике в 2016-17 учебном году Структура. Определение
Структура. Определение Контрольная работа
Контрольная работа Умножение на 2 и 3. Закрепление
Умножение на 2 и 3. Закрепление Все действия с десятичными дробями
Все действия с десятичными дробями Презентация на тему ГРАФИК ДВИЖЕНИЯ
Презентация на тему ГРАФИК ДВИЖЕНИЯ  Векторная алгебра
Векторная алгебра chislo-pi
chislo-pi Обыкновенные дроби
Обыкновенные дроби Презентация на тему Единицы площади (4 класс)
Презентация на тему Единицы площади (4 класс)  Сантиметр. Линейка
Сантиметр. Линейка Прямоугольник. Признак прямоугольника
Прямоугольник. Признак прямоугольника Первообразная
Первообразная Прямоугольник
Прямоугольник