Содержание
- 2. Признак делимости на 2 Для того чтобы натуральное число делилось на 2, необходимо и достаточно, чтобы
- 3. Признак делимости на 5 Для того чтобы натуральное число делилось на 5, необходимо и достаточно, чтобы
- 4. Признак делимости на 10 Для того чтобы натуральное число делилось на 10, необходимо и достаточно, чтобы
- 5. Признак делимости на 3 Для того чтобы натуральное число делилось на 3, необходимо и достаточно, чтобы
- 6. Признак делимости на 9 Для того чтобы натуральное число делилось на 9, необходимо и достаточно, чтобы
- 7. Признак делимости на 4 Для того чтобы натуральное число p, содержащее не менее трёх цифр, делилось
- 8. Признак делимости на 8 Для того чтобы натуральное число p, содержащее не менее четырёх цифр, делилось
- 9. Признак делимости на 25 Для того чтобы натуральное число p, содержащее не менее трёх цифр, делилось
- 10. Признак делимости на 125 Для того чтобы натуральное число p, содержащее не менее четырёх цифр, делилось
- 11. Признак делимости на 7 (на 13) Для того чтобы натуральное число делилось на 7 (на 13),
- 13. Скачать презентацию










 Презентация на тему Прямоугольные треугольники
Презентация на тему Прямоугольные треугольники  Алгоритм решения комбинаторных задач
Алгоритм решения комбинаторных задач Алгебра логики
Алгебра логики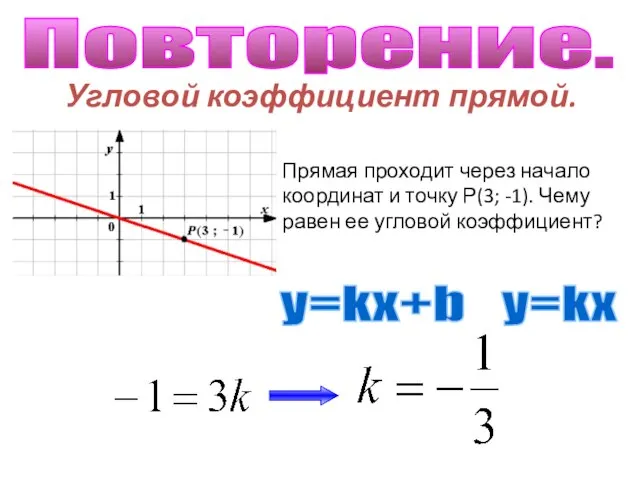 Угловой коэффициент прямой.
Угловой коэффициент прямой. Бесконечность
Бесконечность Презентация на тему Построение диаграмм и графиков функций
Презентация на тему Построение диаграмм и графиков функций  matematika_6_kl_04_10
matematika_6_kl_04_10 РўР’РёРњРЎ_Лекция 5_Непрерывные СЃРучайные РІРµРичины
РўР’РёРњРЎ_Лекция 5_Непрерывные СЃРучайные РІРµРичины Движение
Движение Презентация
Презентация Перпендикулярні площини. Практика 1
Перпендикулярні площини. Практика 1 Ребусы. Алгебра
Ребусы. Алгебра Производная, монотонность, экстремумы
Производная, монотонность, экстремумы Взаимно обратные числа
Взаимно обратные числа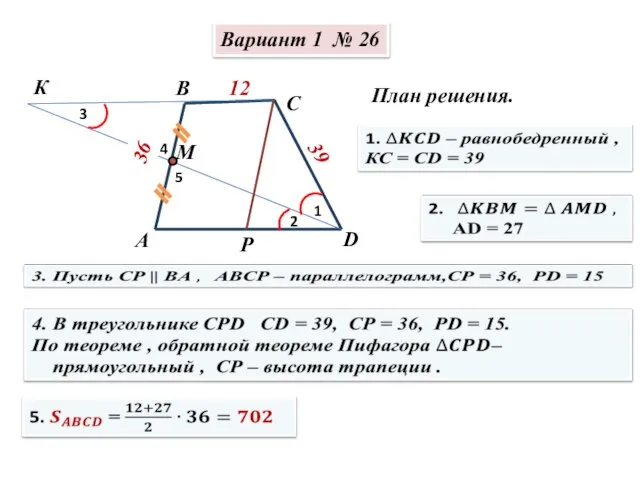 Сборник И.В. Ященко. Решение заданий №26
Сборник И.В. Ященко. Решение заданий №26 Волшебная страна - Геометрия
Волшебная страна - Геометрия Треугольники. Часть 1
Треугольники. Часть 1 Первообразная. Таблица первообразных
Первообразная. Таблица первообразных Начальные геометрические сведения. Параллельные прямые
Начальные геометрические сведения. Параллельные прямые Внеаудиторная самостоятельная работа по теме: Функция, ее свойства и график
Внеаудиторная самостоятельная работа по теме: Функция, ее свойства и график Математика вокруг нас узоры и орнаменты на посуде
Математика вокруг нас узоры и орнаменты на посуде Дифференцирование оригинала, интегрирование оригинала, дифференцирование изображения, интегрирование изображения
Дифференцирование оригинала, интегрирование оригинала, дифференцирование изображения, интегрирование изображения Решение задач на проценты. Урок - сказка
Решение задач на проценты. Урок - сказка Задачи на движение
Задачи на движение GANشبکه های
GANشبکه های Гарри Поттер и теория вероятностей или как найти вероятность победы Гарри Поттера над Волан-де-Мортом
Гарри Поттер и теория вероятностей или как найти вероятность победы Гарри Поттера над Волан-де-Мортом Логарифмы и их свойства
Логарифмы и их свойства Своя игра (2)
Своя игра (2)