Содержание
- 2. Понятие вектора. Равенство векторов. Какова разница между векторными и скалярными величинами? Векторными величинами называют величины, имеющие
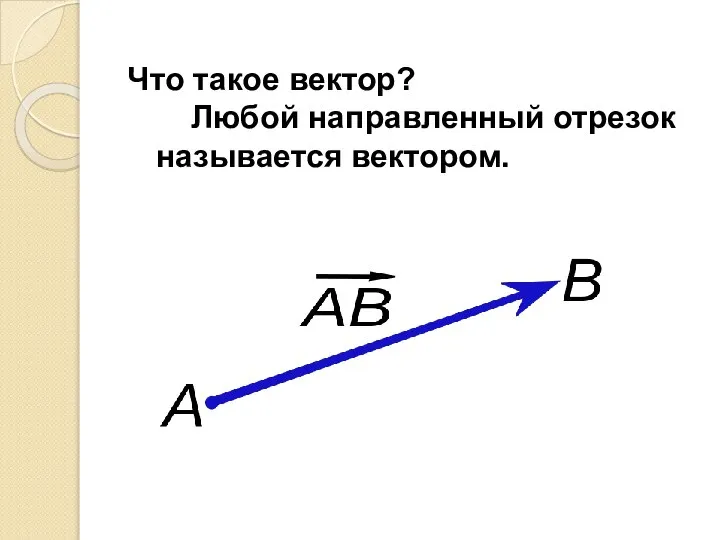
- 3. Что такое вектор? Любой направленный отрезок называется вектором.
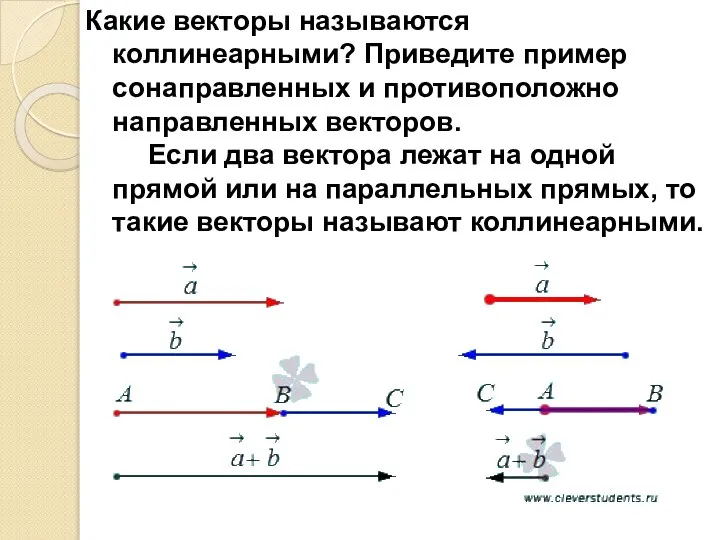
- 4. Какие векторы называются коллинеарными? Приведите пример сонаправленных и противоположно направленных векторов. Если два вектора лежат на
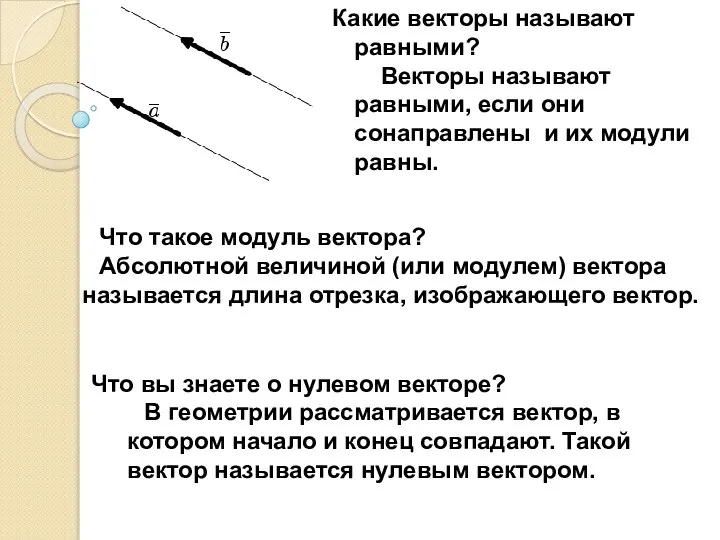
- 5. Что такое модуль вектора? Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Какие векторы
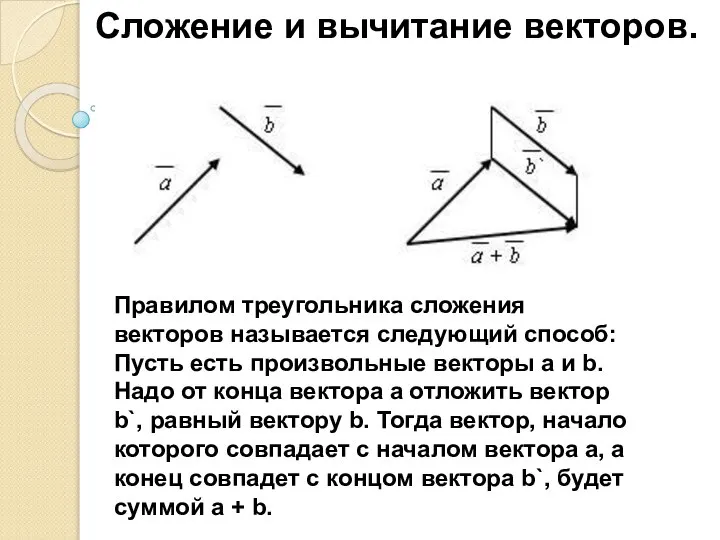
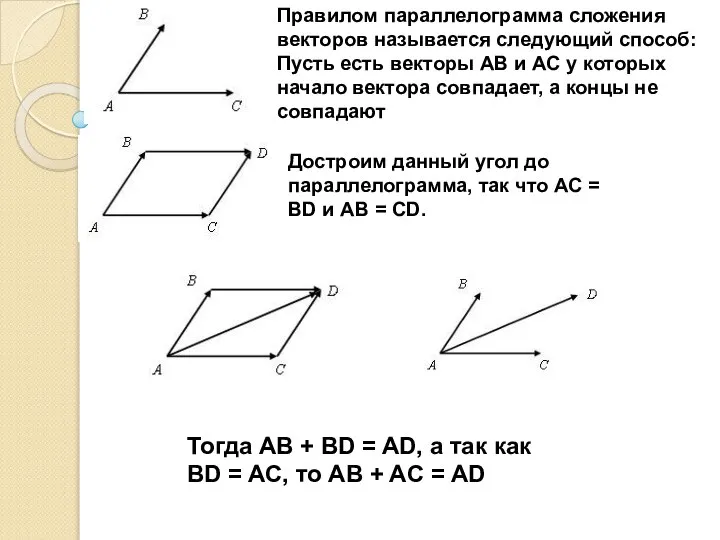
- 6. Сложение и вычитание векторов. Правилом параллелограмма сложения векторов называется следующий способ: Пусть есть векторы AB и
- 7. Правилом параллелограмма сложения векторов называется следующий способ: Пусть есть векторы AB и AC у которых начало
- 8. Противоположным данному называется вектор, начало которого совпадает с концом данного, а конец с началом данного (такой,
- 9. Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла
- 10. Раздел математики, изучающий векторы и действие над ними называется векторной алгеброй. Аппарат векторной алгебры удобен при
- 11. Любой вектор можно разложить по двум произвольным неколлинеарным векторам. Если на плоскости выбраны два таких вектора,
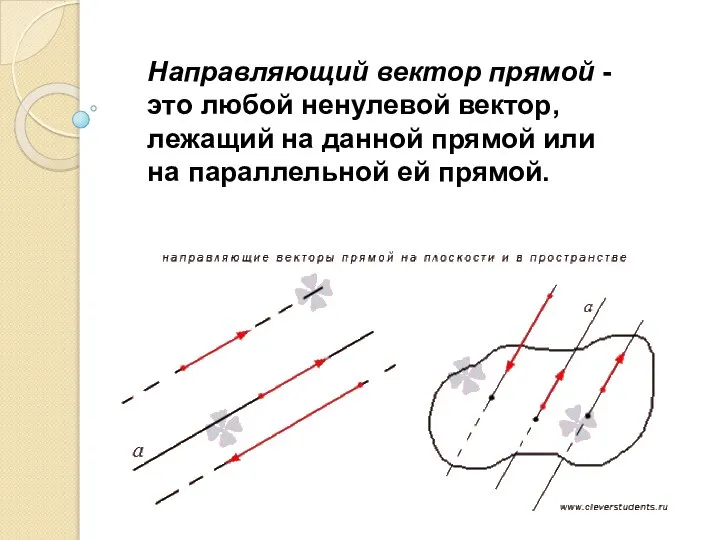
- 12. Направляющий вектор прямой - это любой ненулевой вектор, лежащий на данной прямой или на параллельной ей
- 14. Скачать презентацию





 Математика в профессии сварщика
Математика в профессии сварщика Теория вероятностей. Действия над вероятностями
Теория вероятностей. Действия над вероятностями Числовые и буквенные выражения
Числовые и буквенные выражения ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА Измерение объема жидких и сыпучих веществ с помощью условной меры масс
Измерение объема жидких и сыпучих веществ с помощью условной меры масс Интерактивный пазл
Интерактивный пазл Среднее арифметическое
Среднее арифметическое Производная сложной функции
Производная сложной функции Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Построение графиков функций при помощи геометрических преобразований
Построение графиков функций при помощи геометрических преобразований Математика в лицах.11б
Математика в лицах.11б Теория вероятностей
Теория вероятностей Стандартный вид одночлена
Стандартный вид одночлена Когда выполнение одного условия обеспечивает выполнение другого
Когда выполнение одного условия обеспечивает выполнение другого Виды неопределенностей и методы их разрешения
Виды неопределенностей и методы их разрешения Тренажёр. Таблица умножения. Юные водители
Тренажёр. Таблица умножения. Юные водители Частные производные второго порядка. Первый и второй дифференциалы. Локальный экстремум
Частные производные второго порядка. Первый и второй дифференциалы. Локальный экстремум Математика. Составные высказывания
Математика. Составные высказывания Математика. 3 класс
Математика. 3 класс Справедливость равенства. Устный счет
Справедливость равенства. Устный счет Понятие десятичной дроби
Понятие десятичной дроби Разложение вектора по трем некомпланарным векторам
Разложение вектора по трем некомпланарным векторам Весёлая математика. А ну-ка посчитай
Весёлая математика. А ну-ка посчитай Векторный анализ -теория поля. Типы векторных полей. Лекция 18
Векторный анализ -теория поля. Типы векторных полей. Лекция 18 Математический анализ. Исследование функций и построение графиков. Асимптоты графика функции
Математический анализ. Исследование функций и построение графиков. Асимптоты графика функции Кривая Коха. Дробная размерность. Метод L-систем
Кривая Коха. Дробная размерность. Метод L-систем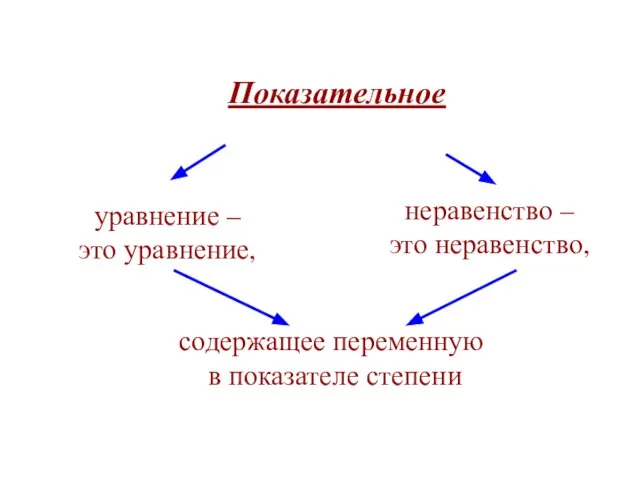 Показательное уравнение
Показательное уравнение Пифагор и его теорема
Пифагор и его теорема