Пирамида. Творческая групповая работа 11класс

Пирамиды в нашей жизни. (Хакимзянова О.,Алёхин Д.,Охотин К.)
Теория.(Лебедев В., Маркелов Ж., Новосёлова Л.)
Применение теории в задачах. (Коротких К., Лыткин К., Самсоненко М.)
План работы

До наших дней дошли только некоторые пирамиды. Остальные погибли из-за
землетрясений, пожаров и вражеских нашествий. Большая пирамида Хеопса
была построена в 4-3 тысячелетий до н. э. Потребовалось 100000 человек, что бы
за 20 лет водрузить один на другой 2300000 каменных блоков, каждый из которых
в среднем весил 2 тонны. Чтобы поставить на место один блок, нужны были
усилия 40 человек. Древние египтяне производили измерения с помощью веревки
с завязанными на ней узелками. Их измерения были очень точными – ошибка
составляла не белее 1,27 см. Сравните эту цифру с высотой пирамиды – 146
метров! Обычно мы связываем пирамиды с древним Египтом. Удивительно, но
самая большая пирамида расположена в Мексике. Она повещена богу Кетцаль-
коатлю и построена 100 лет н. э. Пирамида построена из высушенных на солнце
кирпичей и земли. Хотя высота ее «всего» 53,9 метра, зато площадь 18,2 га.
Экосистемы очень разнообразны по относительной скорости создания и расцвета-
ния, как чистой первичной продукции,так и чистой вторичной продукции на каждом
графическом уровне.Однако всем без исчисления экосистемой свойственны опре-
деления количественные соотношения первичной и вторичной продукции. Правило
пирамиды продукции основано на расщеплении энергии в пищевых целях.
Египетские пирамиды
Пирамиды продукции

Великую пирамиду Хефрена стережёт огромное таинственное существо - Сфинкс:
гигант 20 м высотой и 57 м длинной. Странная фигура - лев с человеческой голо-
вой,улыбаясь, смотрит уже 5 000 лет в даль, будто подтверждает старую арабскую
пословицу:«Все обиться времени, но время бояться пирамид».Через века за сфи-
нксом тянется шлейф загадок. Что означает это изображение: портрет Осилиса или
меживой знак между земной жизнью и вечностью? Откуда явился он на египетскую
землю - с территории нынешней Сирии, Эфиопии, из загадочных глубин Южной
Азии? Почему он оказался столь жизнестойким не только в своей каменной ипос-
таси, но и как духовное начало? В мифологии Древний Греции устами сфинкса
изрекались удивительные загадки, во времена Возрождения его улыбку увекове-
чил великий Леонардо да Винчи.
Пирамида биомасс. Если сложить вместе все деревья, кустарники и травы, то они
в сумме будут весить больше чем все травоядные животные, а те больше чем все
охотящиеся на них хищники -получается пищевая пирамида. В её основания лежат
фотосинтезирующие организмы их больше всего, а на самой вершине хищники их
меньше всего.
ПИРАМИДА ХЕФРЕНА
Пищевая пирамида

Пирамидой называется многогранник, который состоит из плоского многоугольника
— основания пирамиды, точки, не лежащей в плоскости основания,— вершины
пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются
боковыми ребрами.
Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая
грань — треугольник. Одной из его вершин является вершина пирамиды, а проти-
волежащей стороной — сторона основания пирамиды.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды
на плоскость основания.
Пирамида называется n-угольной, если ее основанием является n-угольник. Тре-
угольная пирамида называется также тетраэдром.У пирамиды, основание —
многоугольник А1А2...Аn, вершина пирамиды — S, боковые ребра — SA1SA2,...,
SAn, боковые грани — ΔSA1A2,Δ SA2A3,... .
В дальнейшем мы будем рассматривать только пирамиды с выпуклым многоуголь-
ником в основании. Такие пирамиды являются выпуклыми многогранниками.
ПИРАМИДА

ОБЪЕМ
Пусть SABC — треугольная пирамида с вершиной S и основанием ABC. Допол-
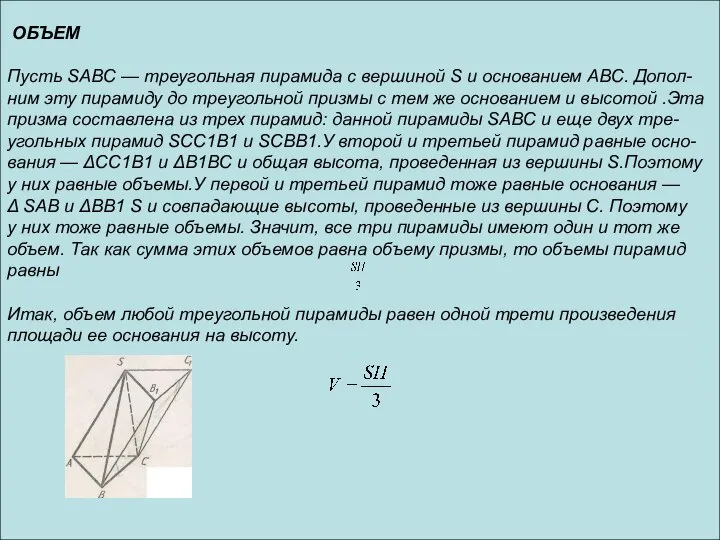
ним эту пирамиду до треугольной призмы с тем же основанием и высотой .Эта
призма составлена из трех пирамид: данной пирамиды SABC и еще двух тре-
угольных пирамид SCC1B1 и SCBB1.У второй и третьей пирамид равные осно-
вания — ΔCC1B1 и ΔB1BC и общая высота, проведенная из вершины S.Поэтому
у них равные объемы.У первой и третьей пирамид тоже равные основания —
Δ SAB и ΔBB1 S и совпадающие высоты, проведенные из вершины С. Поэтому
у них тоже равные объемы. Значит, все три пирамиды имеют один и тот же
объем. Так как сумма этих объемов равна объему призмы, то объемы пирамид
равны
Итак, объем любой треугольной пирамиды равен одной трети произведения
площади ее основания на высоту.
ОБЪЕМ
Пусть SABC — треугольная пирамида с вершиной S и основанием ABC. Допол-
ним эту пирамиду до треугольной призмы с тем же основанием и высотой .Эта
призма составлена из трех пирамид: данной пирамиды SABC и еще двух тре-
угольных пирамид SCC1B1 и SCBB1.У второй и третьей пирамид равные осно-
вания — ΔCC1B1 и ΔB1BC и общая высота, проведенная из вершины S.Поэтому
у них равные объемы.У первой и третьей пирамид тоже равные основания —
Δ SAB и ΔBB1 S и совпадающие высоты, проведенные из вершины С. Поэтому
у них тоже равные объемы. Значит, все три пирамиды имеют один и тот же
объем. Так как сумма этих объемов равна объему призмы, то объемы пирамид
равны
Итак, объем любой треугольной пирамиды равен одной трети произведения
площади ее основания на высоту.

Пусть теперь имеем любую,не обязательно треугольную пирамиду. Разобьем ее
основание на треугольники Δ1, Δ2,… Δ n. Пирамиды, у которых основаниями явля-
ются эти треугольники, а вершинами — вершина данной пирамиды, составляют
данную пирамиду. Объем данной пирамиды равен сумме объёмов составляющих
ее пирамид. Так как все они имеют ту же высоту Н, что и данная пирамида, то
объём ее равен;
Итак, объем любой пирамиды равен одной трети произведения
площади ее основания на высоту.