Содержание
- 2. Линейные неравенства Неравенство вида ах+в≥0, где а, в - любые числа, а≠0, называется линейным. Например: а)
- 3. Что называется решением неравенства? Какие из чисел являются решением неравенства 2х+5 5 7 -1 Х =
- 4. Свойства неравенств: 1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным
- 5. 2. Обе части неравенства можно умножить или разделить на одно и то же положительное число не
- 6. 3. Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив
- 7. Применив свойства неравенства, найдите общее решение 2х+5 2х+5 2х 2х х \\\\\\\\\ Ответ: (-∞; 1) 1
- 8. Решаем у доски: № 1.2(а,б), 1.3 (а,в), 1.4(а,б)
- 9. Дополнительное задание:
- 10. Софизм
- 12. Скачать презентацию








 Задачи на движение в одном направлении из одной точки
Задачи на движение в одном направлении из одной точки Матрицы и действия над ними
Матрицы и действия над ними Разложение многочлена на множители
Разложение многочлена на множители Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы Тригонометрические уравнения и математические термины на английском языке
Тригонометрические уравнения и математические термины на английском языке Определители второго и третьего порядка
Определители второго и третьего порядка Решение систем уравнений с двумя переменными методом подстановки
Решение систем уравнений с двумя переменными методом подстановки Правильные многоугольники
Правильные многоугольники Основы анализа данных. Корреляционный анализ. (Лекция 5)
Основы анализа данных. Корреляционный анализ. (Лекция 5) Презентация на тему Число и цифра 7 (1 класс)
Презентация на тему Число и цифра 7 (1 класс)  Интерактивный тренажер. Числа от 1 до 1000. Нумерация (3 класс)
Интерактивный тренажер. Числа от 1 до 1000. Нумерация (3 класс) Презентация на тему Первый признак равенства треугольников
Презентация на тему Первый признак равенства треугольников  Время и работа. Связь между величинами
Время и работа. Связь между величинами Построение 3 видов группы геометрических тел
Построение 3 видов группы геометрических тел Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Прямоугольный параллепипед. Итоговое повторение
Прямоугольный параллепипед. Итоговое повторение Признаки параллелограмма. 8 класс
Признаки параллелограмма. 8 класс Знакочередующиеся и знакопеременные ряды
Знакочередующиеся и знакопеременные ряды Величины. Объём
Величины. Объём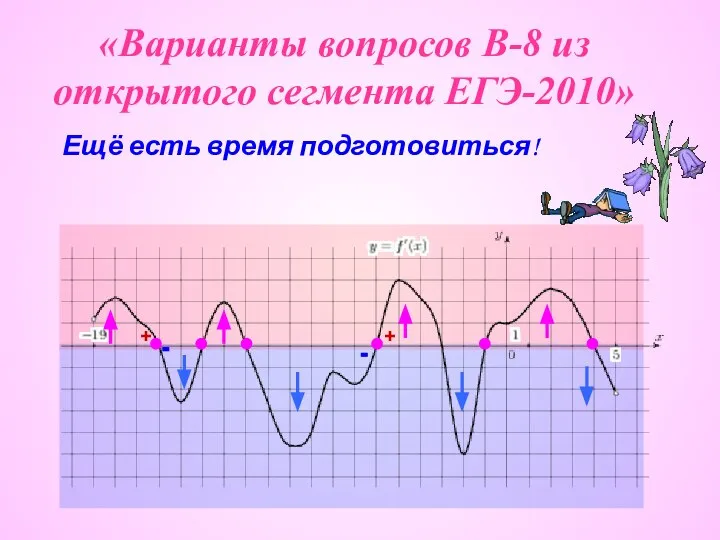 Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Задачи на кратное сравнение
Задачи на кратное сравнение Entrant
Entrant Решение задач (1 класс)
Решение задач (1 класс) Касательная плоскость к сфере
Касательная плоскость к сфере Наука Метрология
Наука Метрология Задача з піцою
Задача з піцою Тригонометрические уравнения
Тригонометрические уравнения Вычисление логарифмов
Вычисление логарифмов