Содержание
- 2. ОДУ высших порядков Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной
- 3. Некоторые типы уравнений, допускающие понижение порядка Уравнение вида решается последовательным n-кратным интегрированием. Пример:
- 4. Переобозначив постоянные, общее решение можно записать в виде : y = sinx + C1x3 + C2x2
- 5. Порядок уравнения вида F(x, y(k), y(k+1), y(k+2), …,y(n)) = 0, не содержащего функции y(x) и (k
- 6. Пример: Понизить порядок уравнения: Младшая производная, входящая в явной форме в уравнение, - вторая, поэтому делаем
- 7. Определение: где a, b и c - постоянные величины. Линейным однородным дифференциальным уравнением второго порядка с
- 8. Для нахождения общего решения данного уравнения составляется характеристическое уравнение: Это уравнение получается из первоначального уравнения (А)
- 9. Общее решение дифференциального уравнения строится в зависимости от характера корней характеристического уравнения Возможны три случая :
- 10. II случай: - действительные и равные, тогда общее решение примет вид: (2) III случай: и -
- 12. Скачать презентацию









 Решение задач. Диагностика 1
Решение задач. Диагностика 1 Математический диктант. 6 класс
Математический диктант. 6 класс Числовые ряды
Числовые ряды Соотношение числа и цифры. Считаем от 1 до 9
Соотношение числа и цифры. Считаем от 1 до 9 Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма
Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма Повторим правила образования и записи чисел
Повторим правила образования и записи чисел Диофантово уравнение
Диофантово уравнение Векторы
Векторы Задачі_на_наслідки_із_аксіом_стереометрії
Задачі_на_наслідки_із_аксіом_стереометрії Числовые головоломки
Числовые головоломки 6cc84cfba09801fa77f2178065bede8f
6cc84cfba09801fa77f2178065bede8f Методы оптимизации. Ограничения в виде равенств и неравенств
Методы оптимизации. Ограничения в виде равенств и неравенств Наибольший общий делитель (НОД) и наименьшее общее кратное чисел (НОК)
Наибольший общий делитель (НОД) и наименьшее общее кратное чисел (НОК) Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка
Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка Regresní a korelační analýza
Regresní a korelační analýza Предел функции (часть 2)
Предел функции (часть 2)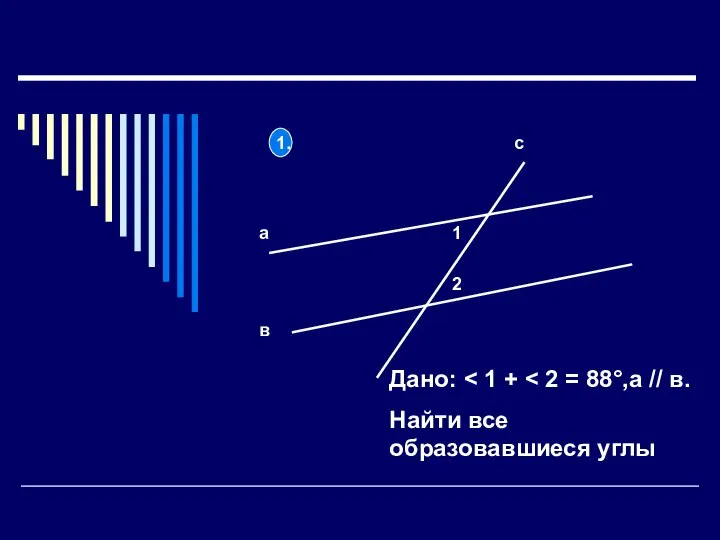 Признаки равенства треугольников
Признаки равенства треугольников Угол между прямой и плоскостью. Теорема о трёх перпендикулярах
Угол между прямой и плоскостью. Теорема о трёх перпендикулярах Подготовка к ЕГЭ (профильный уровень). Задания 5
Подготовка к ЕГЭ (профильный уровень). Задания 5 Уравнения и неравенства в целых числах
Уравнения и неравенства в целых числах Теорема Виета. Устная работа
Теорема Виета. Устная работа Минимизация переключательных функций
Минимизация переключательных функций Прямая и плоскость в пространстве. Лекция 6
Прямая и плоскость в пространстве. Лекция 6 Таблица умножения девяти. Тренажёр-раскраска
Таблица умножения девяти. Тренажёр-раскраска Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Методика изучения одномерных геометрических фигур в курсе математики начальных классов: точка, линия, прямая
Методика изучения одномерных геометрических фигур в курсе математики начальных классов: точка, линия, прямая Диаграммы Ламерея. Качественный анализ дискретных ДС
Диаграммы Ламерея. Качественный анализ дискретных ДС Сложение десятичных дробей
Сложение десятичных дробей