Содержание
- 2. Obictivele lecţiei O1. Să identificăţi formulele de calcul penru aria paralelogramului şi a rombului; O2.Să aplice
- 3. Tehnologii didactice: Metode și procedee: expunerea, explicația, conversația, exercițiul. Forme de organizare:frontală,individuală Mijloace de învățământ: Manual
- 4. Unitatea principală de măsură pentru suprafeţe este metrul pătrat.
- 5. Aria pătratului Aria pătratului este egală cu lungimea laturii la pătrat. A = l2 l l
- 6. Aria dreptunghiului Aria dreptunghiului este egală cu produsul dintre lungime şi lăţime. A = L ∙
- 7. Aria triunghiului oarecare Aria unui triunghi este egală cu jumătate din produsul unei laturi cu înălţimea
- 8. Aria triunghiului dreptunghic Aria triunghiului dreptunghic este egală cu jumătate din produsul dintre ipotenuză şi înălţimea
- 9. Aria paralelogramului Aria unui paralelogram este egală cu produsul unei laturi cu înălţimea corespunzătoare. A =
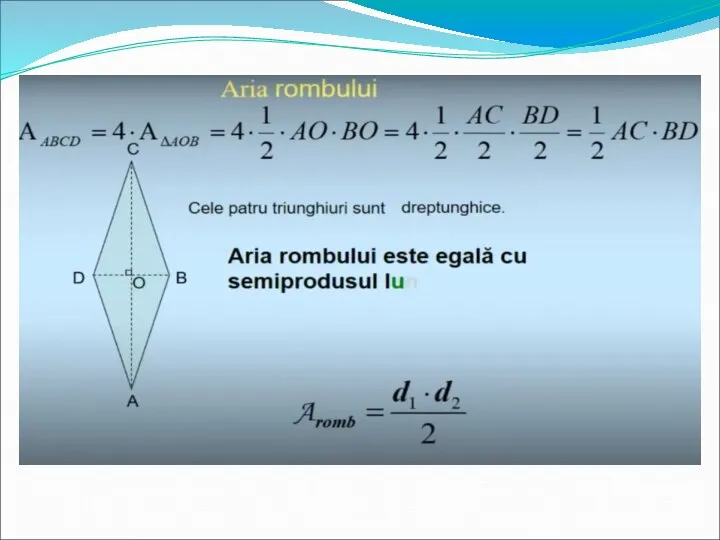
- 10. Aria rombului Aria unui romb este egală cu produsul unei laturi cu înălţimea corespunzătoare. Aria unui
- 17. De ce trebuie sa cunoastem foarte bine notiunuile de arie si perimetru? Pentru a putea rezolva
- 18. O gradina are forma unei suprafete dreptunghiulare cu latimea de 40 m si lungimea de 120
- 19. Să aplicăm formulele! 1. Aria unui dreptunghi cu dimensiunile de 5,7 cm şi 10 cm este
- 20. Temă pentru acasă 1. De repetat formulele de calcul pentru ariile figurilor plane 2.De rezolvat problema
- 21. Să verificăm rezultatele! 1.57 cm2 2.15 cm2 3. 49 cm2 4. cm2 5. 6. 108 cm2
- 22. 1.Calculaţi aria unui pătrat care are perimetrul de 28 cm. 2.Aflaţi aria unui triunghi dreptunghic care
- 23. 6.Care este aria unui romb care are diagonalele de 36 cm şi 48 cm? 7.Calculaţi aria
- 25. Скачать презентацию





















 Презентация по математике "Ломаные числа" -
Презентация по математике "Ломаные числа" -  Пирамида. Развёртка пирамиды
Пирамида. Развёртка пирамиды Составные уравнения
Составные уравнения Нуль без палочки. Математический турнир
Нуль без палочки. Математический турнир Ккомбинаторика. Перестановки. Размещения. Сочетания
Ккомбинаторика. Перестановки. Размещения. Сочетания Прикладная математика. Лекция 10. Контрольная работа
Прикладная математика. Лекция 10. Контрольная работа Rinjka liinija
Rinjka liinija Разложение вектора по базису
Разложение вектора по базису Геометрия в природе
Геометрия в природе Оснащение математических уголков в ДОУ
Оснащение математических уголков в ДОУ Определение производной. Правила вычисления производных. Таблица производных
Определение производной. Правила вычисления производных. Таблица производных Сложение и вычитание обыкновенных дробей. Графический диктант
Сложение и вычитание обыкновенных дробей. Графический диктант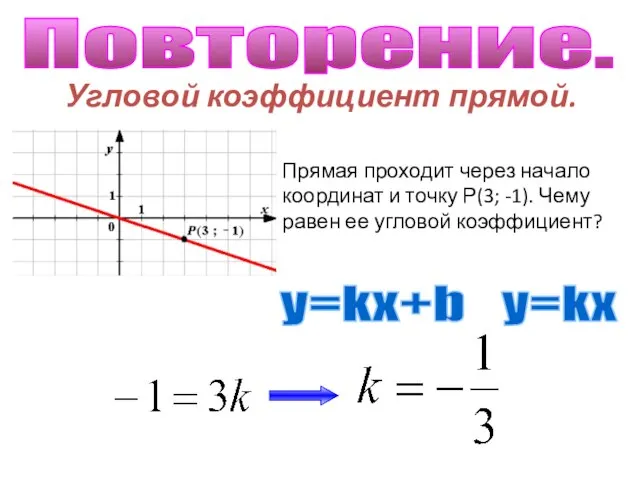 Угловой коэффициент прямой.
Угловой коэффициент прямой. Параллелограм и трапеция
Параллелограм и трапеция Деление многозначных чисел в столбик по программе 4 класса
Деление многозначных чисел в столбик по программе 4 класса Теория вероятностей и математическая статистика (Лекция 5)
Теория вероятностей и математическая статистика (Лекция 5) Связь между величинами: цена, количество, стоимость
Связь между величинами: цена, количество, стоимость Решение систем линейных уравнений методом сложения
Решение систем линейных уравнений методом сложения Трапеция
Трапеция Число 10. Запись числа 10
Число 10. Запись числа 10 Системы счисления
Системы счисления Письмове додавання трицифровий чисел, коли сума одиниць дорівнює 10 або сума десятків дорівнює 10 десяткам. Урок 82
Письмове додавання трицифровий чисел, коли сума одиниць дорівнює 10 або сума десятків дорівнює 10 десяткам. Урок 82 Логарифмы вокруг нас
Логарифмы вокруг нас Как появилась алгебра!
Как появилась алгебра! Производная функции
Производная функции Что такое математика?
Что такое математика? Многочлены от нескольких переменных
Многочлены от нескольких переменных Функция нескольких переменных
Функция нескольких переменных