Содержание
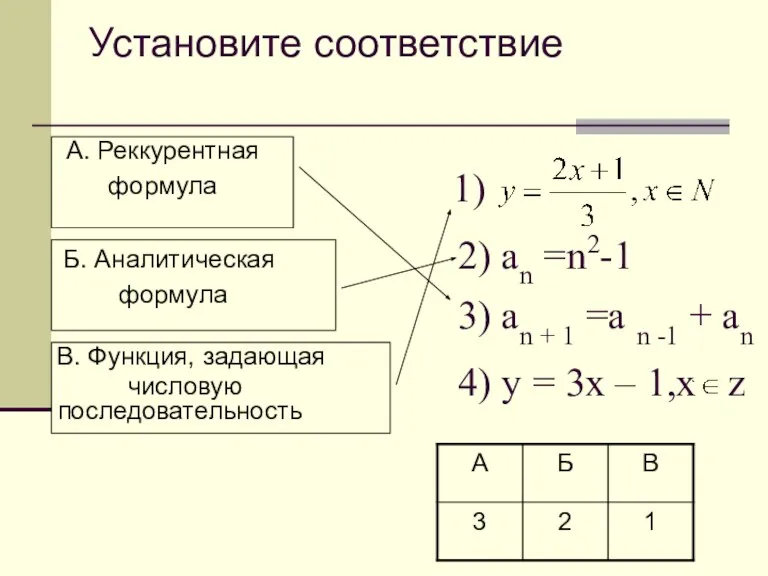
- 2. Установите соответствие А. Реккурентная формула Б. Аналитическая формула В. Функция, задающая числовую последовательность 2) an =n2-1
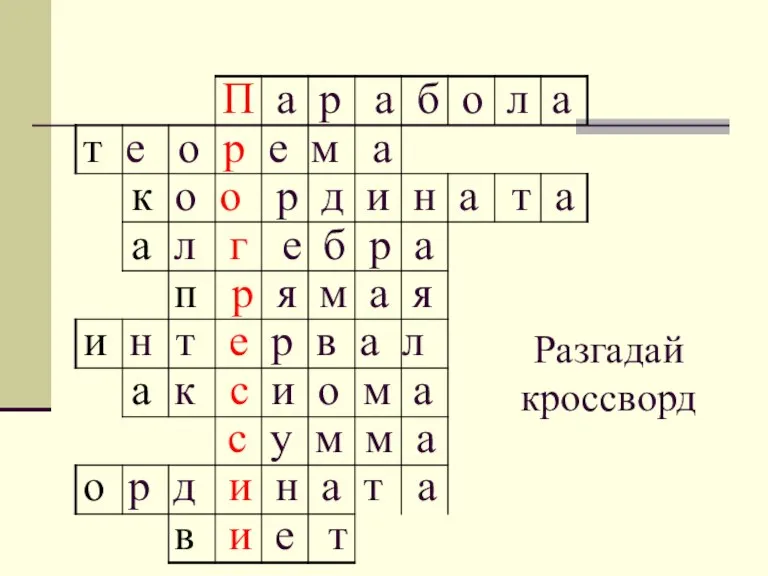
- 3. Разгадай кроссворд П а р а б о л а т е о р е м
- 4. Что такое прогрессия? Термин «прогрессия» имеет латинское происхождение (progression), что означает «движение вперед» и был введен
- 5. Древний Египет Первые представления о прогрессиях были уже у древних народов. В египетских папирусах встречаются задачи
- 6. Карл Гаусс Нашёл моментально сумму всех натуральных чисел от 1 до 100, будучи ещё учеником начальной
- 7. Тема урока: «Арифметическая прогрессия»
- 8. Определение арифметической прогрессии: Арифметическая прогрессия – числовая последовательность, каждый член которой, начиная со второго, равен сумме
- 9. Разность арифметической прогрессии d = an + 1 – an Если d >0, то арифметическая прогрессия
- 10. Задача Курс воздушных ванн начинают с 15 мин в первый день и увеличивают время этой процедуры
- 11. Задача На складе 1 числа было 50 т угля. Каждый день в течение месяца на склад
- 12. Формула n –го члена an = a1 + (n - 1)d
- 13. А знаете ли вы? – стихотворный размер, когда ударение падает на 2 слог. Уж небо осенью
- 14. Задача: В арифметической прогрессии некоторые члены отсутствуют: 3; а2; 7; а4; 11 Можно ли восстановить пропущенные
- 15. Свойства арифметической прогрессии а1; а2; а3; а4;… аn – 1; an; an + 1; … аn
- 16. Проверь себя Продолжить арифметическую прогрессию -3, 0, 3, … В арифметической прогрессии -1; 2; 5; 8;
- 17. Задача Дана стайка чисел из арифметической прогрессии: 3, 5, 7, 9, 11, 13, 15, 17, 19.
- 18. Рефлексия Я узнал … Я для себя открыл … Тем первым, кто находит ход решения задач,
- 20. Скачать презентацию















 Равносильность уравнений. 11 класс
Равносильность уравнений. 11 класс Прогрессии
Прогрессии Кривые второго порядка. Практика
Кривые второго порядка. Практика Эскизы кривых на плоскости, заданных параметрически
Эскизы кривых на плоскости, заданных параметрически Линейная алгебра просто! интерактивное учебное пособие
Линейная алгебра просто! интерактивное учебное пособие Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс Презентация на тему Симметрия. Осевая и центральная симметрии
Презентация на тему Симметрия. Осевая и центральная симметрии  Приведение дробей к общему знаменателю Молодых Наталья Андреевна Учитель математики средней школы № 3 г.Каменска- Уральского Св
Приведение дробей к общему знаменателю Молодых Наталья Андреевна Учитель математики средней школы № 3 г.Каменска- Уральского Св Двугранный угол. Перпендикулярность плоскостей
Двугранный угол. Перпендикулярность плоскостей Математический КВН
Математический КВН Преобразование графиков
Преобразование графиков Величины. Масса (1 класс)
Величины. Масса (1 класс)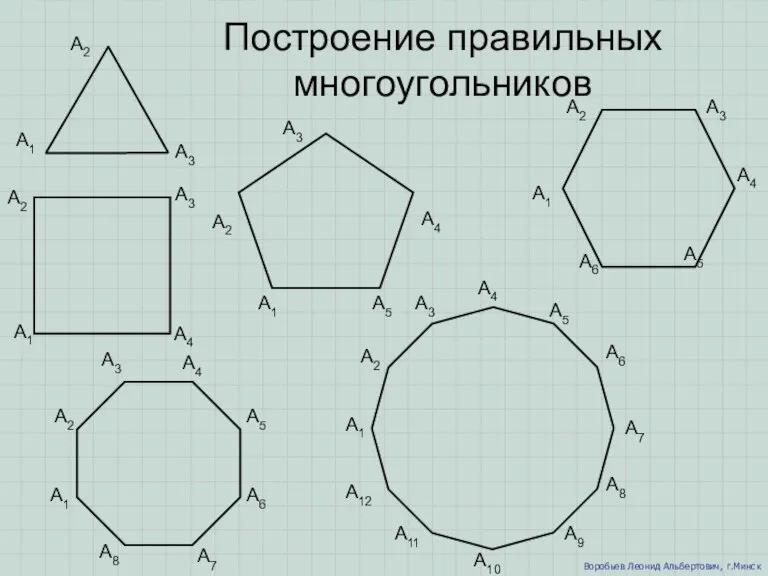 Построение правильных многоугольников
Построение правильных многоугольников Тест 3 по математике
Тест 3 по математике Рисунки из геометрических фигур
Рисунки из геометрических фигур Сравнение, сложение и вычитание дробей с разными знаменателями
Сравнение, сложение и вычитание дробей с разными знаменателями Сборник задач Во имя тех священных дней
Сборник задач Во имя тех священных дней Lek-AFK-Differentsialnye_uravnenia
Lek-AFK-Differentsialnye_uravnenia Геометрический смысл производной f '(x₀) = tg α = к
Геометрический смысл производной f '(x₀) = tg α = к Решение задач
Решение задач Квадратичная функция. Наглядно-методическое пособие. 9 класс
Квадратичная функция. Наглядно-методическое пособие. 9 класс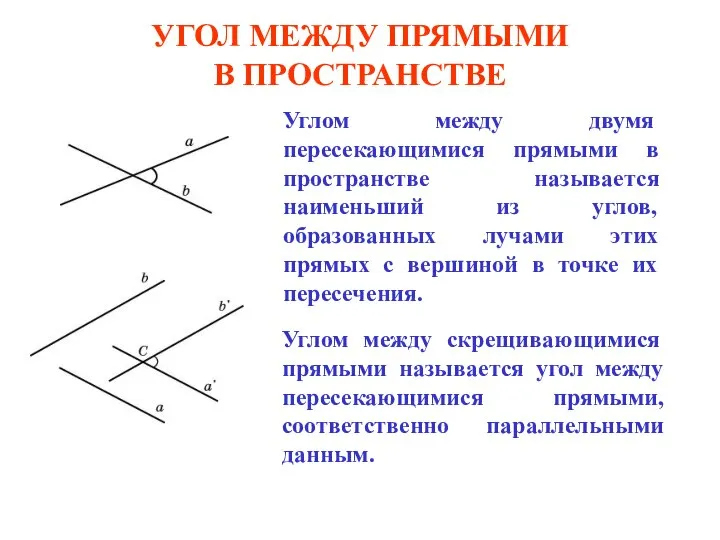 Угол между двумя прямыми в пространстве Вариант 2.ppt
Угол между двумя прямыми в пространстве Вариант 2.ppt Методы кластеризации
Методы кластеризации Без знаний дробей никто не может признаваться знающим арифметику
Без знаний дробей никто не может признаваться знающим арифметику Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ  Интерактивный тренажер Подобные слагаемые
Интерактивный тренажер Подобные слагаемые Площадь фигуры. Сравнение площадей
Площадь фигуры. Сравнение площадей