Слайд 2
Из истории;
Понятие о производной;
Правила вычисления производной: -Основные правила дифференцирования, -Производная степенной

функции.
Производная сложной функции: -Сложная функция, -Производная триногометрических функций;
Применение.
Слайд 3Формула производной встречается нам ещё в 15 веке. Великий итальянский математик Тартальи,

рассматривая и развивая вопрос - на сколько зависит дальность полёта снаряда от наклона орудия - применяет её в своих трудах.
Посвящает целый трактат о роли производной в математике известный учёный Галилео Галилей. Затем производная и различные изложения с её применением стали встречаться в работах Декарта, французского математика Роберваля и англичанина Грегори. Большой вклад по изучению производной внесли такие умы, как Лопиталь, Бернулли, Лангранж и др
Слайд 4Понятие о производной
Производной функции f в точке x0 называется число, к которому

стремится разностное отношение
∆f/Δx=f(x0+Δx)-f(x0)/Δx
при ΔX, стремящемся к нулю.
Слайд 5Основные правила дифференцирования
Правило №1. Если функции u и v дифференцируемы в точке

x0,то их сумма дифференцируема в этой точке (u+v)'= u'+v'.
Коротко говорят: производная суммы равна сумме производных.
Слайд 6Лемма. Если функция f дифференцируема в точке x0,то она непрерывна в этой

точке: ∆f→0 при ∆x→0, т.е.
f(x0+∆x )→(x0) при ∆x→0.
Слайд 7Правило №2. Если функции u и v дифференцируема в точке x0,то произведение

дифференцируемо в этой точке и (uv)'=u'v+uv'.
Слайд 8Следствие.Если функция u дифференцируема в точке x0,а С-постоянная, то функция Cu дифференцируема

в этой точке и (Cu)'=Cu'.
Коротко говорят: постоянный множитель можно выносить за знак производной.
Слайд 9Правило №3. Если функции u и v дифференцируемы в точке x0 и

функция v не равна нулю в этой точке, то частное u/v также дифференцируемо в x0 и
(u/v)'=u'v-uv'/v².
Слайд 10Производная степенной функции:
Для любого целого n и любого x (x≠0 при n≤1)

(xⁿ)'=nxⁿ־¹.
Слайд 11Целые рациональные функции (многочлены) и дробно-рациональные функции дифференцируемы в каждой точке своей

области определения.
Слайд 12Производная сложной функции:
Если функция f имеет производную в точке x0,а функция

g имеет производную в точке y0=f(x0), то сложная функция h(x)=g(f(x)) также имеет производную в точке x0 причём h'(x0)=g'(f(x0))·f '(x0).
Слайд 13Производные тригонометри -
ческих функций:
Формула производной синуса: Функция синус имеет производную в любой

точке и (sin x)'=cos x.
Слайд 14Формулы дифференцирования косинуса, тангенса и котангенса: функции y=cos x, y=tg x, y=ctg

x имеют производные вкаждой точке своей области определения,
и справедливы формулы:
(cos x)'=-sin x,
(tg x)'=1/cos² x,
(ctg x)'=-1/sin²x.
Слайд 15(sin x)'=cos x
(cos x)'=-sin x,
(tgx)'=1/cos² x,
(ctg x)'=-1/sin²x.
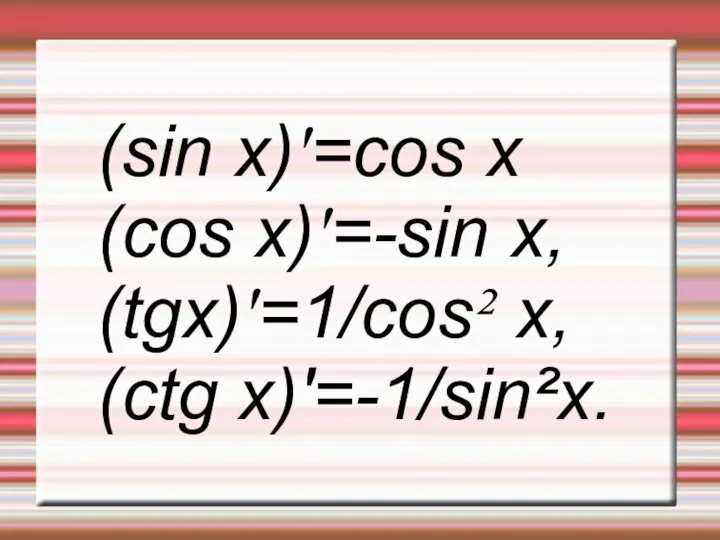
Слайд 16 Производные широко применимы в настоящее время, например, в экономическом анализе. Они

помогают точно вывести данные об изменении экономики государства. Используя их, можно совершенно точно просчитать, как можно увеличить доход государства и за счёт чего он может быть увеличен













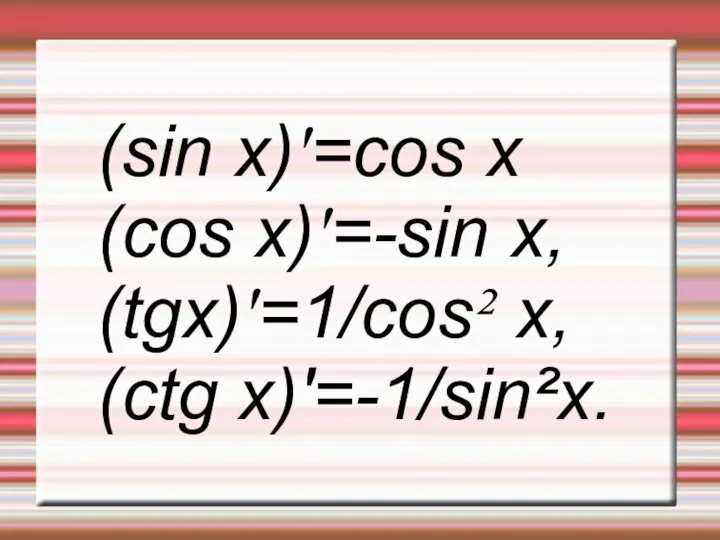

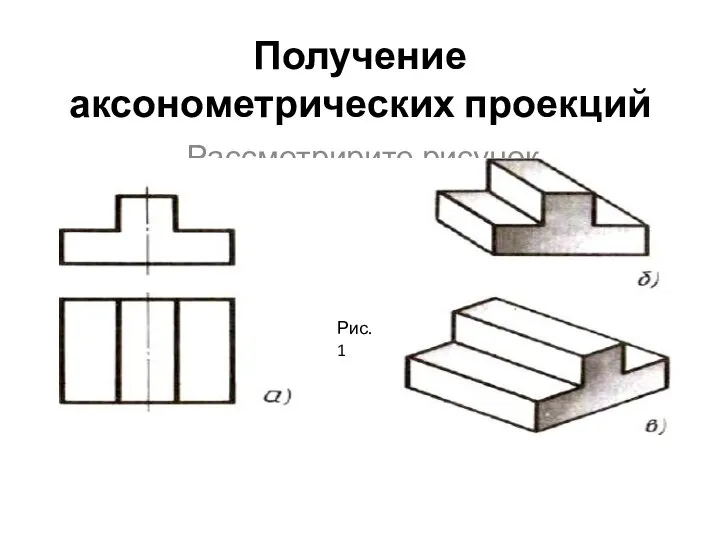 Получение аксонометрических проекций
Получение аксонометрических проекций Тригонометрические уравнения. Методы решения тригонометрических уравнений
Тригонометрические уравнения. Методы решения тригонометрических уравнений Решение задач по теме: Терема Пифагора
Решение задач по теме: Терема Пифагора Презентация на тему Подобные треугольники
Презентация на тему Подобные треугольники  Логика. Логические функции
Логика. Логические функции Наши проекты. Оригами Странички для любознательных
Наши проекты. Оригами Странички для любознательных Квадратичная функция и её график
Квадратичная функция и её график Решение одной задачи, не лишено здравого смысла
Решение одной задачи, не лишено здравого смысла Аттестационная работа. Взаимодействие учебной и исследовательской деятельности на уроках математики
Аттестационная работа. Взаимодействие учебной и исследовательской деятельности на уроках математики Координатная плоскость
Координатная плоскость Арксинус, арккосинус, арктангенс, арккотангенс
Арксинус, арккосинус, арктангенс, арккотангенс Декартовы координаты на плоскости (решение задач)
Декартовы координаты на плоскости (решение задач) Способы задания числовых функций
Способы задания числовых функций Роль геометрии в изобразительном искусстве
Роль геометрии в изобразительном искусстве Движение: скорость, время, расстояние
Движение: скорость, время, расстояние Функция y = x2 и её график
Функция y = x2 и её график Неопределенный интеграл
Неопределенный интеграл Диалектика как методология научного познания
Диалектика как методология научного познания Треугольник и его виды
Треугольник и его виды Порядок действий в выражениях
Порядок действий в выражениях Решение задач по теме Параллельность прямой и плоскости
Решение задач по теме Параллельность прямой и плоскости Презентация на тему Тренажер - Табличное умножение и деление
Презентация на тему Тренажер - Табличное умножение и деление  Построение аксонометрических проекций геометрических фигур и тел
Построение аксонометрических проекций геометрических фигур и тел Дифференциальные уравнения
Дифференциальные уравнения Система линейных уравнений
Система линейных уравнений Цилиндр
Цилиндр Математическое моделирование. Воспроизводимость опытов
Математическое моделирование. Воспроизводимость опытов Интерактивные Крестики-нолики. Решение квадратных уравнений
Интерактивные Крестики-нолики. Решение квадратных уравнений