Содержание
- 2. Вычисление производной путем логарифмирования. Функцию вида называют показательно-степенной или сложной показательной функцией.
- 5. 1. Продифференцировать функцию:
- 6. 2. Продифференцировать функцию:
- 8. Ответ:
- 9. 3. Продифференцировать функцию:
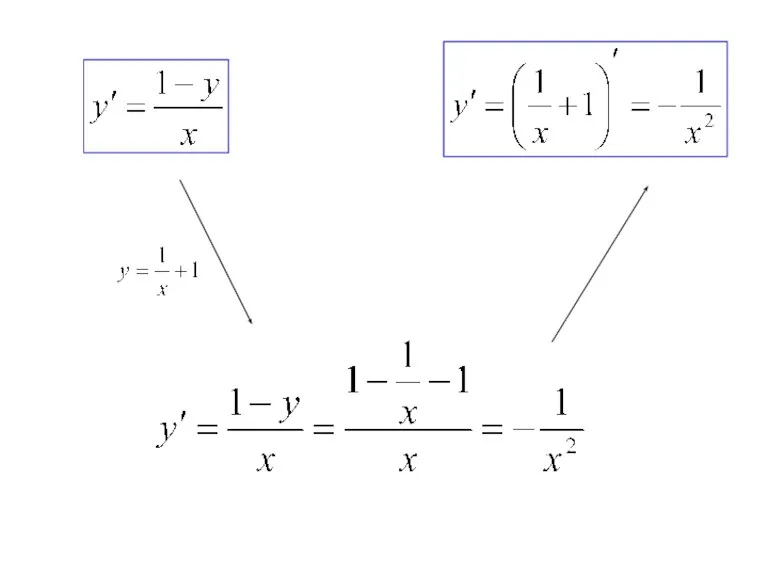
- 13. Производная неявной функции. явная функция неявная функция y=f(x) y-f(x)=0 или F(x,y)=0
- 14. Пусть
- 16. 4. Продифференцировать функцию: Ответ:
- 17. Производная функции, заданная параметрически. Пусть - обратная для функции Тогда функцию y=f(x) можно рассматривать как сложную
- 18. По правилу дифференцирования сложной функции, получим: теорема о дифференцировании обратной функции
- 20. Скачать презентацию

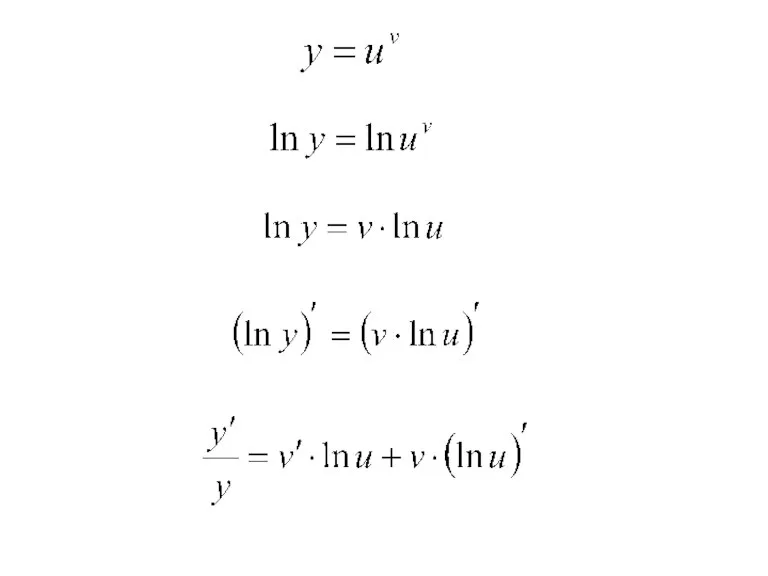



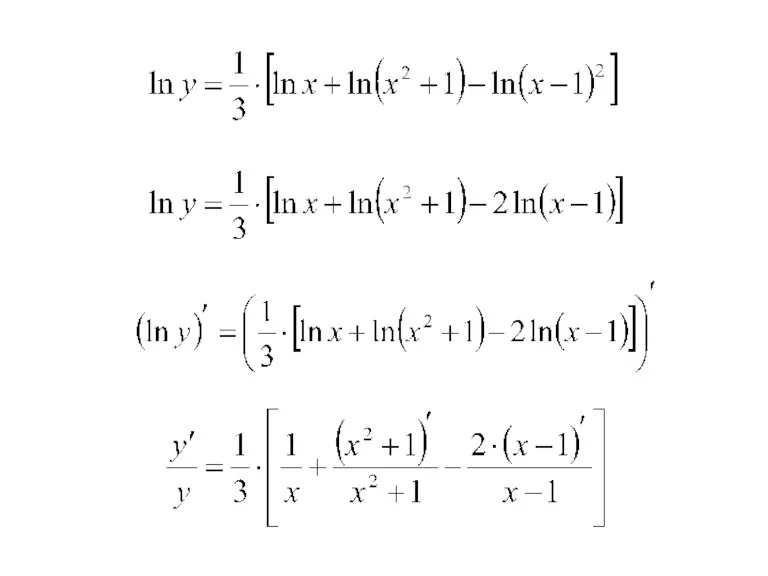
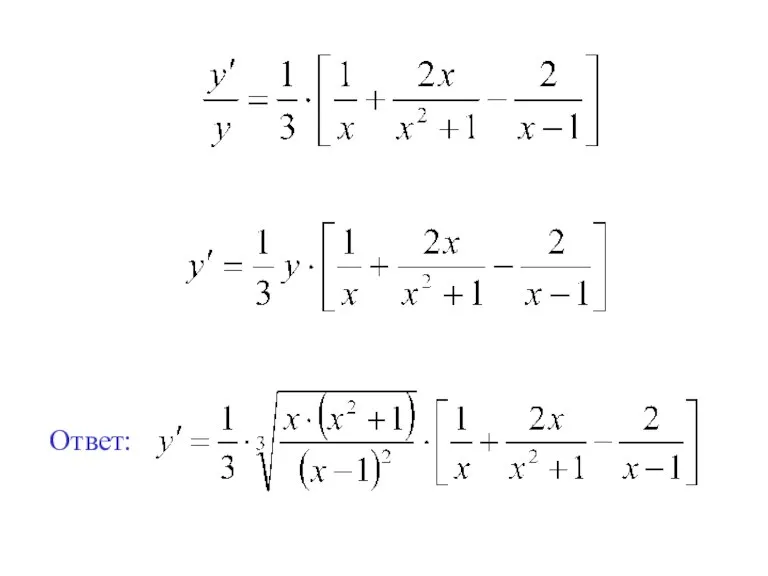


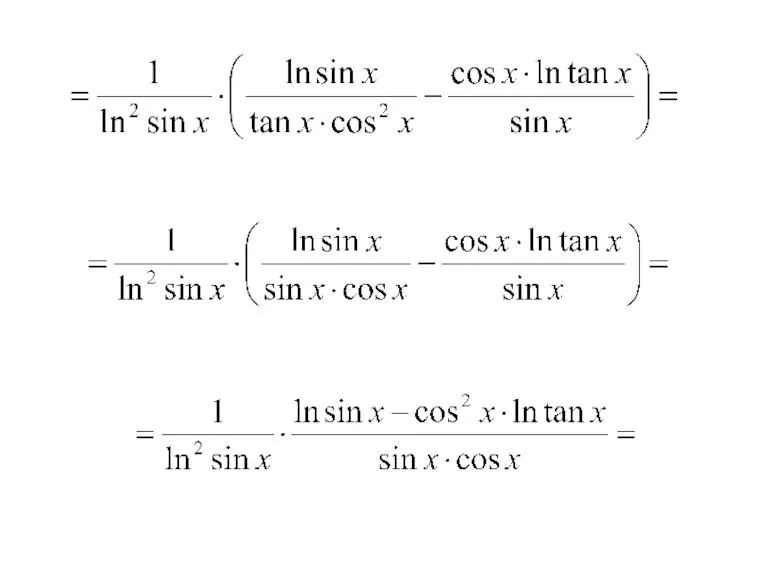
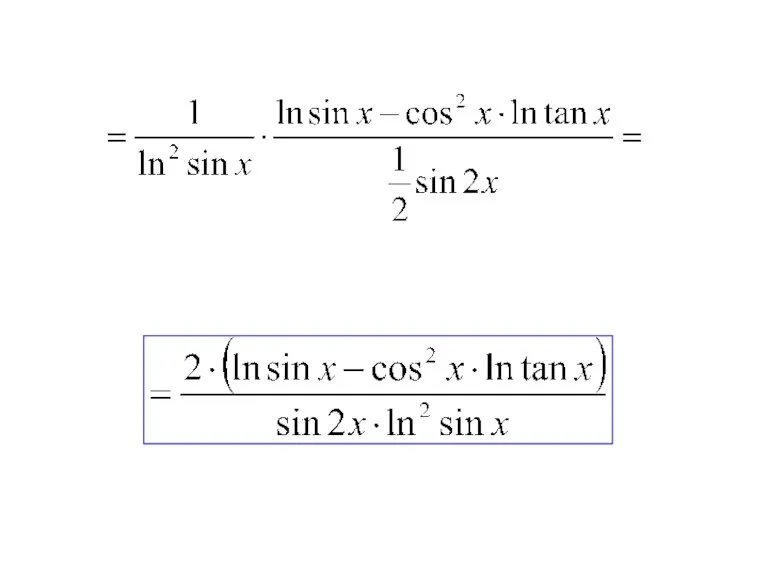





 mypresentation.ru
mypresentation.ru Четырехугольники
Четырехугольники Тестовые задания в формате ГИА. К уроку алгебры в 8 классе
Тестовые задания в формате ГИА. К уроку алгебры в 8 классе Изучение таблицы деления
Изучение таблицы деления Математическая викторина
Математическая викторина Знаки коэффициентов квадратичной функции
Знаки коэффициентов квадратичной функции Площадь многоугольника
Площадь многоугольника Статистика. Статистика знает всё (Ильф и Петров). Выборочные исследования
Статистика. Статистика знает всё (Ильф и Петров). Выборочные исследования Задачи на проценты
Задачи на проценты Решение уравнений (урок 3). 6 класс
Решение уравнений (урок 3). 6 класс Умножение натуральных чисел 5 класс
Умножение натуральных чисел 5 класс Основные правила дифференцирования
Основные правила дифференцирования delenie_s_ostatkom-_2_
delenie_s_ostatkom-_2_ Решение задач с помощью чертежа
Решение задач с помощью чертежа Умножение многочлена на многочлен
Умножение многочлена на многочлен Натуральные и целые числа. Проверочная работа
Натуральные и целые числа. Проверочная работа Precvičujeme. Správne riešenia
Precvičujeme. Správne riešenia Алгоритмы направленного перебора
Алгоритмы направленного перебора Оптимальное управление динамических систем. Гамильтониан и принцип максимума
Оптимальное управление динамических систем. Гамильтониан и принцип максимума Понятие вектора. Равенство векторов
Понятие вектора. Равенство векторов Задача 3. Построить матрицу поворота
Задача 3. Построить матрицу поворота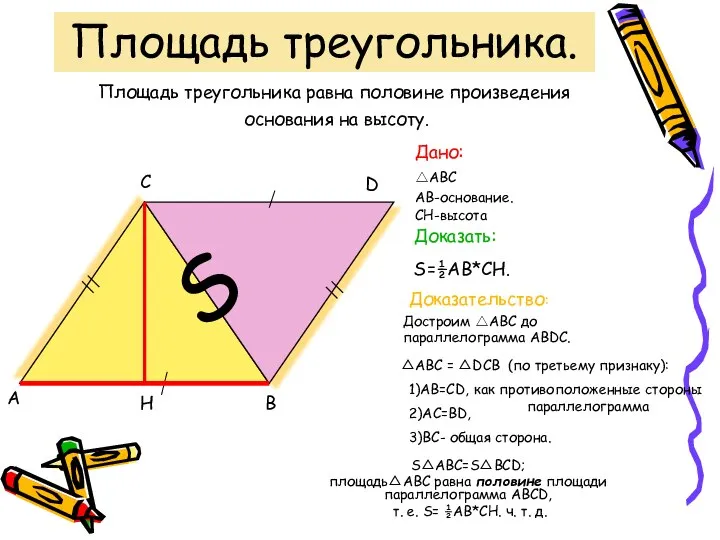 Площадь треугольника
Площадь треугольника Применение производной к исследованию функций
Применение производной к исследованию функций Вычитание дробных чисел. 5 класс
Вычитание дробных чисел. 5 класс Шар. Куб. Параллелепипед
Шар. Куб. Параллелепипед Координатная плоскость
Координатная плоскость Арксинус. Решение уравнения sin t = a. 10 класс
Арксинус. Решение уравнения sin t = a. 10 класс Сумма углов треугольника
Сумма углов треугольника