Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике)

Физический смысл
производной

Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
Задача №1
Ответ: 60 м/с.

Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 6 с.
Задача №2
Ответ: 20 м/с.

Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 6 с.
Задача №3
Ответ: 59 м/с.

Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Задача №4
Ответ: 7с.

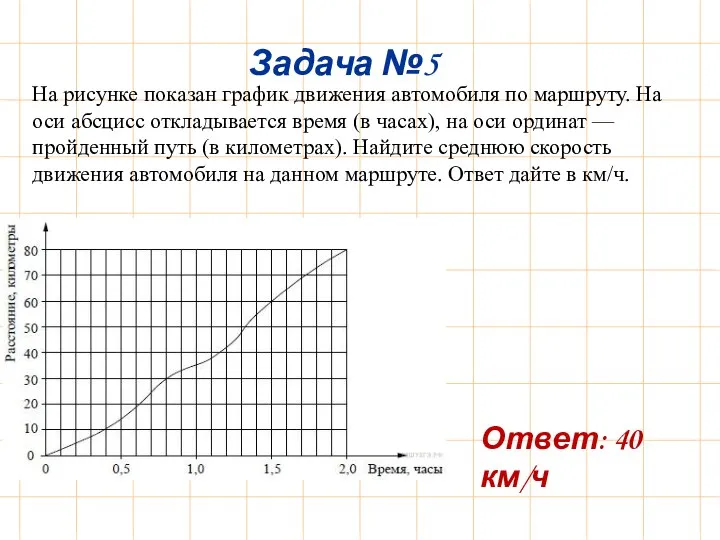
Задача №5
На рисунке показан график движения автомобиля по маршруту. На оси абсцисс откладывается время (в часах), на оси ординат — пройденный путь (в километрах). Найдите среднюю скорость движения автомобиля на данном маршруте. Ответ дайте в км/ч.
Ответ: 40 км/ч

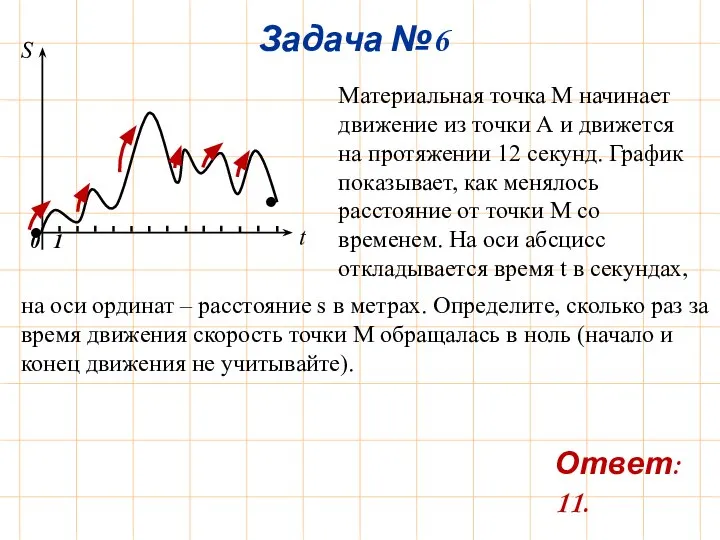
Задача №6
Материальная точка М начинает движение из точки А и движется на протяжении 12 секунд. График показывает, как менялось расстояние от точки М со временем. На оси абсцисс откладывается время t в секундах,
на оси ординат – расстояние s в метрах. Определите, сколько раз за время движения скорость точки М обращалась в ноль (начало и конец движения не учитывайте).
Ответ: 11.

Геометрический смысл производной, касательная

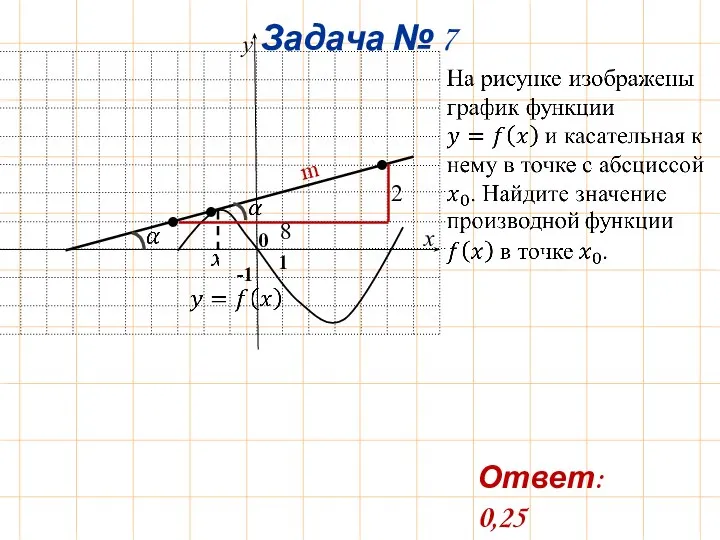
2
8
m
0
Ответ: 0,25

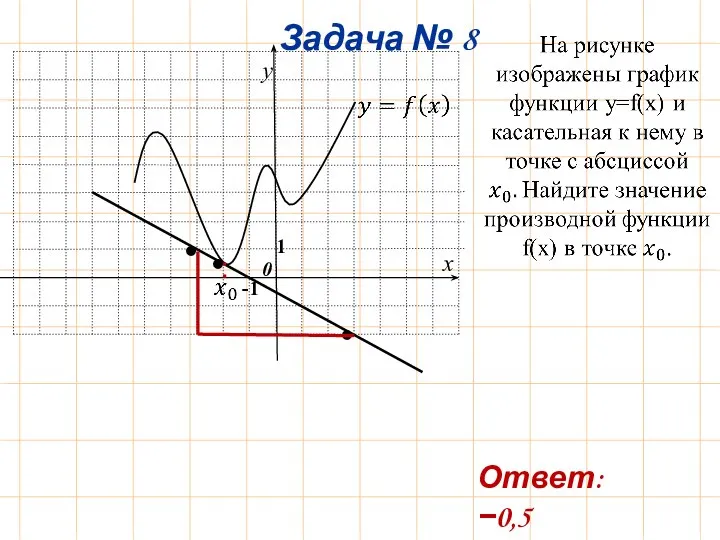
0
Ответ: −0,5

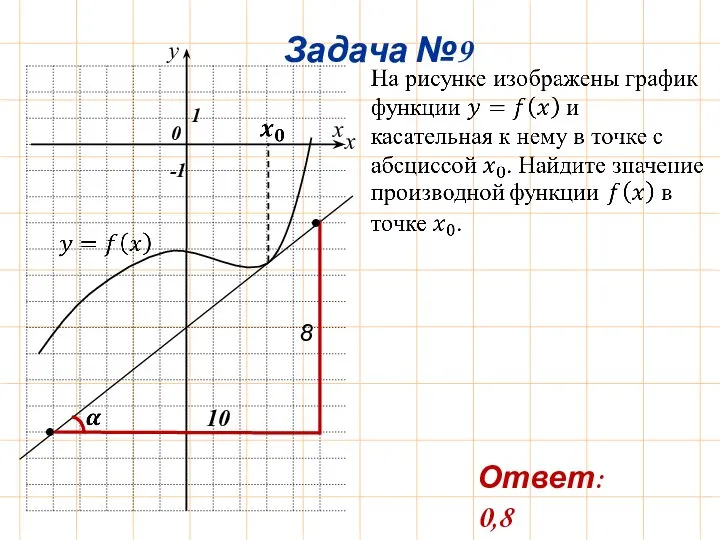
Задача №9
y
x
0
1
-1
8
10
x
•
•
Ответ: 0,8

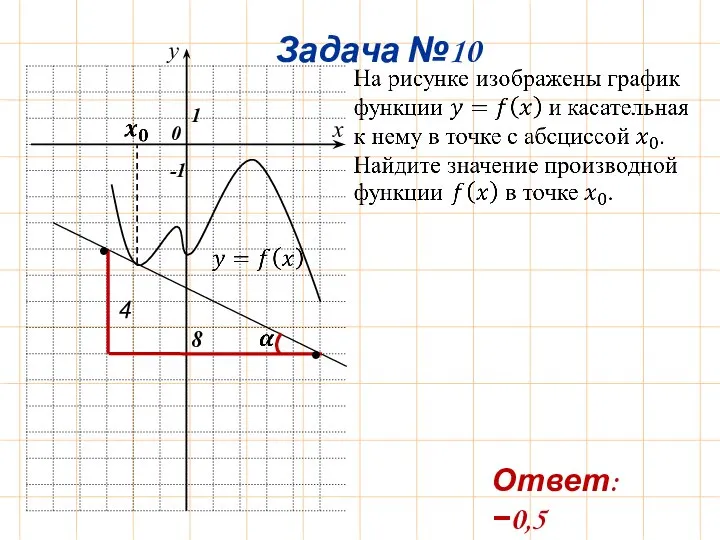
Задача №10
0
x
1
-1
y
4
8
•
•
Ответ: −0,5

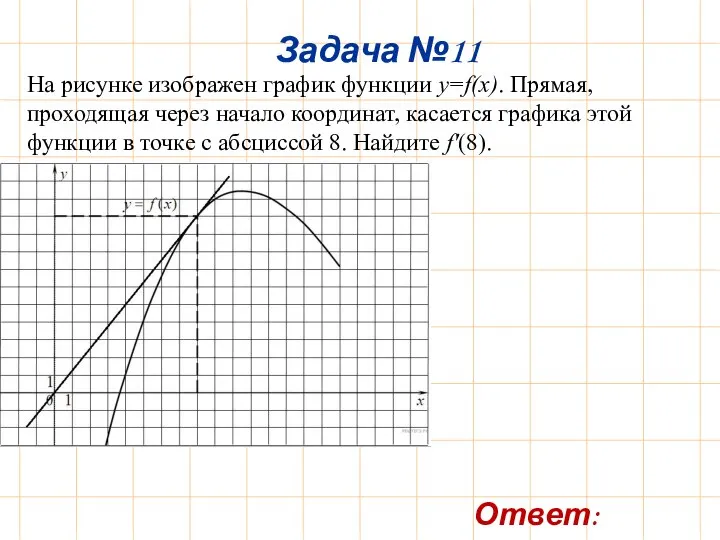
На рисунке изображен график функции y=f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите f'(8).
Задача №11
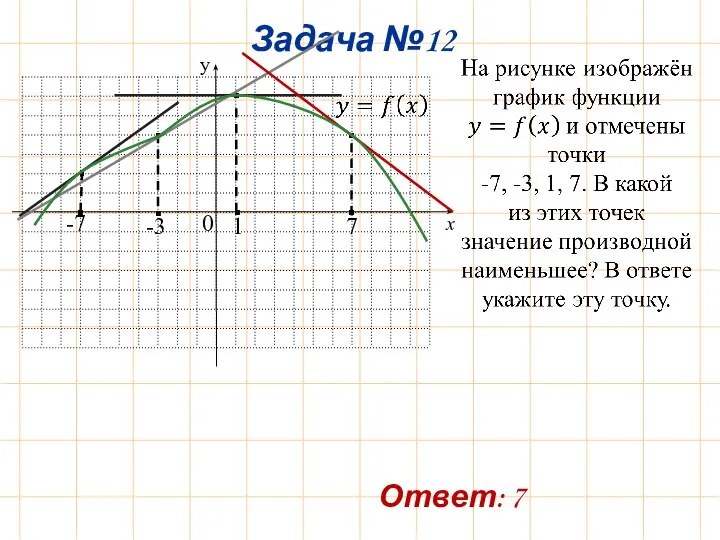
Ответ: 1,25

Задача №12
y
x
-7
-3
0
1
7
Ответ: 7

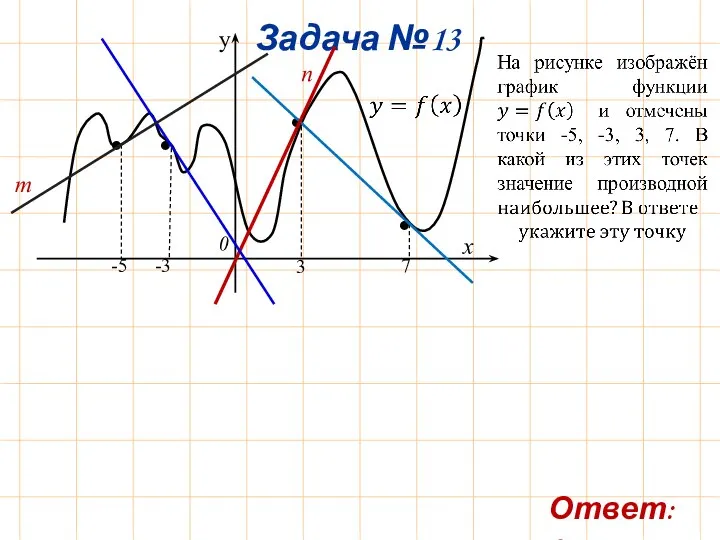
Задача №13
m
n
Ответ: 3

Применение производной
к исследованию
функций

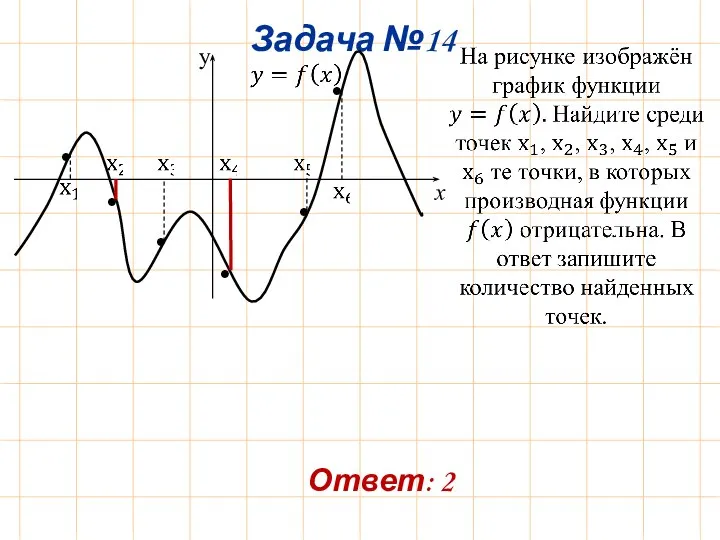
Задача №14
Ответ: 2

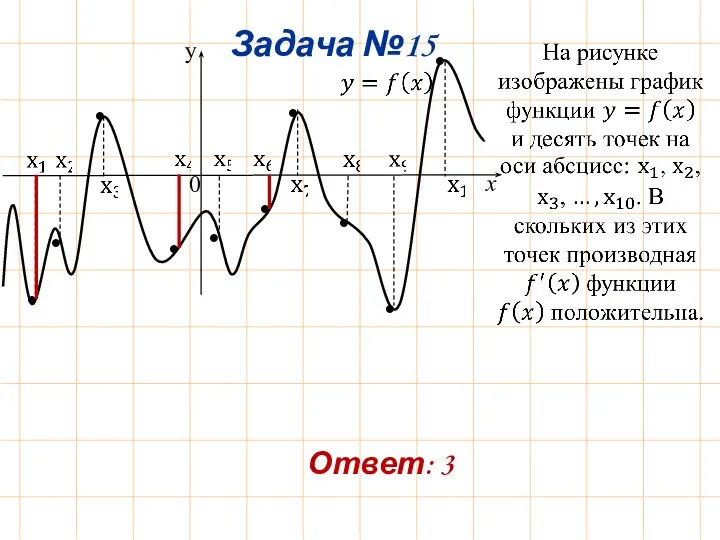
Задача №15
Ответ: 3

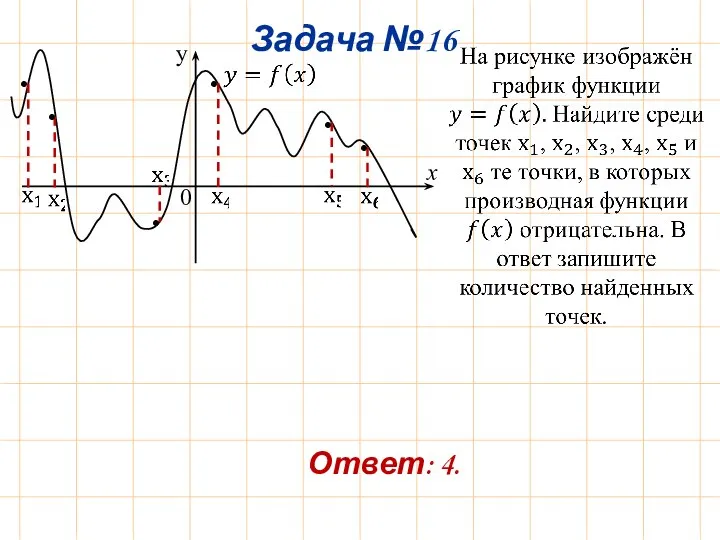
Задача №16
Ответ: 4.

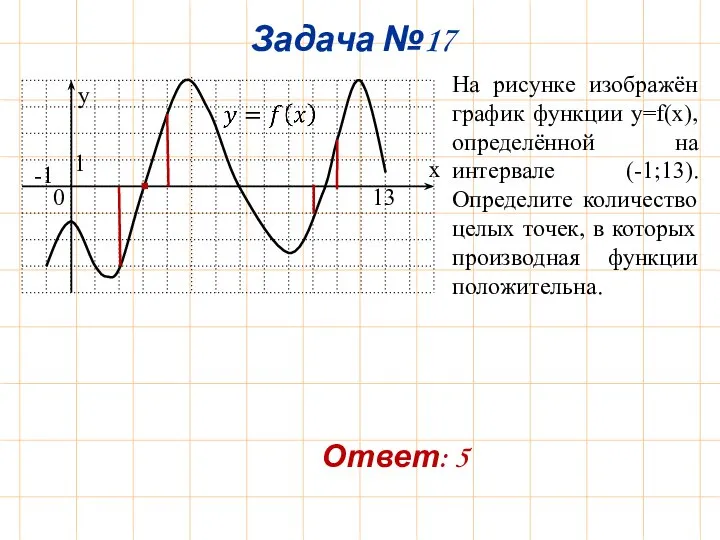
Задача №17
y
x
0
1
-1
13
На рисунке изображён график функции y=f(x), определённой на интервале (-1;13). Определите количество целых точек, в которых производная функции положительна.
Ответ: 5

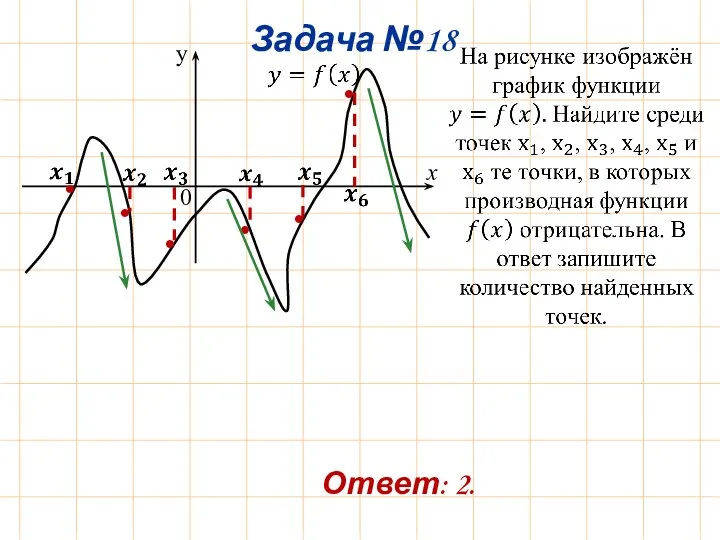
Задача №18
y
Ответ: 2.

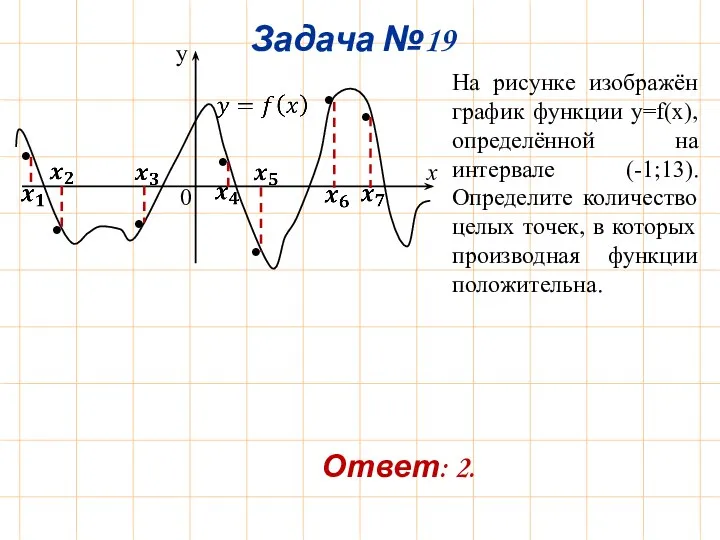
y
x
Задача №19
0
•
•
•
•
•
•
•
На рисунке изображён график функции y=f(x), определённой на интервале (-1;13). Определите количество целых точек, в которых производная функции положительна.
Ответ: 2.

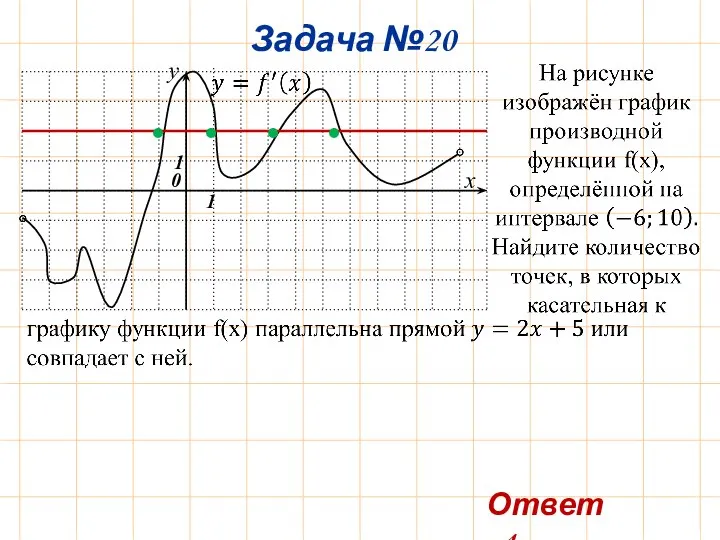
Задача №20
y
x
0
1
1
•
•
•
•
Ответ: 4.

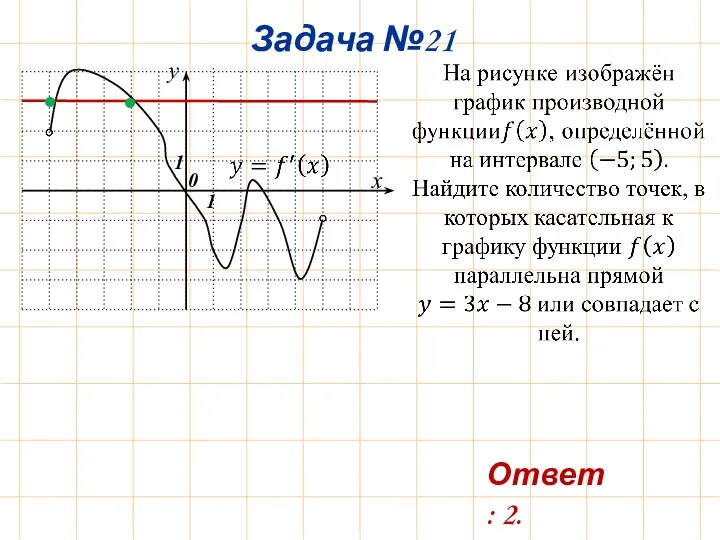
Задача №21
y
x
0
1
1
•
•
Ответ: 2.

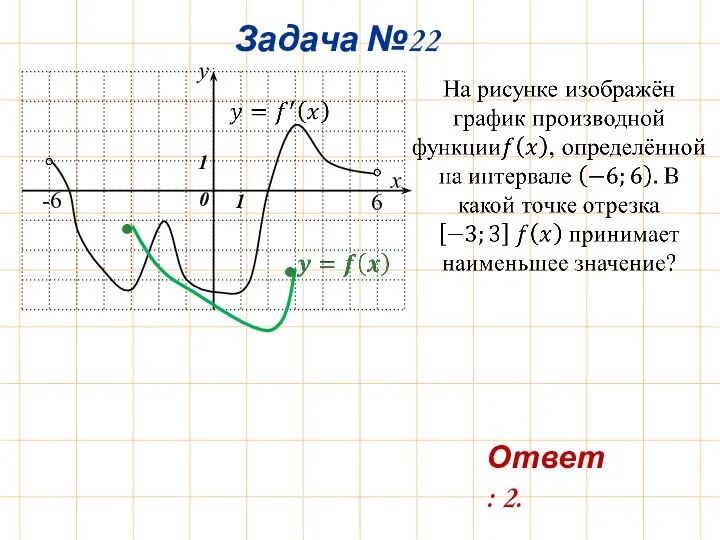
Задача №22
y
x
0
1
1
-6
6
Ответ: 2.
•
•

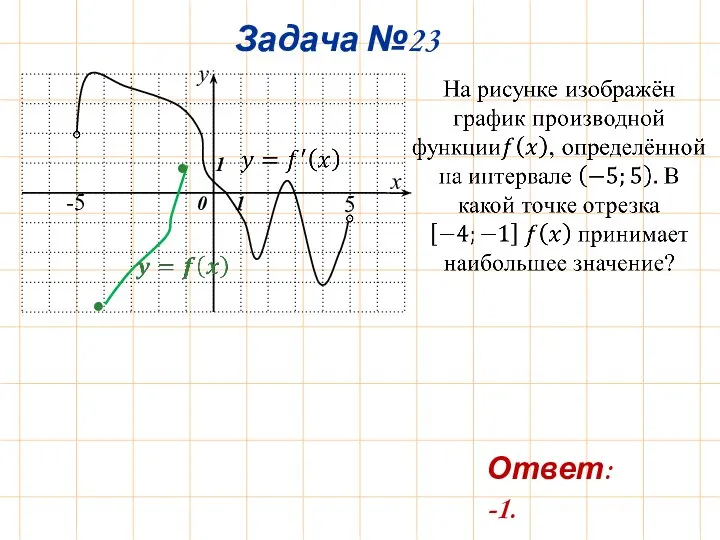
Задача №23
Ответ: -1.
•
•

Задача №24
Задача №25
Ответ: 1.
Ответ: -0,5.
Прямая y = 6x + 9 параллельна касательной к графику функции
y = x2 + 7x − 6. Найдите абсциссу точки касания.
Прямая y = − 4x − 8 является касательной к графику функции
y = x3 − 3x2 − x − 9. Найдите абсциссу точки касания.

Задача №26
Ответ: 2.
Прямая y = 5x + 14 является касательной к графику функции
y = x3 − 4x2 + 9 x +14. Найдите абсциссу точки касания.

Прямая y = 3x + 4 является касательной к графику функции
y = x3 + 4x2 + 3x + 4. Найдите ординату точки касания.
Задача №27
Решение.
Значение производной функции в точке касания
равно угловому коэффициенту касательной, т. е. y / = 3
y / = 3 x2 + 8x + 3
3 x2 + 8x + 3 = 3
x(3x+8) = 0. Отсюда x = 0 или x = 8/3
Уравнению x3 + 4x2 + 3x + 4 = 3x + 4 удовлетворяет только
x = 0. Значит, абсцисса точки касания равна 0, а тогда ее
ордината равна 4.
Ответ: 4.

Прямая y = 3x + 1 является касательной к графику функции ax2 + 2x + 3. Найдите a.
По смыслу задачи a ≠ 0, а значит, график заданной
функции − парабола. Касательная к параболе
(а также и к гиперболе) имеет с ней единственную
общую точку. Поэтому необходимо и достаточно, чтобы уравнение ax2 + 2x + 3 = 3x + 1 имело единственно решение.
Получим ax2 + 2x + 3 − 3x − 1
ax2 − x + 2 = 0
D = 1 − 8а
Для этого дискриминант должен быть равен нулю, откуда
1 − 8а = 0
a = 1/8 = 0,125
Задача №28
Решение.
Ответ: 0,125.

Прямая y = 3x + 4 является касательной к графику функции
3x2 − 3x + с . Найдите с .
Задача №29
Решение.
График заданной функции − парабола. Касательная к параболе
имеет с ней единственную общую точку. Поэтому необходимо и достаточно, чтобы уравнение 3x2 − 3x + с = 3x + 4 имело единственно решение. Получим
3x2 − 6x + с − 4 = 0
D = 36 − 12(с − 4) = 36 − 12с+ 48 = 84 − 12с
Для этого дискриминант должен быть равен нулю, откуда
84 − 12с = 0
с = 84/12 = 7
Ответ: 7.

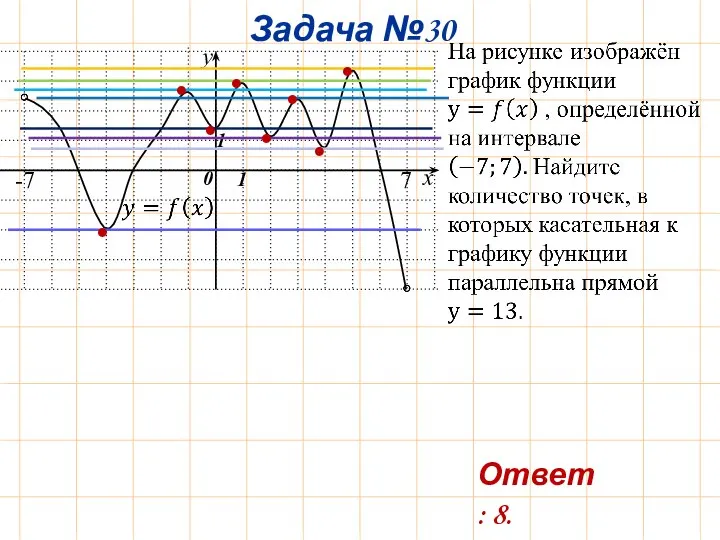
Задача №30
x
•
•
•
•
•
•
•
•
Ответ: 8.

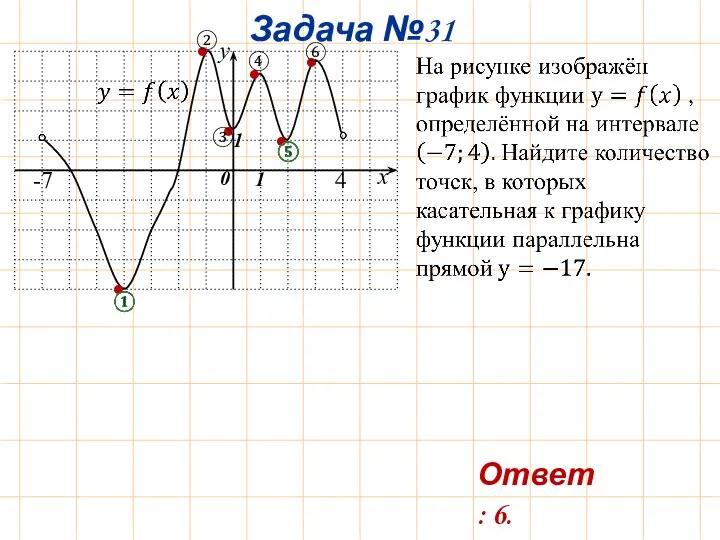
Задача №31
x
•
•
•
•
•
•
②
③
④
⑥
Ответ: 6.

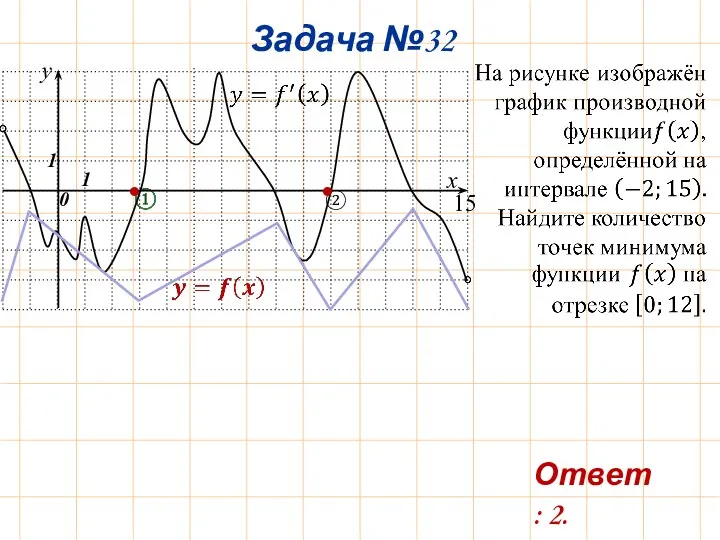
②
Задача №32
15
Ответ: 2.
•
•

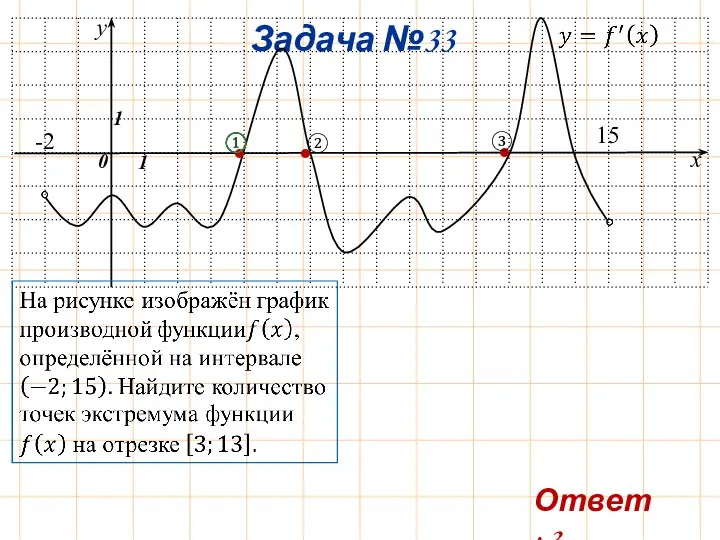
Задача №33
y
x
0
1
1
-2
15
Ответ: 3.
•
•
•
②
③

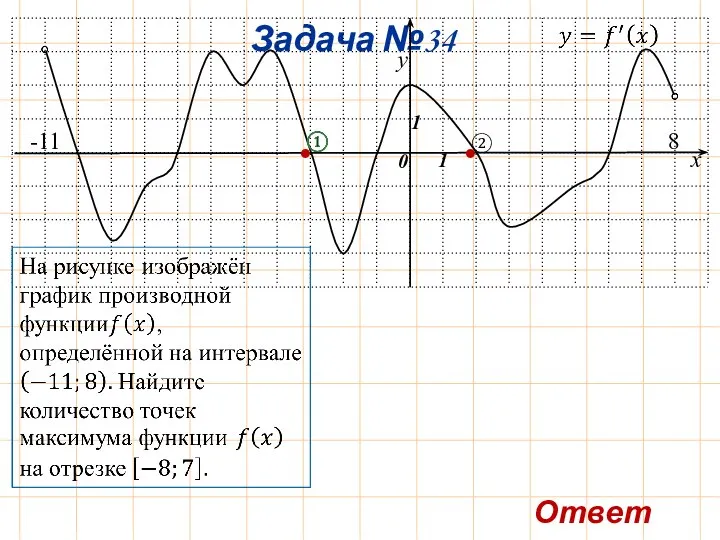
Задача №34
y
x
0
1
1
-11
8
Ответ: 2.
②
•
•

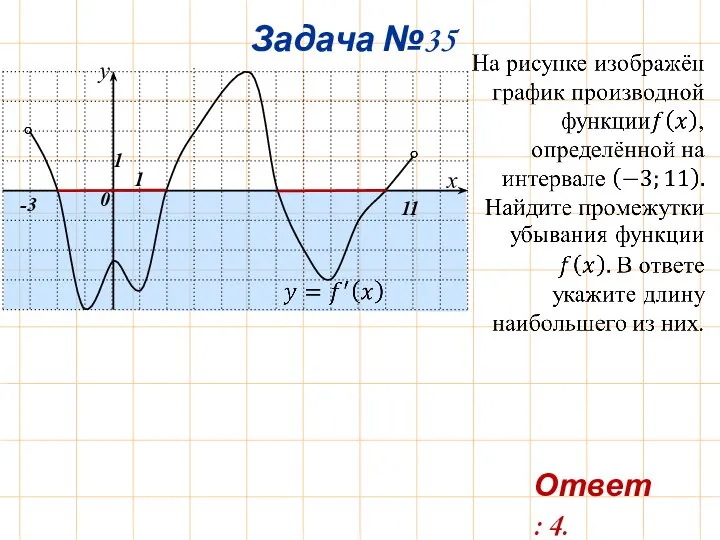
Задача №35
-3
11
Ответ: 4.

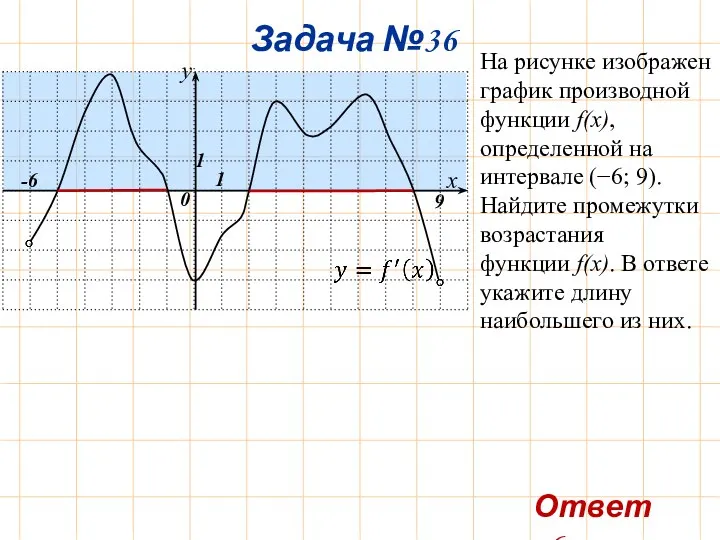
Задача №36
-6
9
Ответ: 6.
На рисунке изображен график производной функции f(x), определенной на интервале (−6; 9). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

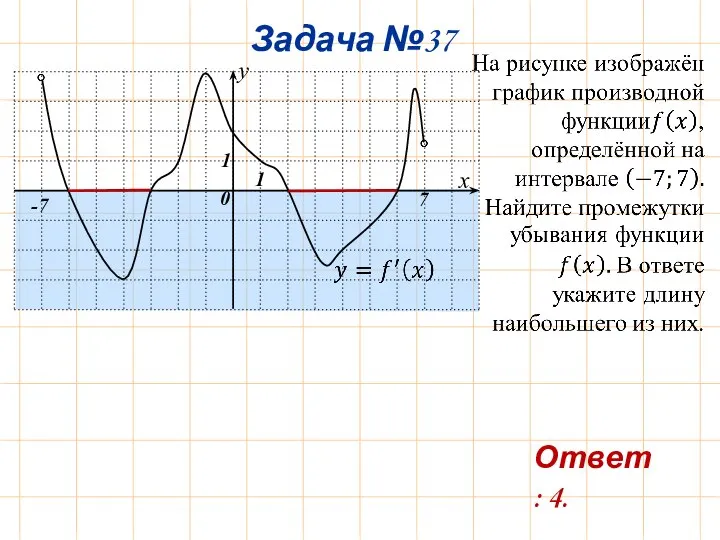
Задача №37
7
-7
Ответ: 4.

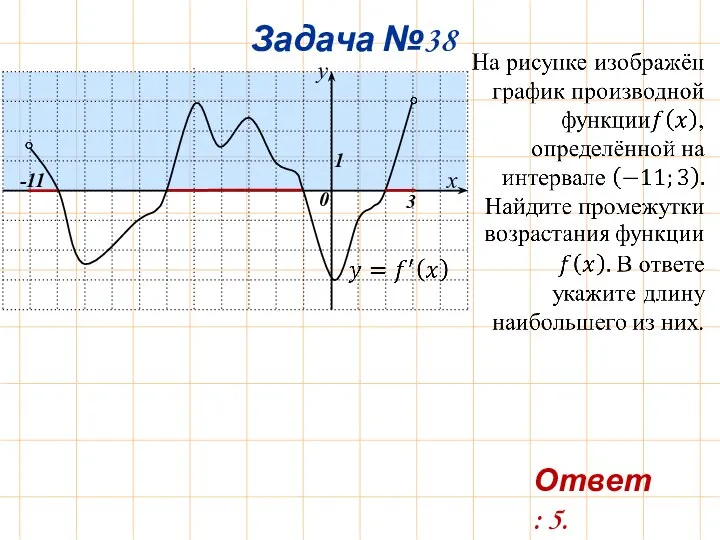
Задача №38
-11
3
Ответ: 5.

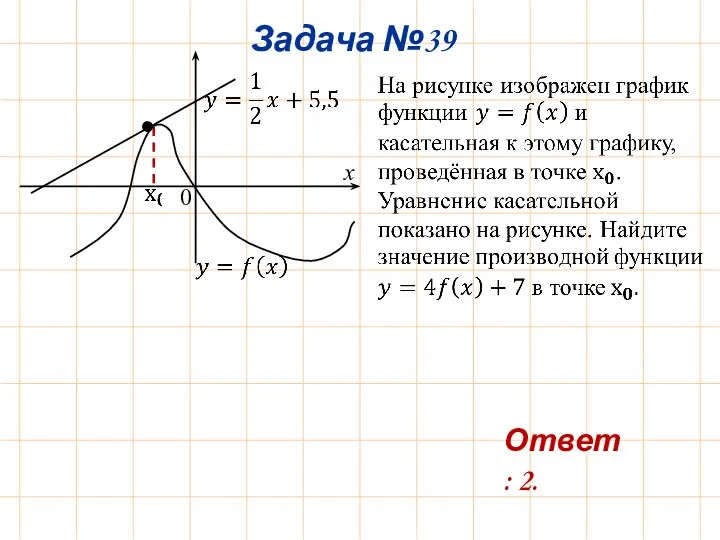
Задача №39
0
x
•
Ответ: 2.

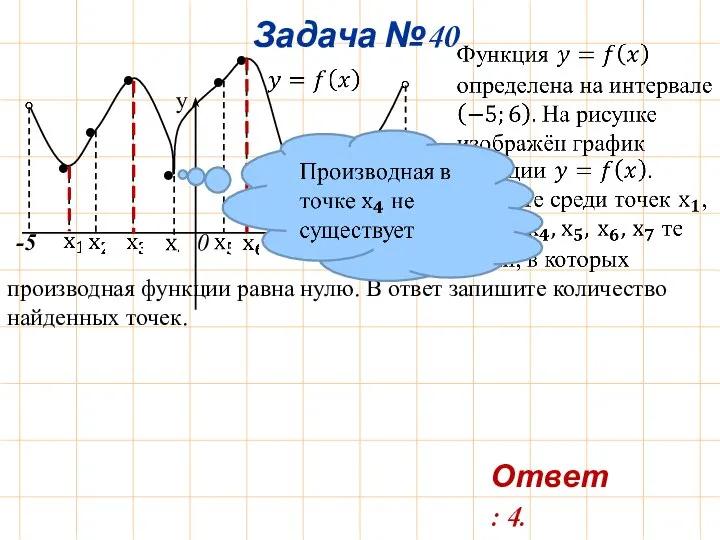
y
0
x
•
•
•
•
•
Задача №40
•
•
-5
6
производная функции равна нулю. В ответ запишите количество найденных точек.
Ответ: 4.

Первообразная
Интеграл