Содержание
- 2. В задаче C2 рассматриваются многогранники, на основе которых, как правило, нужно найти одну из следующих величин:
- 3. Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три: Главная формула — косинус
- 4. Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12;
- 5. Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1;
- 6. Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений: Получили, что
- 7. Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора,
- 8. Вычисление координат векторов Теорема. Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.
- 9. Введение системы координат Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения,
- 16. Решение задач методом координат упрощает знание опорной задачи:
- 17. Угол между прямыми
- 18. Решение (1 способ)
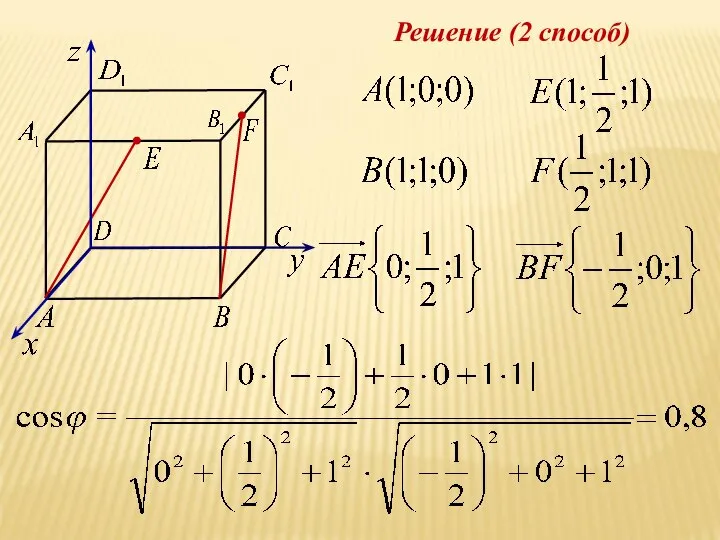
- 19. Решение (2 способ)
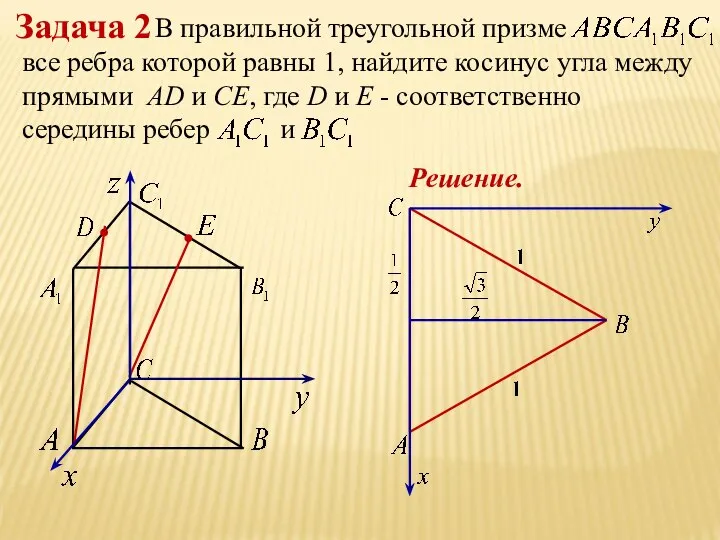
- 20. Решение.
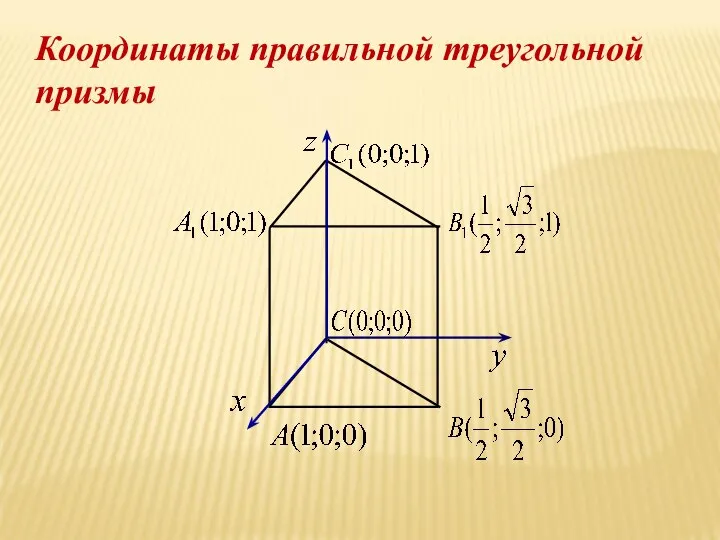
- 21. Координаты правильной треугольной призмы
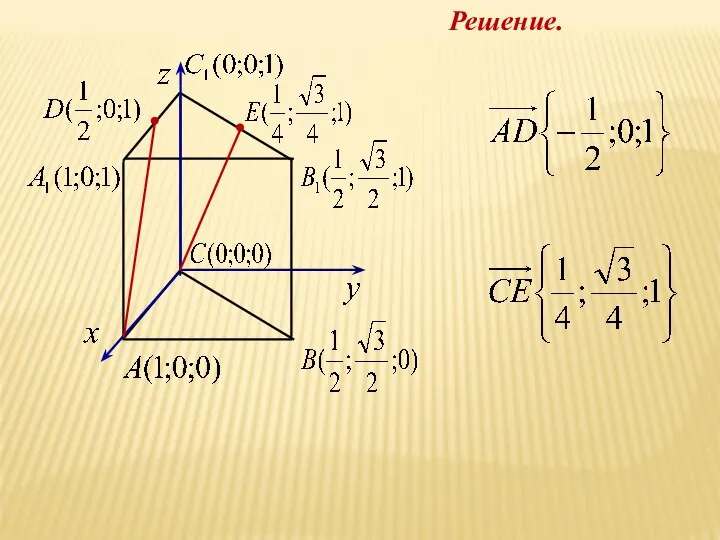
- 22. Решение.
- 24. Решение.
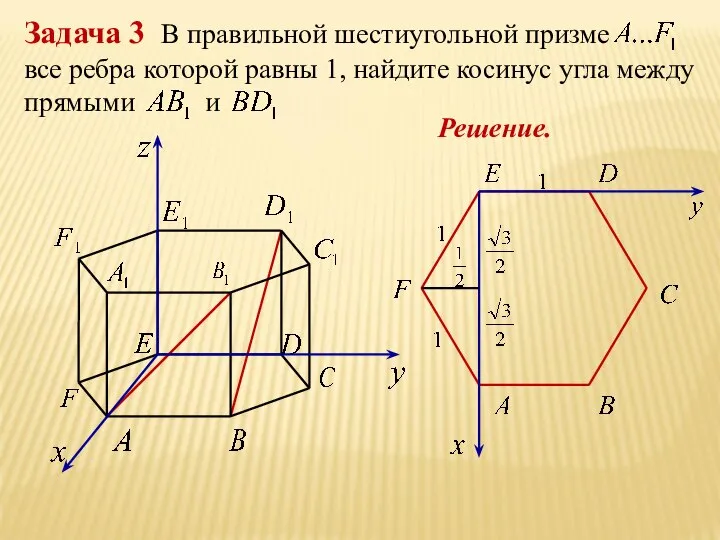
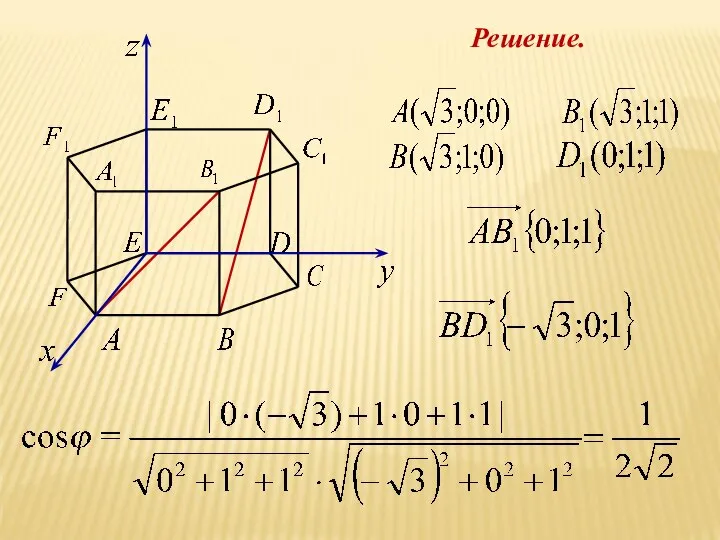
- 25. Координаты правильной шестиугольной призмы
- 26. Решение.
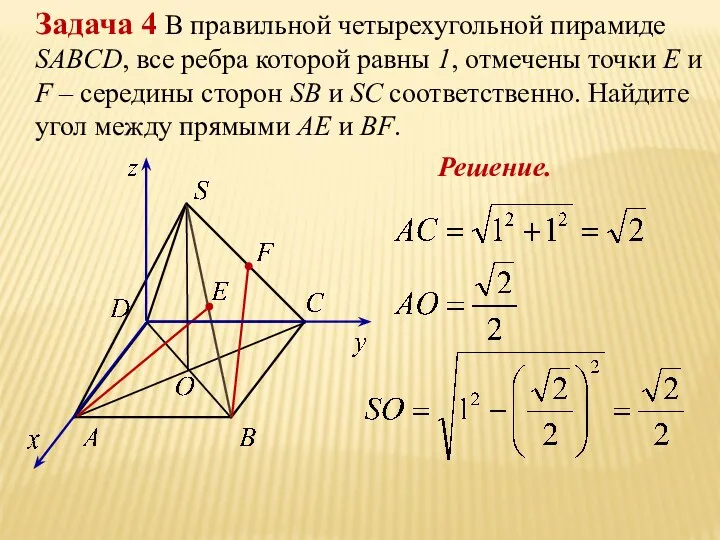
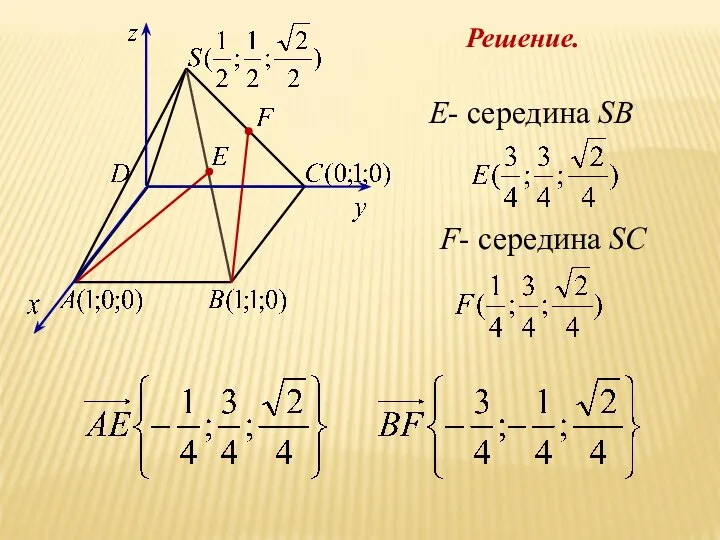
- 27. Задача 4 В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, отмечены точки Е и
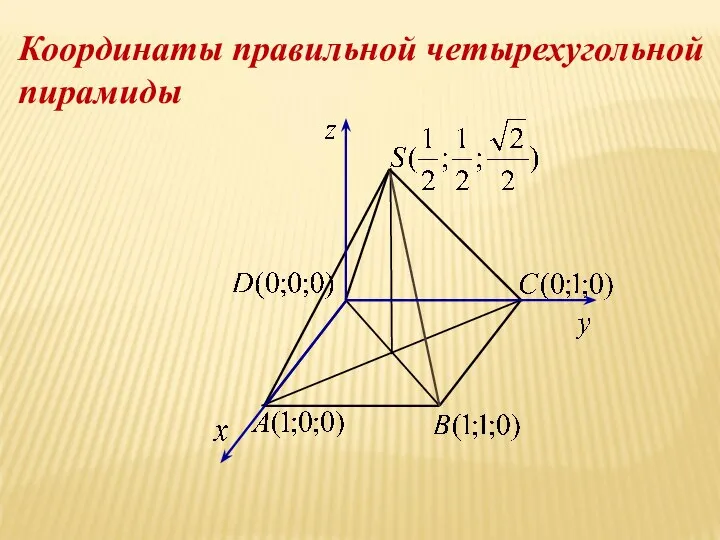
- 28. Координаты правильной четырехугольной пирамиды
- 29. Е- середина SB F- середина SC Решение.
- 31. Скачать презентацию

















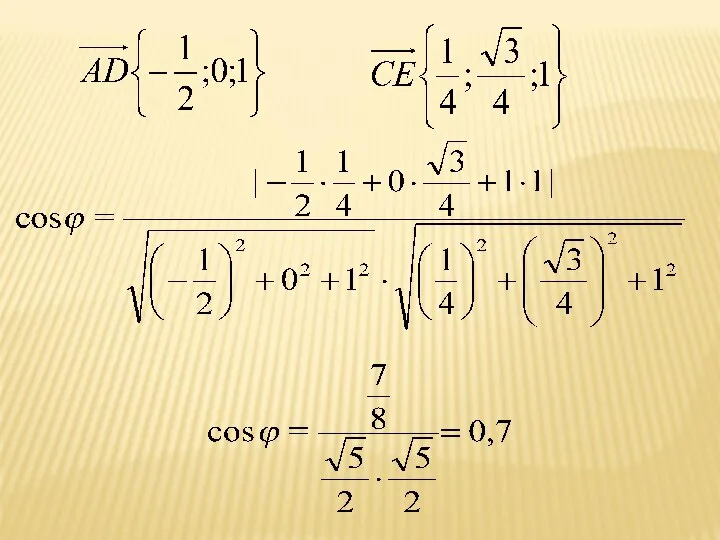

 История развития обыкновенных дробей
История развития обыкновенных дробей Свойства логарифмов
Свойства логарифмов Приёмы вычитания с переходом через десяток
Приёмы вычитания с переходом через десяток Счет в пределах 5
Счет в пределах 5 Сложение двузначных и однозначных чисел с переходом в другой разряд
Сложение двузначных и однозначных чисел с переходом в другой разряд Сравнение, сложение и вычитание обыкновенных дробей. 6 класс
Сравнение, сложение и вычитание обыкновенных дробей. 6 класс Геро́н Александри́йский
Геро́н Александри́йский Умножение числа на произведение
Умножение числа на произведение Определение расстояния по градусной сети
Определение расстояния по градусной сети Введение в аналитическую геометрию. Векторы на плоскости и в пространстве
Введение в аналитическую геометрию. Векторы на плоскости и в пространстве Презентация на тему Линейная функция (7 класс)
Презентация на тему Линейная функция (7 класс)  Теорема Безу (теорема об остатке и разложение на множители)
Теорема Безу (теорема об остатке и разложение на множители) Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма
Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма Теорема косинусов
Теорема косинусов Равнобедренный треугольник. Окружность
Равнобедренный треугольник. Окружность Круговая окружность
Круговая окружность Презентация на тему Угол поворота. Радианная мера угла
Презентация на тему Угол поворота. Радианная мера угла  Приёмы устных вычислений в пределах 1000
Приёмы устных вычислений в пределах 1000 Планирование эксперимента. Логические основы
Планирование эксперимента. Логические основы Психогеометрия
Психогеометрия Презентация на тему Закон больших чисел. Теорема Чебышева
Презентация на тему Закон больших чисел. Теорема Чебышева  Умножение и деление десятичной дроби на 10, 100, 1000
Умножение и деление десятичной дроби на 10, 100, 1000 Таблицы истинности
Таблицы истинности Сложение векторов
Сложение векторов Построение таблиц истинности
Построение таблиц истинности Стандартный вид числа в физике, астрономии и технике
Стандартный вид числа в физике, астрономии и технике Площадь трапеции
Площадь трапеции Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора Иоганн Кеплер
Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора Иоганн Кеплер