Угол между прямой и плоскостью (Задание 13)

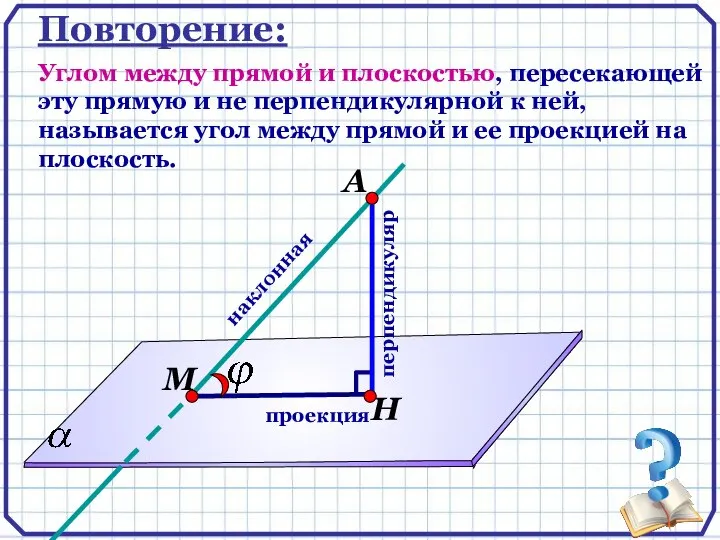
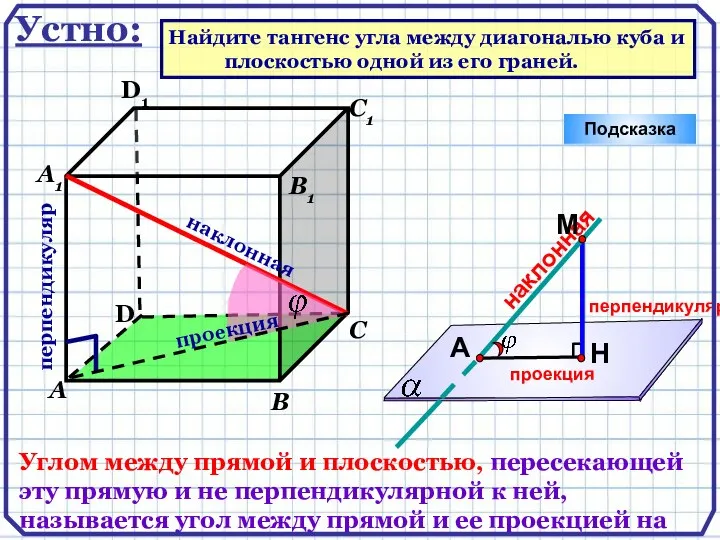
Повторение:
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
перпендикуляр
наклонная

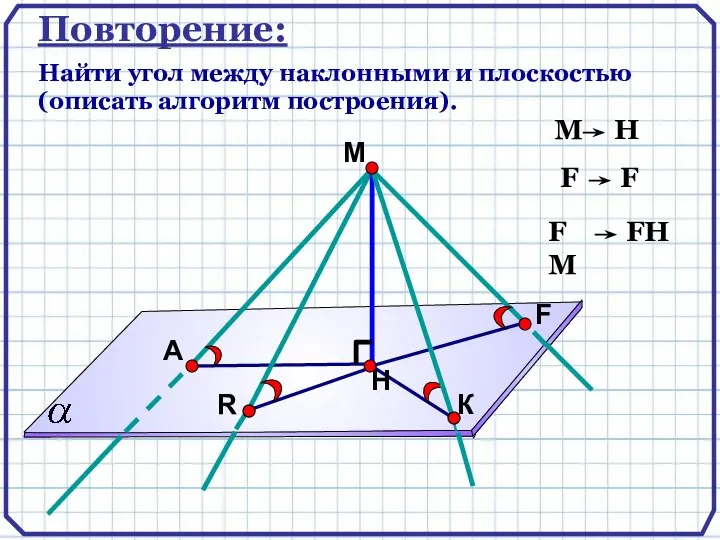
Повторение:
Найти угол между наклонными и плоскостью
(описать алгоритм построения).

Повторение:
1) Если этот угол удается включить в прямоугольный треугольник в качестве одного из острых углов;
Угол между прямой m и плоскостью α можно вычислить:
4) Используя ключевые задачи;
3) Используя координатно –векторный метод;
2) Используя векторный метод;

D
А
В
С
А1
D1
С1
В1
Подсказка
перпендикуляр
наклонная
Устно:
Найдите тангенс угла между диагональю куба и
плоскостью одной из его граней.

В единичном кубе АВСДА1В1С1Д1 найдите
тангенс угла между прямой АА1 и
плоскостью ВС1Д .
№ 1
1
1
1
1
1) Прямая AА1 параллельна прямой СС1, ⇒Угол между прямой АА1 и плоскостью ВС1Д .
равен углу между СС1 и плоскостью ВС1Д.
2. Прямая СС1 проецируется на плоскость ВС1Д в прямую ОС1. Поэтому проекция точки С лежит на отрезке ОС1. Значит, прямая ОС1 является проекцией прямой СС1, следовательно, угол ОС1С искомый.
О

Критерии оценивания выполнения задания С2

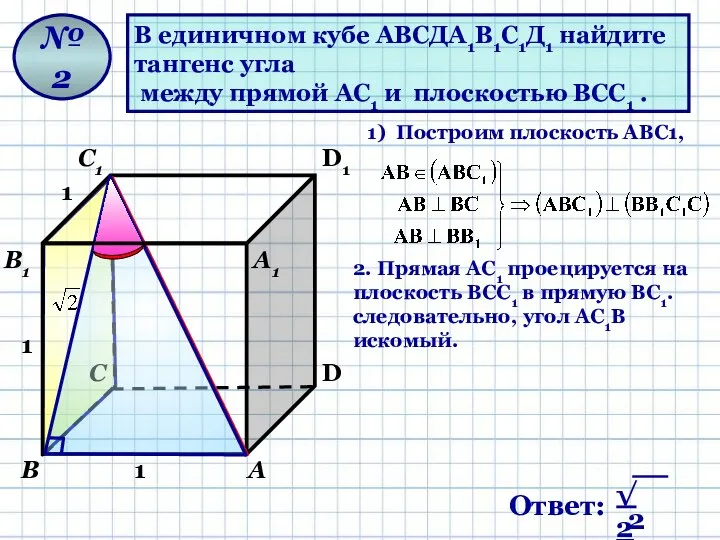
В единичном кубе АВСДА1В1С1Д1 найдите
тангенс угла
между прямой АС1 и плоскостью ВСС1 .
№ 2
1) Построим плоскость AВС1,
2. Прямая АС1 проецируется на плоскость ВСС1 в прямую ВС1. следовательно, угол АС1В искомый.
1
1
1

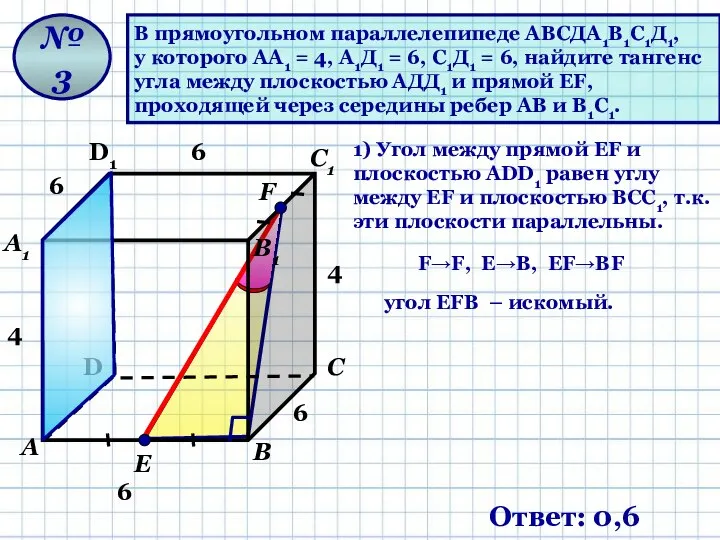
В прямоугольном параллелепипеде АВСДА1В1С1Д1,
у которого АА1 = 4, А1Д1 = 6, С1Д1 = 6, найдите тангенс
угла между плоскостью АДД1 и прямой ЕF,
проходящей через середины ребер АВ и В1С1.
№ 3
Ответ: 0,6
1) Угол между прямой EF и плоскостью АDD1 равен углу между EF и плоскостью ВСС1, т.к. эти плоскости параллельны.
F→F, Е→В, ЕF→ВF
угол EFB – искомый.
4
4
6
6
6
6

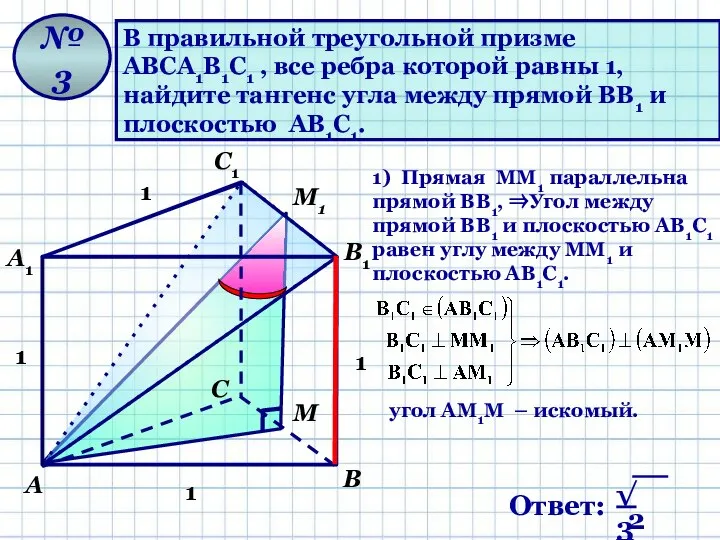
В правильной треугольной призме
АВСА1В1С1 , все ребра которой равны 1,
найдите тангенс угла между прямой ВВ1 и
плоскостью АВ1С1.
№ 3
1
1
1
1
М
М1
1) Прямая ММ1 параллельна прямой ВВ1, ⇒Угол между прямой ВВ1 и плоскостью АВ1С1
равен углу между ММ1 и плоскостью АВ1С1.
угол АМ1М – искомый.

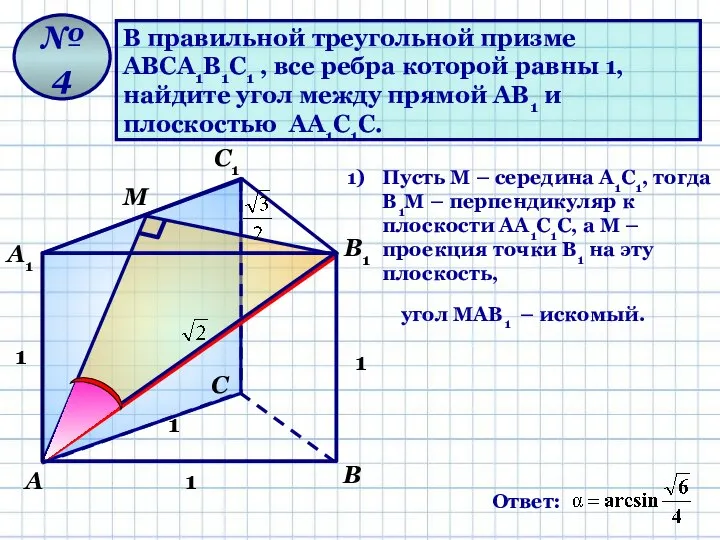
В правильной треугольной призме
АВСА1В1С1 , все ребра которой равны 1,
найдите угол между прямой АВ1 и
плоскостью АА1С1С.
№ 4
1
1
1
1
М
Ответ:
угол МАВ1 – искомый.
Пусть М – середина А1С1, тогда В1М – перпендикуляр к плоскости АА1С1С, а М – проекция точки В1 на эту плоскость,

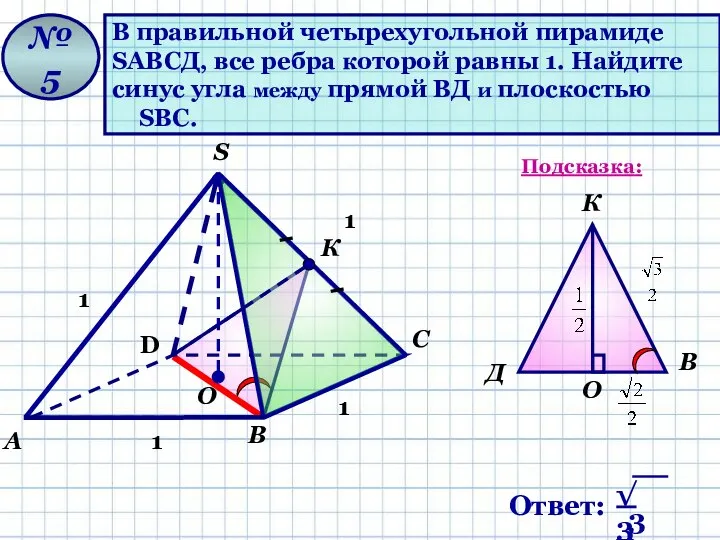
В правильной четырехугольной пирамиде
SАВСД, все ребра которой равны 1. Найдите
синус угла между прямой ВД и плоскостью SВС.
№ 5
1
1
1
1
Подсказка:

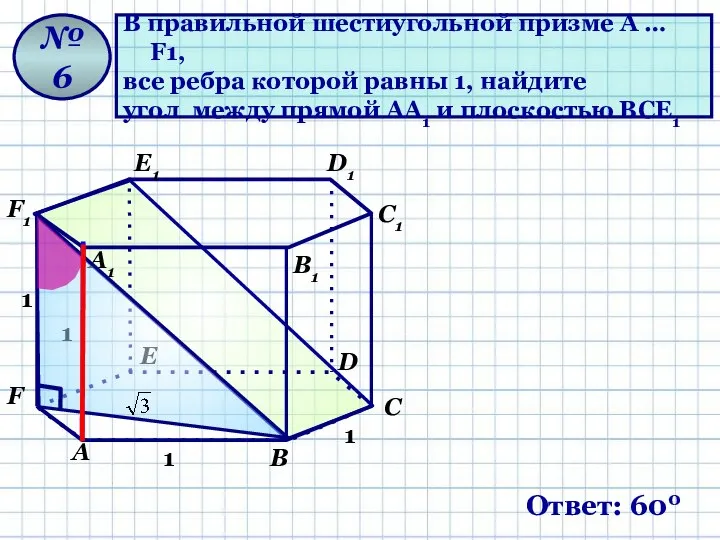
В правильной шестиугольной призме A … F1,
все ребра которой равны 1, найдите
угол между прямой AА1 и плоскостью BCЕ1
№ 6
1
1
1
Ответ: 600
1

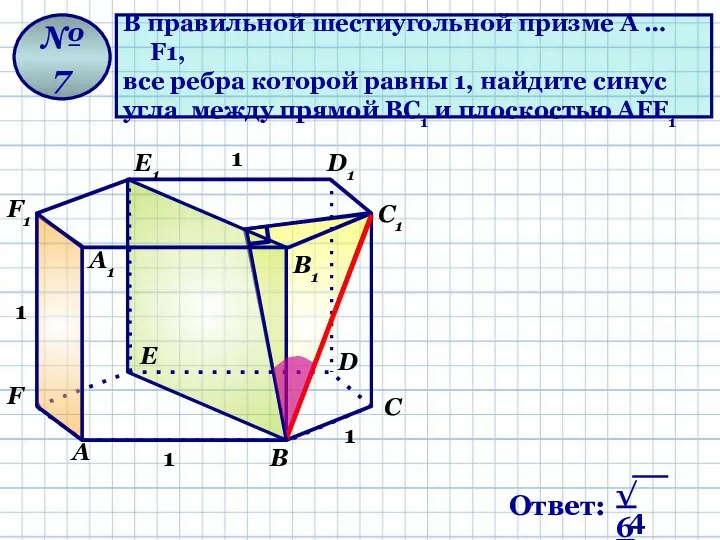
В правильной шестиугольной призме A … F1,
все ребра которой равны 1, найдите синус
угла между прямой BС1 и плоскостью АFF1
№ 7
1
1
1
1

В единичном кубе АВСДА1В1С1Д1 точка Е – середина
ребра А1В1. Найдите синус угла между прямой АЕ и
плоскостью ВДД1.
Домашнее задание
В правильной шестиугольной призме
АВСДЕFА1В1С1Д1Е1F1, все ребра которой равны 1,
найдите угол между прямой СС1 и плоскостью BДЕ1 .
В прямоугольном параллелепипеде АВСДА1В1С1Д1,
у которого АВ = 4, ВС = 6, СС1 = 4, найдите тангенс
угла между плоскостью АВС и прямой ЕF,
проходящей через середины ребер АА1 и С1Д1.