- Главная
- Математика
- Проценты. Исследовательская работа

Содержание
- 2. Проценты встречаются в нашей жизни ежедневно. Гипотеза работы: если знать правила решения задач на проценты и
- 3. История возникновения процентов История происхождения процентов началась еще в древности. Идея выражения частей целого постоянно в
- 4. Слово "процент" происходит от латинского "pro centum", что буквально означает "за сотню" или "со ста". Определение
- 5. Типы задач на проценты в ОГЭ По содержанию задачи можно разбить на следующие группы: Прикладные задачи
- 6. Под прикладной математикой обычно понимается тот раздел математики, в котором демонстрируется применение математики в практических ситуациях.
- 7. Финансовые задачи Объектом изучения являются любые финансово-кредитные операции, которые предполагают наличие ряда условий, с которыми согласны
- 8. Сами видите, решать задачи на проценты не так уж сложно. Если усвоить основные правила и подключить
- 10. Скачать презентацию
Слайд 2Проценты встречаются в нашей жизни ежедневно.
Гипотеза работы: если знать правила решения
Проценты встречаются в нашей жизни ежедневно.
Гипотеза работы: если знать правила решения

Актуальность и практическая значимость: необходимо повышать уровень знаний учащихся во время изучения процентов в школе, так как сейчас в вариантах вступительных экзаменов встречаются задачи на проценты, и эти задачи очень часто вызывают затруднения у школьников.
Задачи работы:
Обобщить знания по теме исследования
Проанализировать литературу
Узнать историю происхождения процентов.
Найти разнообразные задачи с процентами, выяснить их методы решения.
Обобщить результаты работы
Введение
Слайд 3 История возникновения процентов
История происхождения процентов началась еще в древности. Идея
История возникновения процентов
История происхождения процентов началась еще в древности. Идея

Употребление термина «процент» в России начинается в конце XVIII в. Долгое время под процентами понималось исключительно прибыль или убыток на каждые 100 рублей. Проценты применялись только в торговых и денежных сделках. Затем область их применения расширилась.
История создания знака процент
Существует две версии происхождения знака %. Одна из версий, больше похожая на вымысел, это ошибка наборщика, который, набирая в 1685 году в Париже книгу под названием "Руководство по коммерческой арифметике" Матье де ла Порта, по ошибке вместо слова "cto" поставил знак %.
По второй, более правдоподобной версии, знак % это упрощение буквы t в слове "cto" (которым ранее обозначали проценты). В скорописи буква t превратилась в черту (/), а затем и современный знак cto - c/o - %. Мы уже не узнаем, какая из версий правильная, однако знаком % пользуются в современном мире, и очень активно.
Слайд 4
Слово "процент" происходит от латинского "pro centum", что буквально означает "за сотню"
Слово "процент" происходит от латинского "pro centum", что буквально означает "за сотню"

Определение и основные типы задач на проценты
Тип 1: Находим процент (дробь) от числа.
Тип 2: Находим число по его проценту (дроби).
Тип 3: Находим процентное отношение двух чисел
Тип 4: Увеличиваем число на процент.
Тип 5: Уменьшаем число на процент
Тип 6: Задачи на простые проценты.
Тип 7: Задачи на сложные проценты.
Слайд 5Типы задач на проценты в ОГЭ
По содержанию задачи можно разбить на следующие
Типы задач на проценты в ОГЭ
По содержанию задачи можно разбить на следующие

Прикладные задачи : купля – продажа; оптимальный выбор; спрос – предложение
Финансовые задачи
Эти задания на использование приобретенных знаний и умений в практической деятельности и повседневной жизни, проверяющее умение решать прикладные задачи, в том числе социально-экономического и физического характера.
Слайд 6Под прикладной математикой обычно понимается тот раздел математики, в котором демонстрируется применение
Под прикладной математикой обычно понимается тот раздел математики, в котором демонстрируется применение

Прикладные задачи
1200×10:100=120 рублей - цена снижена на 10%
1200-120=1080 рублей со скидкой 10%
1080×15:100=162 рублей - цена снижена на 15%
1080-162=918 рублей со скидкой 15%
Ответ: 918 рублей
Задача № 1
В период распродажи магазин снижал цены дважды: в первый раз на 10 %, во второй — на 15 %. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 1200 рублей?
Решение.
По набранным бонусам покупатель имеет 7% скидку на приобретение бытовой техники , поэтому он заплатил за телевизор 32085
рублей. Найдите какова стоимость телевизора без скидки. Ответ выразите в рублях
Решение.
Задача № 2
100%-7%=93%=0.93 (Такую часть от всей цены заплатил покупатель)
32085 : (0.93) = 34500 рублей (Цена телевизора без скидки)
Ответ: 34500 рублей
Слайд 7Финансовые задачи
Объектом изучения являются любые финансово-кредитные операции, которые предполагают наличие ряда
Финансовые задачи
Объектом изучения являются любые финансово-кредитные операции, которые предполагают наличие ряда

денежные суммы;
временные параметры;
процентные ставки и некоторые другие дополнительные величины.
Каждая из перечисленных характеристик может быть представлена самым различным способом. На практике применяются 2 подхода к оценке процентного дохода – простые и сложные проценты.
Подоходный налог составляет 13% от заработной платы. После удержания налога на доходы Павел Витальевич получил 6090 рублей . Сколько рублей составляла его зарплата?
Решение.
6090 : 87*100 = 7000 рублей
Ответ: заработная плата – 7000 рублей
Задача № 2
Костя в начале 2009 года положил в банк 20000 рублей под 14% годовых. Сколько рублей было на счету Кости к концу 2010 года, если никаких операций со счёта за эти 2 года не проводилось?
Задача № 1
Решение.
(20000*14)/1000=2800 - сколько накопится процентов в первом году
(2800*14)/100=329- во втором году этот процент увеличится на 14%
329+2800=3192
3. Посчитаем итог:
20000+2800+3192=25992рубля
Ответ:25992рубля
Слайд 8Сами видите, решать задачи на проценты не так уж сложно. Если усвоить
Сами видите, решать задачи на проценты не так уж сложно. Если усвоить

В своей работе я показала, что знания о процентных вычислениях необходимы каждому человеку для жизни в современном обществе. Проценты применяются в различных сферах жизнедеятельности : в финансовой и экономической (банки), социальной (распределение населения), политической ( голосование), коммунальной (повышение и понижение стоимости электроэнергии и квартплаты), в товарных отраслях (распродажи, скидки), в научной (химия, физика – величина КПД).
Заключение
 Равносильность уравнений. 11 класс
Равносильность уравнений. 11 класс Прогрессии
Прогрессии Кривые второго порядка. Практика
Кривые второго порядка. Практика Эскизы кривых на плоскости, заданных параметрически
Эскизы кривых на плоскости, заданных параметрически Линейная алгебра просто! интерактивное учебное пособие
Линейная алгебра просто! интерактивное учебное пособие Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс Презентация на тему Симметрия. Осевая и центральная симметрии
Презентация на тему Симметрия. Осевая и центральная симметрии  Приведение дробей к общему знаменателю Молодых Наталья Андреевна Учитель математики средней школы № 3 г.Каменска- Уральского Св
Приведение дробей к общему знаменателю Молодых Наталья Андреевна Учитель математики средней школы № 3 г.Каменска- Уральского Св Двугранный угол. Перпендикулярность плоскостей
Двугранный угол. Перпендикулярность плоскостей Математический КВН
Математический КВН Преобразование графиков
Преобразование графиков Величины. Масса (1 класс)
Величины. Масса (1 класс)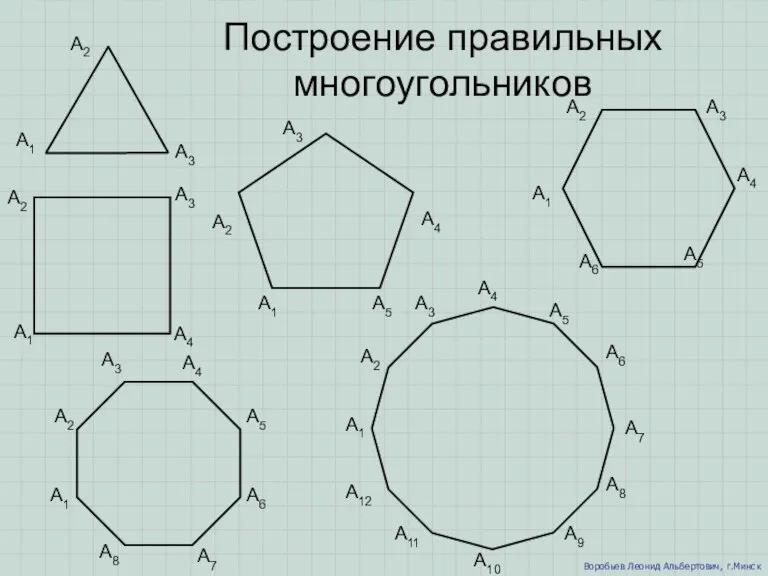 Построение правильных многоугольников
Построение правильных многоугольников Тест 3 по математике
Тест 3 по математике Рисунки из геометрических фигур
Рисунки из геометрических фигур Сравнение, сложение и вычитание дробей с разными знаменателями
Сравнение, сложение и вычитание дробей с разными знаменателями Сборник задач Во имя тех священных дней
Сборник задач Во имя тех священных дней Lek-AFK-Differentsialnye_uravnenia
Lek-AFK-Differentsialnye_uravnenia Геометрический смысл производной f '(x₀) = tg α = к
Геометрический смысл производной f '(x₀) = tg α = к Решение задач
Решение задач Квадратичная функция. Наглядно-методическое пособие. 9 класс
Квадратичная функция. Наглядно-методическое пособие. 9 класс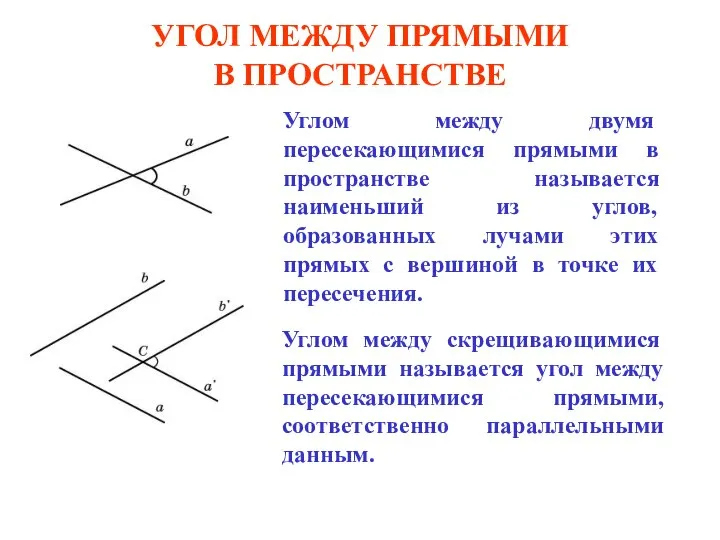 Угол между двумя прямыми в пространстве Вариант 2.ppt
Угол между двумя прямыми в пространстве Вариант 2.ppt Методы кластеризации
Методы кластеризации Без знаний дробей никто не может признаваться знающим арифметику
Без знаний дробей никто не может признаваться знающим арифметику Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ  Интерактивный тренажер Подобные слагаемые
Интерактивный тренажер Подобные слагаемые Площадь фигуры. Сравнение площадей
Площадь фигуры. Сравнение площадей